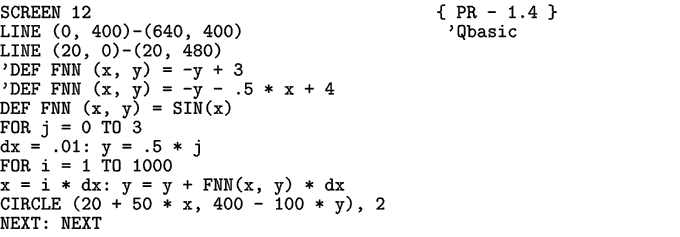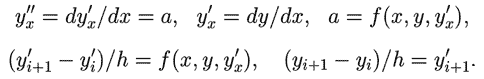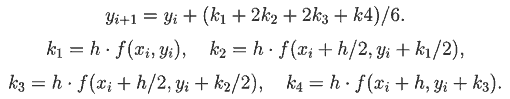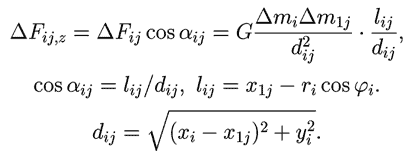ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ И ИНТЕГРАЛОВ
|
 |
Задача 1.
Исследуемый физический процесс описывается уравнением
x(t) = 3t3-3t2+4.
Определите первую и вторую производные функции
x = x(t) момент времени 2 с. Найдите интеграл данной функции в
интервале от 1 до 3 методом трапеций. Решите задачу аналитически
и сравните результаты. |
Алгоритм решения этой задачи АЛ-1 представлен ниже.
При уменьшении шага h получающиеся значения производной
и интеграла стремятся к некоторым предельным значениям,
которые совпадают с аналитически найденными значениями
производной y' и интеграла I функции (табл. 1).
Алгоритм АЛ - 1
ЗАДАТЬ ФУНКЦИЮ Funct:=t*t*t-t*t+3;
----------------------
НАЧАЛО ПРОГРАММЫ
t:=3; h:=0.001;
y1:=Funct(t-h); y2:=Funct(t); y3:=Funct(t+h);
ПЕЧАТЬ "Первая производная ", (y2-y1)/h
ПЕЧАТЬ "Вторая производная ", (y1-2*y2+y3)/(h*h)
a:=1; b:=3; t:=a; S:=0;
ПОВТОРЯТЬ{S:=S+0.5*(Funct(t)+Funct(t+h))*h; t:=t+h;}
ПОКА НЕ t>b;
ПЕЧАТЬ "Интеграл ", S
КОНЕЦ ПРОГРАММЫ
| 
|
Решением задачи является программа ПР-1. При уменьшении
шага точность вычислений обычно возрастает. Если же шаг очень мал,
то для нахождения интеграла приходится суммировать слишком большое
число слагаемых, что приводит к снижению точности. Точные значения
первых двух производных и интеграла приведены в нижней строчке табл. 1.
Программа ПР-1.

Таблица 1. Результаты вычислений
| Шаг Δx=h | x' | x'' | I |
| 0,2 | 21,120 | 30,000 | 42,200 |
| 0,1 | 22,530 | 30,000 | 48,177 |
| 0,01 | 23,850 | 30,000 | 42,584 |
| 0,001 | 23,985 | 30,000 | 42,000 |
| 0,0001 | 23,998 | 30,006 | 42,000 |
| 0,00001 | 24,000 | 30,268 | 42,001 |
| Точн. знач. | 24 | 30 | 42 |
 |
Задача 2.
Точка движется по закону:
x=3cos(t), y=2cos(3,7t+2). Вычислите координаты
x, y, проекции и модули скорости vx, vy, v и
ускорения ax, ay, a, нормальное aн
и тангенциальное aт ускорения в
моменты времени t=iΔt, i=1, 2, ...
|
Решением задачи является программа ПР-2.
Программа ПР-2.

 |
Задача 3.
Имеется неоднородная пластина, ограниченная функцией y=x1/2,
осью абсцисс, прямой x=2, плотность которой равна
ρ(x, y)=2+0,4y+0,2x2. Найдите момент инерции
пластины относительно оси Ox. |
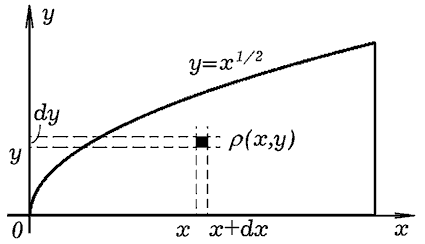
Рис. 1. К нахождению момента инерции пластины.
Вычисление момента инерции тела сводится к интегрированию по объему
и нахождению суммы элементарных моментов инерции. Разобьем тело (рис. 1)
на элементарные объемы dV=h·dx·dy массами dm=ρdV,
имеющими моменты инерции относительно оси Ox dI=y2dm.
Для нахождения суммы всех элементарных моментов инерции dI
организуют два вложенных цикла, в которых перебираются
и суммируются все dI (программа ПР-3).
| 
|
Программа ПР-3.

 |
Задача 4.
Решите дифференциальное уравнение первого порядка
y'x-f(x, y)=0 (например, y'x-sin(x)=0)
методом Эйлера. Получите семейство решений, соответствующих
различным начальным условиям y0=y(0).
|
Запишите уравнение в конечных разностях:
dy/dx = f(x,y), (yi+1-yi)/h=f(x,y),
где h=Δ x - шаг сетки по x. Отсюда следует:
yi+1=yi+f(x,y)h.
Чтобы численно решить уравнение, необходимо переменной y
присвоить значение y_0 = y(0), а затем в цикле рассчитать последующие
значения yi при i = 1, 2, ... в соответствии с приведенной
выше формулой. В программе ПР-4 (алгоритм АЛ - 2)
решается уравнение y'x-sin(x)=0 при трех различных
начальных условиях y(0) = 0, 0.5, 1. Получается семейство
из трех функций, отличающихся на постоянную величину.
| 
|
Алгоритм АЛ-2
ДЛЯ j:=0 ДО 3 ДЕЛАТЬ {-
dx:=0.01: y:=.5*j
ДЛЯ i:=1 ДО 1000 ДЕЛАТЬ {--
FNN:=sin(x); x:=i*dx; y:=y+FNN*dx;
ПОСТАВИТЬ ТОЧКУ С КООРДИНАТАМИ (x, y) --} -}
Используемая программа ПР-4 представлена ниже. Результаты ее использования
-- на рис. 2.
Программа ПР-4.
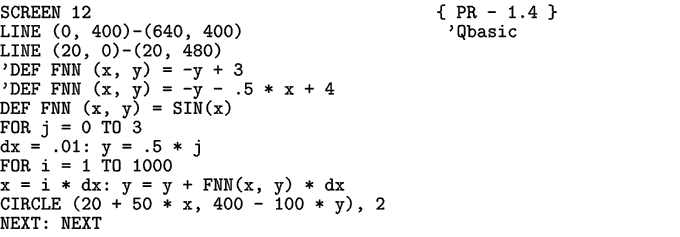
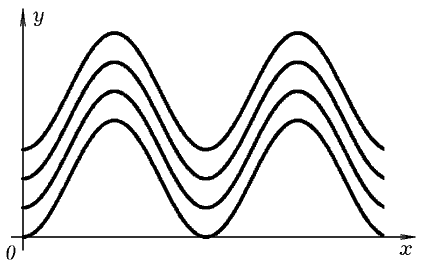
Рис. 2. Решение дифференциального уравнения
 |
Задача 5.
Тело ограничено поверхностями z1=f(x,y), z2=f(x,y).
Зависимость плотности от координат ρ=ρ(x,y,z) известна.
Методом Монте-Карло определите объем, массу и положение
центра масс тела.
|
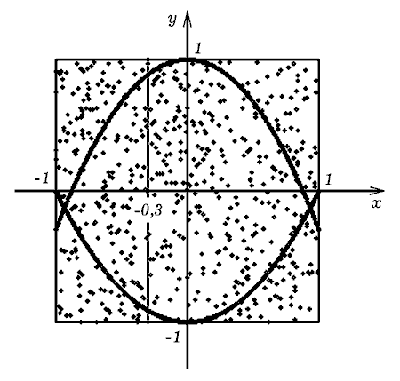
Рис. 3. К вычислению массы,
объема и координат центра масс тела
Пусть тело ограничено поверхностями
z1=1-1,3x2-y2,
z2=x2-1 (рис. 3). Плотность тела задается
соотношением: если x>-0,1, то ρ=3y + 5z + 10, иначе ρ=20.
Опишем вокруг тела куб, стороны которого перпендикулярны
осям координат и пересекают их в точках 1 и -1. Случайным
образом наполним куб большим количеством точек (106)
с координатами x, y, z. Подсчитаем количество точек nt, попавших
внутрь тела, тогда объем тела во столько раз меньше объема куба
(который равен 4 м3), во сколько раз число nt меньше
общего числа точек N.
Чтобы определить массу и координаты центра масс,
учтем, что на каждую точку приходится элементарный объем dV=4/N.
Поэтому будем умножать dV на плотность ρ в данной точке,
получающиеся элементарные массы складывать. Так мы найдем массу
тела msum. Для нахождения координат центра масс:
xsum:=xsum+rho*dV*x; ysum:=ysum+rho*dV*y;
zsum:=zsum+rho*dV*z; msum:=msum+rho*dV; end;
xc:=xsum/msum; yc:=ysum/msum; zc:=zsum/msum;
Решением задачи является программа ПР-5.
| 
|
Программа ПР-5.

 |
Задача 6.
Решите дифференциальное уравнение второго порядка
y''x-f(x,y,y'_x) = 0 (например,
y''x+y'x+1,2y - 5sin(x) = 0) методом Эйлера.
Начальные условия yx(0), y'x(0).
|
Дифференциальное уравнение второго порядка представимо в виде
системы двух дифференциальных уравнений первого порядка:
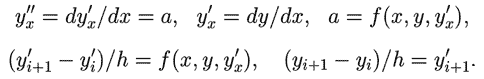
В программе ПР-6 создан цикл по i, в котором пересчитываются
значения yi, y'i и решается уравнение
y''x+y'x+1,2y-5sin(x)=0 (алгоритм АЛ-3).
Результаты решения -- на рис. 4.
y = 20: dx = 0.01 АЛ - 3
ДЛЯ i = 1 ДО 5000 ДЕЛАТЬ {- x = x + dx
pr2y = 5 * SIN(x) - .1 * pr1y - 1.2 * y
pr1y = pr1y + pr2y * dx; y = y + pr1y * dx
ПОСТАВИТЬ ТОЧКУ С КООРДИНАТАМИ (x, y) -}
| 
|
Программа ПР-6.

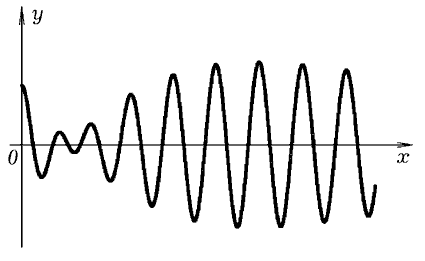
Рис. 4. Решение дифференциального уравнения
 |
Задача 7.
Решите дифференциальное уравнение первого порядка
вида y'x-f(x,y) = 0 методом Рунге - Кутта
четвертого порядка.
|
Сущность метода Рунге - Кутта четвертого порядка
выражается следующими формулами:
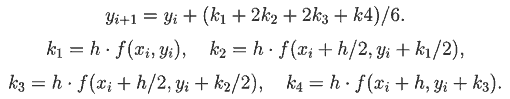
Организуем цикл по i, в котором вычисляются значения функции
y(x) по этой схеме. Например, для решения уравнения
y'x-2sin(x)+0.5/y=0 используется
алгоритм АЛ-4. | 
|
АЛ - 4
ЗАДАТЬ ФУНКЦИЮ FNN (x, y) = 2 * SIN(x) + .5 / y
--------------------------------
y = 1: dx = .01
ДЛЯ i = 1 ДО 1500 ДЕЛАТЬ {-
x = i * dx; k1 = FNN(x, y);
k2 = FNN(x + dx / 2, y + dx * k1 / 2)
k3 = FNN(x + dx / 2, y + dx * k1 / 2)
k4 = FNN(x + dx, y + k3)
y = y + dx / 6 * (k1 + 2 * k2 + 2 * k3 + k4)
ПОСТАВИТЬ ТОЧКУ С КООРДИНАТАМИ (x, y) -}
Этот алгоритм реализован в программе ПР-7. Результат -- на рис. 5.
Программа ПР-7.

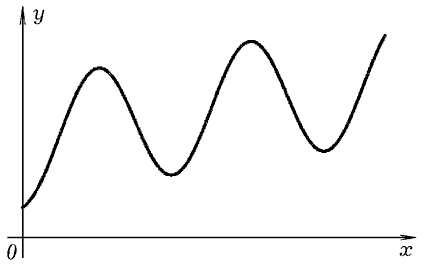
Рис. 5. Решение диффуравнения методом Рунге - Кутта
 |
Задача 8.
Решите дифференциальное уравнение второго порядка
y''x-f(x, y, y'x)=0 методом Рунге - Кутта
четвертого порядка. Начальные условия yx(0), y'x(0).
|
Записывают данное уравнение в виде системы двух дифференциальных уравнений
первого порядка и используют рассмотренную выше схему Рунге - Кутта.
Используется алгоритм АЛ-5.
Алгоритм АЛ-5
ЗАДАТЬ ФУНКЦИЮ FNN1 (x, y, pr1) = SIN(x) -
.25 * pr1 - .9 * SIN(y)
--------------------------------
y = 2: v = 0: dx = .01
ДЛЯ i = 1 ДО 8000 ДЕЛАТЬ {-
x = i * dx: k1 = FNN1(x, y, pr1)
k2 = FNN1(x + dx / 2, y, pr1 + dx * k1 / 2)
k3 = FNN1(x + dx / 2, y, pr1 + dx * k2 / 2)
k4 = FNN1(x + dx, y, pr1 + k3)
pr1 = pr1 + dx / 6 * (k1 + 2 * k2 + 2 * k3 + k4)
y = y + pr1 * dx
ПОСТАВИТЬ ТОЧКУ С КООРДИНАТАМИ (x, y) -}
Программа ПР-8 позволяет решить уравнение
y''x+0,25y'x + 0,9sin(y)=sin(x). Результаты
представлены на рис. 6. | 
|
Программа ПР-8.

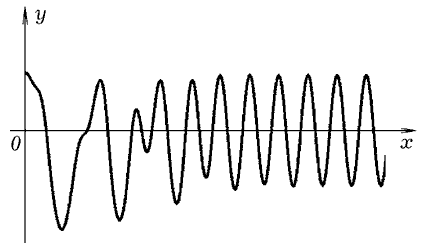
Рис. 6. Решение диффуравнения методом Рунге - Кутта
 |
Задача 9.
Определите силу гравитационного притяжения, действующую
со стороны шарообразного тела радиуса R, на материальную точку
массой m, находящуюся на расстоянии z' от центра. Плотность шара
ρ(r)=100/r, где r - расстояние от его центра.
|
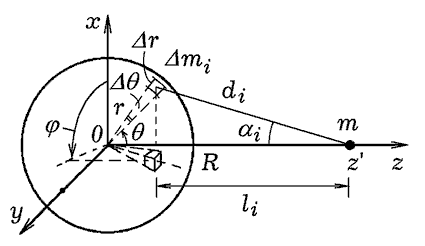
Рис. 7. К расчету взаимодействия шара и точки
Распределение плотности шарообразного тела, а значит, и его
гравитационное поле обладают центральной симметрией, поэтому
задачу следует решать в сферической системе координат (рис. 7).
Результирующая сила может быть найдена по формулам:
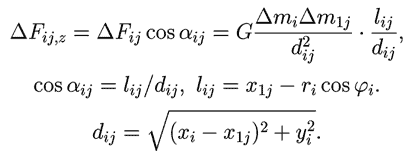
где i = 1, 2, ... , n, n - число элементарных масс Δmi,
li=z'-r cosθi. Программа ПР-9 для
расчета искомой силы F содержит вложенные друг в друга
цикл по r, цикл по φ и цикл по θ, позволяющие перебрать все
элементарные массы тела, рассчитать и просуммировать проекции сил
ΔF на ось Oz.
| 
|
Программа ПР-9.

 |
Задача 10.
Определите силу гравитационного притяжения, действующую между
неоднородным диском радиусом R, толщиной h и однородным
стержнем массой m1, концы которого имеют координаты a и b>R.
Зависимость плотности диска от координаты: ρ(r)=100/r, где r -
расстояние от его центра O. |
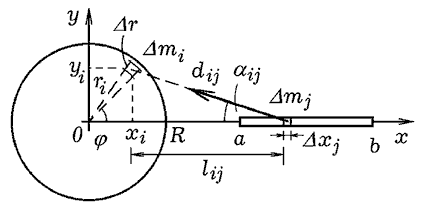
Рис. 8. К расчету взаимодействия диска и стержня
Распределение массы обладает осевой симметрией. Будем
использовать полярную и декартовую системы координат (рис. 8).
Разобьем диск на n элементарных объемов
ΔV=rh ΔφΔr с координатами
xi=r cos(φ), yi=r sin(φ) и массами
Δm=ρ(r)ΔV=ρ(r) rhΔφΔr.
Стержень рассмотрим как k элементарных масс
Δm1=m1/k с координатами
x1j=a+jΔx, где j = 1, 2, ... , k.
Расстояние между Δmi и Δm1j равно
dij=[(xi - x1j)2 +
yi2]0,5.
Проекция силы ΔFij на ось Oz равна:
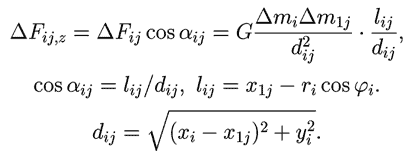
| 
|
В используемой программе ПР-10 перебираются все элементарные
массы Δmi и Δm1i обоих тел,
определяются и суммируются проекции сил притяжения на ось Oz.
Программа ПР-10.

Тексты программ находятся в zip-архиве,
файл gl-1.pas.
ВВЕРХ
Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс].
- Глазов: ГГПИ, 2012 //
Web-site http://maier-rv.glazov.net .
|