Задача 1. Размножение насекомых на изолированном острове описывается квадратичным отображением xi+1=axi(1-xi). Изучите поведение этой функции в зависимости от параметра a, изменяющегося в интервале от 0 до 4. Постройте график x=x(r) и найдите точки бифуркации, в которых происходит расщепление пути эволюции системы и наступает динамический хаос.

Численность насекомых Ni+1 в (i+1)-м поколении с одной стороны пропорциональна числу насекомых Ni в предыдущем i-м поколении. С другой стороны, с ростом Ni насекомые начинают испытывать нехватку энергетического ресурса (еды), и их коэффициент размножения уменьшается. При достижении числа насекомых Ni своего предела A коэффициент размножения уменьшается до 0. Получаем уравнение:

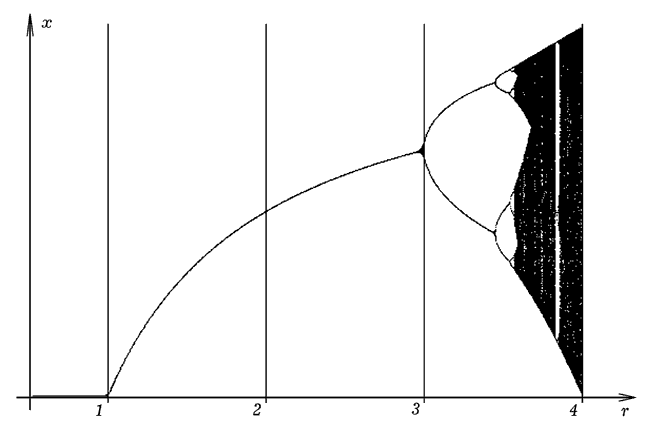
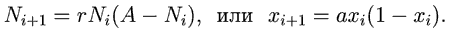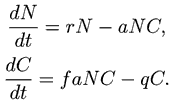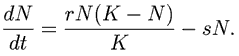Напишем программу ПР-1, вычисляющую по 100-1000 значений x_i при различных значениях параметра a, который изменяется от 0 до 4 и выводит результаты на экран в графическом виде. Результат ее работы представлен на рис. 1. Видно, что пока a меньше 3, каждому значению параметра a соответствует одно значение x. Дальнейшее увеличение a приводит к каскаду бифуркаций удвоения периода: сначала одному значению a отвечают два значения x, затем 4, затем 8 и т.д. Последовательность бифуркаций, начинаясь слева, переходит в хаос справа, которому соответствует уже не непрерывная линия, а фрактальное множество точек. Полосы хаоса перемежаются с "окнами периодичности".

Программа ПР-1.

Рис. 1. Квадратичное отображение.

Задача 2. На изолированном острове имеется популяция волков (хищников) и популяция зайцев (жертв). Встречаясь с зайцем, волк съедает его, при этом число зайцев уменьшается, а популяция волков растет. Без пищи волки вымирают от голода. Изучите динамику хищника и жертвы на компьютере.

Численность популяции зайцев и волков обозначим через N и C. Быстрота увеличения числа зайцев dN/dt зависит от их числа N, коэффициента рождаемости r, а также частоты встреч волков и зайцев, которая пропорциональна NC. Скорость изменения числа волков dC/dt определяется их количеством C, коэффициентом смертности q, а также частотой встречи с зайцами, пропорциональной NC: Ниже представлена программа ПР - 2, позволяющая вычислить численность популяции волков и зайцев в последовательные моменты времени и строящая фазовую кривую системы. Результат вычислений - на рис. 2.

Программа ПР-2.

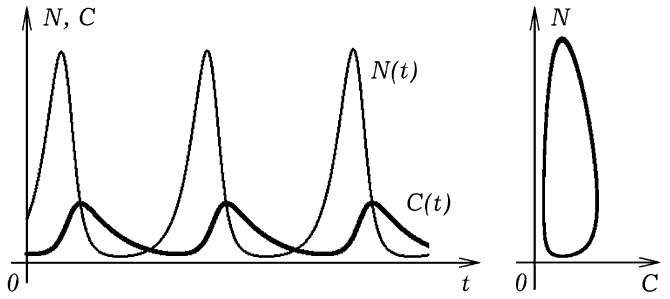
Рис. 2. Динамика популяции волков и зайцев.

Задача 3. Имеется популяция животных одного вида. Известен коэффициент рождаемости r, коэффициент смертности s и максимально возможная численность животных K. Как изменяется численность популяции с течением времени, если смертность на некоторое время резко увеличивается (например, вследствие эпидемии).

Быстрота увеличения численности животных dN/dt пропорциональна их количеству N. При этом имеет место внутривидовая конкуренция, состоящая в использовании энергетического ресурса одним животным, что снижает доступность этого ресурса для другого животного того же вида. Это приводит к тому, что с ростом численности N коэффициент рождаемости уменьшается, а когда N приближается к максимально возможному числу K, рождаемость падает до 0. Чтобы учесть уменьшение числа животных N вследствие смертности, вводят слагаемое -sN, где s - коэффициент смертности. Получается: Для численного решения этого уравнения используется программа ПР-3. В интервале [t1;t2] смертность увеличивается в 5 раз. Результат моделирования - на рис. 3.

Программа ПР-3.

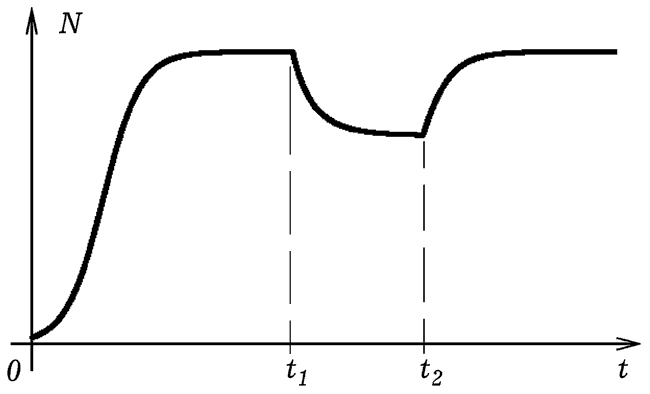
Рис. 3. Зависимость численности популяции от времени.

Задача 4. В море совместно существуют рыбы и акулы. Средняя продолжительность жизни, время через которое рыбы и акулы дают новое потомство, их скорость движения известны. Необходимо создать дискретную модель этой биологической системы, изучить изменения численности рыб и акул с течением времени при различных ее параметрах и начальных условиях.

Программа должна содержать цикл по времени t; каждая итерация цикла приводит к увеличению t на 1 условную единицу времени (УЕВ). Модель двумерная и дискретная; поверхность моря разбита на квадратные ячейки длиной 1 условная единица длины (УЕД). Каждой ячейке с координатами i и j отвечает элемент массива xi,j. Ячейка может быть пустой (xi,j=0), либо содержать рыбу (xi,j больше 0), либо содержать акулу xi,j меньше 0. Абсолютное значение xi,j равно возрасту рыбы или акулы. Если xi,j=3, значит ячейка содержит рыбу возрастом 3 УЕВ. Если xi,j=-5, значит в этой ячейке акула возрастом 5 УЕВ.

Допустим, продолжительность жизни рыб и акул равны live_r=8, live_a=12 УЕВ. Каждая рыба (акула) через rogd_r=2 УЕВ (rogd_a=3 УЕВ) может родить одну рыбу (акулу), возраст которой равен 0. Это происходит, когда соседняя случайным образом выбранная ячейка не занята рыбой (акулой). В противном случае (ячейка занята) рождения не происходит из-за перенаселенности. С каждым оборотом цикла возраст всех рыб и акул увеличивается на 1 УЕВ. Когда возраст рыбы (акулы) превышает среднюю продолжительность жизни, то рыба (акула) умирает от старости. Рыбы питаются водорослями и червями, а акулы поедают рыб. Если для какой-то ячейки (i,j), занятой рыбой, количество соседних ячеек, занятых рыбами, больше 6, то эта рыба умирает от перенаселения (недостатка пищи): x[i,j]=0. Если акула не ела в течение t_gol=5, то она умирает от голода. За 1 УЕВ акула может переместиться в одну из 8 соседних ячеек (при этом ее координаты i и j изменяются на 1), либо остатья на месте. Если при перемещении акула попадает в ячейку, занятую рыбой, то она съедает ее. При этом переменная gol[i,j] обнуляется. На каждом временном шаге, когда акула не съела рыбу, величина gol[i,j] увеличивается на 1. Рыба движется медленно и перемещается в соседнюю ячейку за 8 УЕВ.

Программа ПР-4.

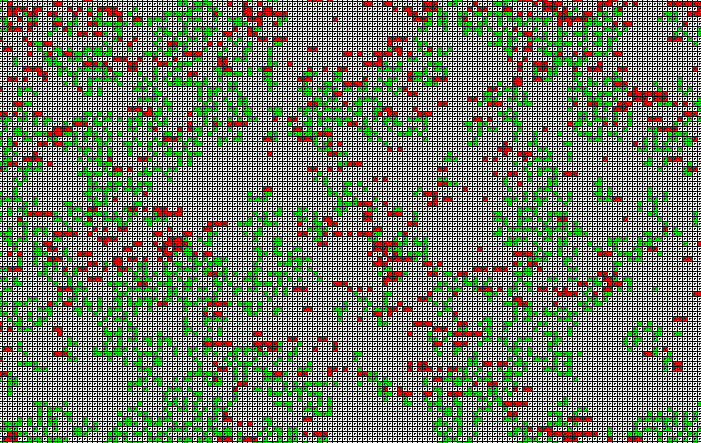
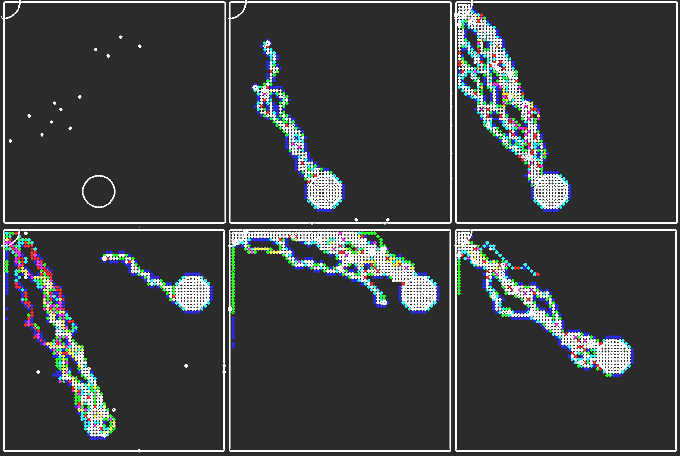
Рис. 4. Дискретная модель совместного существования рыб и акул.

Используется программа ПР-4. Сначала случайным образом задается расположение заданного количества рыб и акул и их возраст. Основнм является цикл по времени t Repeat ... until KeyPressed;. В нем рассчитывается: 1) возраст каждой рыбы и акулы; 2) перемещение рыб и акул; 3) рождение рыб и акул; 4) смерть рыб от перенаселенности; 5) смерть от голода. Для вывода изображения на экран используется процедура Draw. Если ее закоментировать и активизировать следующие несколько строчек программы, то на экране будет рисоваться график зависимости численности акул от времени.

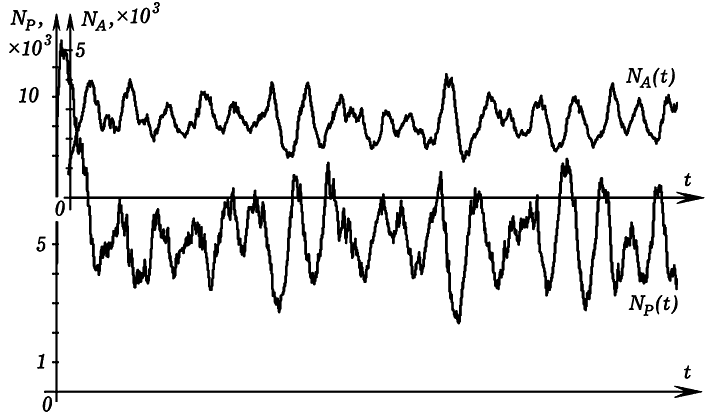
Рис. 5. Колебания численности рыб и акул с течением времени.

При запуске программы ПР-4 на экране появляется двумерная сетка (рис. 4), по которой перемещаются рыбы (зеленые клетки) и акулы (красные клетки). Белый цвет означает, что в ячейке нет ни рыбы, ни акулы. Компьютерная модель позволяет исследовать совместное сосуществование рыб и акул в одной акватории при различных параметрах этой системы. Программа позволяет промоделировать ситуацию, когда акулы, зайдя в область i от 0 до 20, умирают (мелководье или зона охоты). Если уменьшать продолжительность жизни акул, длительность их существования без пищи, увеличивать период появления потомства, то можно добиться того, что акулы вымрут, а рыбы останутся. Можно подобрать такие параметры модели, при которых будут происходить колебания численности рыб и акул (рис. 5). Размножение рыб приводит к росту численности акул, эти процессы инерционны, система проскакивает положение равновесия. Когда акул становится слишком много, они поедают большую часть рыб, им не хватает пищи и часть из них умирают от голода. Уменьшение численности акул приводит к увеличению количества рыб.

Задача 5. Имеется муравейник, из которого выползают муравьи. Двигаясь случайным образом, они находят пищу, а затем несут ее частицы в свой дом, оставляя феромоновый след. Этот след позволяет другим муравьям найти дорогу к источнику пищи, даже если он находится за препятствием. Необходимо, используя мультиагентный подход, промоделировать поведение колонии муравьев.

Ученые установили, что сначала муравьи совершают случайные перемещения и при нахождении пищи, возвращаются в свою колонию, отмечая свой путь особыми веществами -- феромонами. Когда другие муравьи натыкаются на феромоновые тропы, то они с большой вероятностью движутся по ним. Дойдя до источника питания, эти муравьи возвращаются в колонию также, "поливая" свой путь феромонами. С течением времени феромоны испаряются, вероятность выбора муравьем данного пути уменьшается. Более длинный путь требует большего времени для прохождения от муравейника до пищи и обратно, поэтому при тех же условиях феромоновый след испарится сильнее. По короткому пути прохождение будет быстрым, плотность феромонов высокой. Если какой-либо муравей нашел более короткий путь до источника пищи, то другие муравьи вероятнее всего пойдут по его следу, увеличат концентрацию феромонов, что сделает его еще более привлекательным. При этом длинный путь прервется, феромоновый след испарится.

В нашей модели роль муравья будет выполнять программный агент, который характеризуется двумя координатами X и Y состоянием S. Разобъем горизонтальную поверхность на ячейки, каждая из которых характеризуется целочисленными величинами x и y, принимающими значения 1, 2, 3, ..., L. Каждый k-ый муравей (k= 1, 2, ..., N) имеет координаты x_k и y_k. Муравьи могут находится в одном из трех состояниях (S=1, 2, 3). Находясь в состоянии S=1 (поиск), муравьи случайным образом перемещаются по поверхности земли, ища пищу. Наткнувшись на пищу, муравей переходит в состояние S=2 (возврат в муравейник с пищей). При этом он перемещается в сторону муравейника, оставляя за собой феромоновый след. После того, как он достиг муравейника и отдал пищу, муравей переходит в состояние 3 (движение по следу в сторону пищи). Если другой муравей в состоянии поиска S=1 наткнется на феромоновый след, то он также перейдет в состояние 3 и будет двигаться по следу от муравейника. Феромоны с течением времени испаряются, след прерывается. Если муравей, находящийся в состоянии 3, движется по "тропинке" к пище и натыкается на разрыв следа либо теряет его, то он переходит в состояние S=1 (поиск). При этом система не имеет централизованного управления, обмен локальной информацией осуществляется только между отдельными агентами посредством феромона, используется мультиагентный подход.

Программа ПР-5.

Рис. 6. Термиты ищут дорогу к источникам пищи.

Рис. 7. Термиты ищут дорогу к источнику пищи за препятствием.

Решение данной задачи позволило разработать муравьиный алгоритм, который является эффективным способом нахождения оптимальных маршрутов на графах. В его основе лежит моделирование поведения колонии муравьев, каждый из которых моделируется программным агентом, работающим в соответствии с некоторыми простыми правилами. Установлено, что с ростом размерности решаемых задач оптимизации эффективность муравьиных алгоритмов повышается. Они применимы к динамически изменяющимся сетям, т.к. за счет испарения феромона происходит перестройка оптимального маршрута.

Тексты программ находятся в zip-архиве, файл gl-11.pas.

Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net .