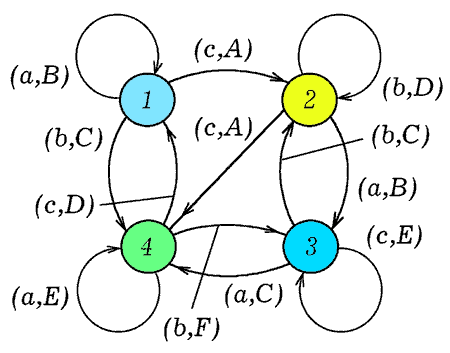
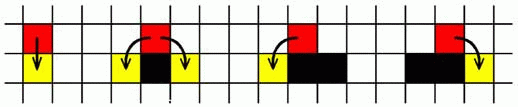
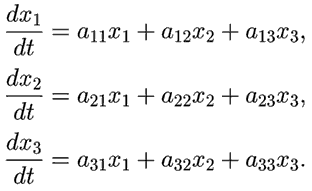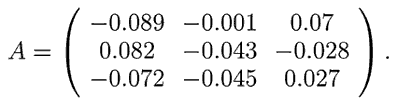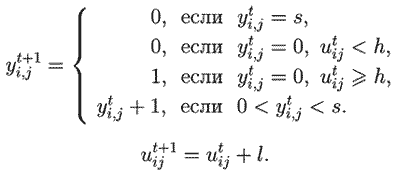Рис. 1. Диаграмма Мура автомата с четырьмя состояниями.
Программа ПР-1.
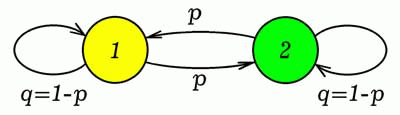
Рис. 2. Диаграмма Мура автомата с двумя состояниями.
Изначально автомат не обучен. Пусть он может совершить 100 различных операций с равными вероятностями, тогда вероятность правильного действия p=0.01. Программа ПР-2, моделирующая ученика, содержит цикл, в котором выбор каждой операции осуществляется с помощью генератора случайных чисел. Если случайное число x, находящееся в интервале [0;1], меньше p, то АМУ совершает правильное действие, если нет - делает ошибку. Процесс обучения приводит к изменению матрицы вероятностей: вероятность правильного выбора p увеличивается на a*q, где a - коэффициент научения, а вероятность ошибки уменьшается на ту же величину. Уровень знаний Z будем считать равным вероятности p правильного перехода. Чтобы учесть забывание необходимо на каждом временном шаге уменьшать p на g*p (g - коэффициент забывания) и на такую же величину увеличивать q: p:=p-g*p; q:=q+g*p; {забывание}
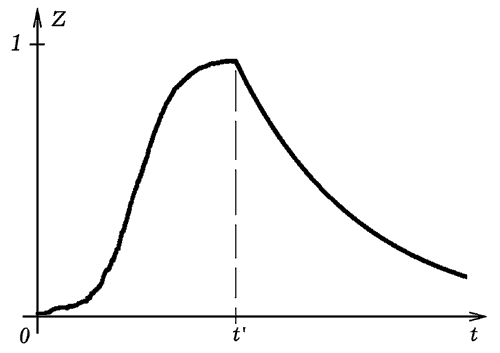
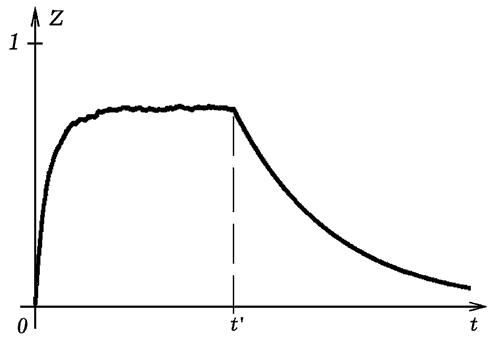
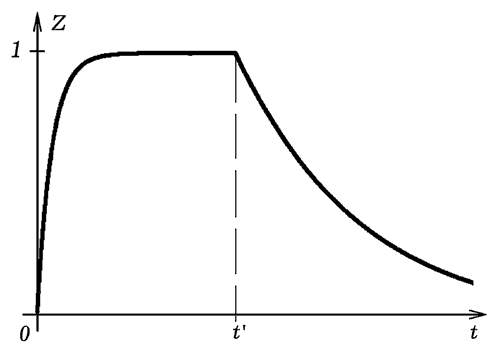
Программа позволяет промоделировать ситуации: Обучение с поощрением: при выполнении правильного действия ученика "поощряют", пересчитывая вероятности p и q. Так как сначала ученик ошибается гораздо чаще (q превосходит p), то сначала обучение происходит медленно (рис. 2). Зато по мере увеличения "знаний" вероятность совершения правильного действия растет. Акты обучения происходят все чаще, вероятность p увеличивается до 1. Программа содержит строку: If (x<p)and(t<4000) then begin p:=p+a*q; q:=q-a*q; end; Обучение с наказанием: в случае ошибки ученика "наказывают", подсказывая ему правильный ответ, что приводит к росту p и уменьшению q. Сначала ученик ошибается часто, поэтому уровень его "знаний" быстро растет, вероятность ошибки q падает (рис. 3). Акты обучения происходя реже, вероятность правильного действия не достигает 1 (за счет забывания). Программа содержит строку: If (x>p)and(t<4000) then begin p:=p+a*q; q:=q-a*q; end; Обучение с поощрением и наказанием: при правильном ответе ученика поощряют, а при неправильном - наказывают, подсказывая правильный ответ. В обоих случаях вероятность правильного действия p растет, а вероятность ошибки снижается. За счет того, что при любом действии учащегося его учат, уровень знаний быстро растет и достигает 1 (рис. 4). Программа содержит строку: If t<4000 then begin p:=p+a*q; q:=q-a*q; end; Программа ПР-2.
Рис. 3. Обучение с поощрением.
Рис. 4. Обучение с наказанием.
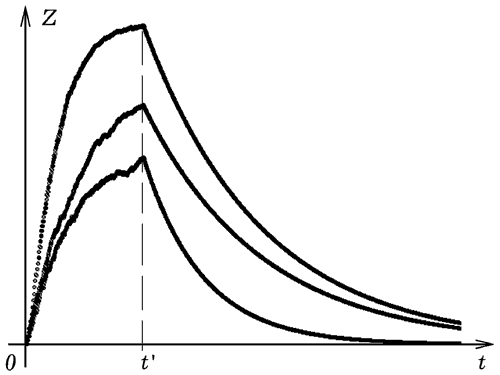
Рис. 5. Обучение с поощрением и наказанием. Рассмотрим другой вариант решения задачи (программа ПР-3). В процедуре Uchenik случайным образом (исходя из матрицы вероятностей) производится переход в следующее состояние. В процедуре Obuchenie осуществляется пересчет вероятностей переходов из одного состояния в другое, в процедуре Zabyvan различие между вероятностями правильных и неправильных переходов уменьшается. На экране получаются графики зависимости уровня знаний от времени при различных коэффициентах научения и забывания (рис. 5). Программа ПР-3.
Рис. 6. Кривые обучения.
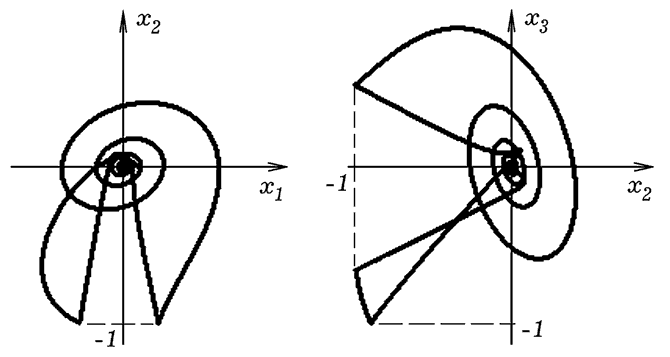
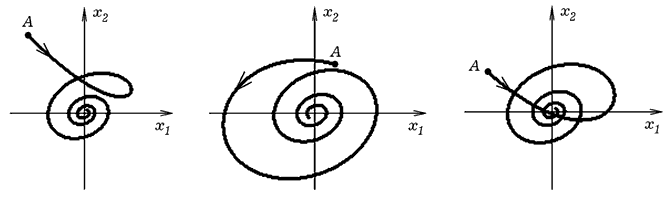
Программа ПР - 4 для нахождения коэффициентов ai,j, определяющих работы гомеостата, работает так. Значения ai,j и xj задаются случайным образом. Вычисляются скорости v1, v2, v3 и координаты x1, x2, x3 в последовательные моменты времени. Если модуль хотя бы одной из координат превысил 1, то коэффициенты ai,j изменяются случайным образом. Так продолжается до тех пор, пока система не вернется в положение равновесия (0,0,0). Найденные значения коэффициентов ai,j печатаются в файл. На рис. 7 показана фазовый портрет гомеостата на этпе подбора коэффициентов. Программа ПР-4.
Рис. 7. Подбор параметров гомеостата. В результате работы программы ПР-4 рассчитываются коэффициенты ai,j, при которых гомеостат находится в положении равновесия (0,0,0). Эта задача имеет несколько решений. Допустим, получились следующие значения:
После того, как найдены оптимальные параметры гомеостата, можно исследовать, как ведет себя гомеостат при выводе его из положения равновесия. В программе ПР-5, содержащей оптимальные параметры, случайным образом задаются начальные координаты x1, x2, x3 из интервала [-0,9; 0,9] и рассчитывается "поведение" гомеостата в последующие моменты времени. Во всех случаях гомеостат возвращается в положение равновесия (рис. 8). Программа ПР-5.
Рис. 8. Функционирование гомеостата.
Программа ПР-6.
Рассмотрим обобщенную модель Винера - Розенблюта. Пусть состояние каждого элемента в момент t описывается фазой yi,jt, и концентрацией активатора ui,jt. Если элемент находится в покое, то будем считать, что yi,jt=0. Если вследствие близости возбужденных элементов концентрация активатора ui,jt достигает порогового значения h, то элемент возбуждается и переходит в состояние 1. Затем на следующем шаге он переключается в состояние 2, затем - в состояние 3 и т.д., оставаясь при этом возбужденным. Достигнув состояния r, элемент переходит в состояние рефрактерности. Через s (s>r) шагов после возбуждения элемент возвращается в состояние покоя:
Будем считать, что при переходе из состояния s в состояние покоя 0 концентрация активатора становится равной 0. При наличии соседнего элемента, находящегося в возбужденном состоянии, она увеличивается на 1. Можно ограничиться учетом ближайших восьми соседних элементов. Используется программа ПР-7, получающиеся результаты представлены на рис. 9 и 10. Программа ПР-7.
Рис. 9. Однорукавная и двурукавная автоволны.
Рис. 10. Подавление низкочастотного источника высокочастотным. Дифракция автоволн.
Рис. 11. Струя жидкости, наполняющая сосуд.
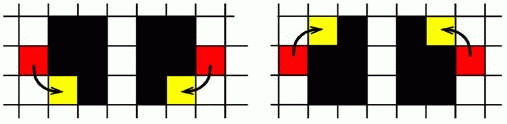
Рис. 12. Опускание частиц жидкости. Чтобы промоделировать опускание частиц жидкости под действием силы тяжести (рис. 12), должны выполняться следующие правила:
Если a[i,j]=1 (жидкость), то
1. Если a[i,j-1]=0, то a[i,j-1]:=1, a[i,j]:=0;
2. Если a[i,j]=1 и a[i-1,j-1]=0 и a[i+1,j-1]=0,
то a[i,j]:=0 и с вероятностью 0,5
a[i-1,j-1]:=1 или a[i+1,j-1]:=1;
3. Если a[i-1,j-1]=0 и a[i+1,j-1]=1,
то a[i-1,j-1]:=1, a[i,j]:=0;
4. Если a[i+1,j-1]=0 и a[i-1,j-1]=1,
то a[i+1,j-1]:=1, a[i,j]:=0;
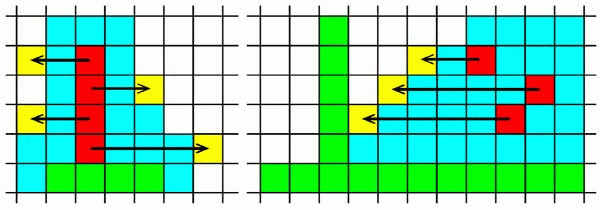
Рис. 13. Сглаживание "неровностей" струи. На частицы жидкости, находящиеся вблизи ее поверхности, действуют силы поверхностного натяжения, что приводит к "сглаживанию" неровностей. Чтобы учесть этот эффект, для клеточных автоматов должны выполняться правила (рис. 13):
Если a[i,j]*a[i+1,j]*a[i+2,j-1]=1 и a[i+1,j-1]=0, то
a[i+1,j-1]:=1, a[i,j]:=0;
Если a[i,j]*a[i-1,j]*a[i-2,j-1]=1 и a[i-1,j-1]=0), то
a[i-1,j-1]:=1, a[i,j]:=0;
Если a[i,j]*a[i+1,j]*a[i+2,j+1]=1 и a[i+1,j+1]=0, то
a[i+1,j+1]:=1, a[i,j]:=0;
Если a[i,j]*a[i-1,j]*a[i-2,j+1]=1 и a[i-1,j+1]=0, то
a[i-1,j+1]:=1, a[i,j]:=0;
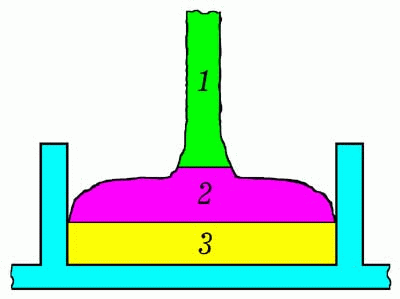
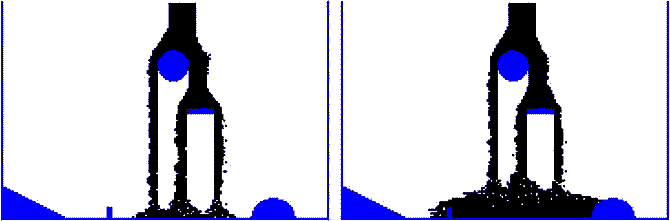
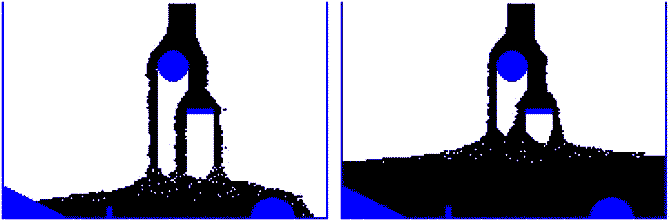
Рис. 14. Растекание струи. Когда вертикальная струя жидкости падает на горизонтальную поверхность, то направление движения частиц жидкости изменяется на 90 градусов. При этом жидкость растекается по поверхности так, что частицы жидкости из средней части струи перемещаются в горизонтальном направлении вправо или влево. Это можно промоделировать следующим образом (рис. 14): Если a[i,j]=1 и (a[i,j-1]=-2 или a[i,j-2]=-2 или a[i,j-3]=-2 или a[i,j-4]=-2), то с вероятностью 0,1 смещать элемент по горизонтали влево или вправо до первой пустой клетки; Аналогичное правило должно выполняться при наполнении сосуда. Компьютер подсчитывает толщину области 3, частицы которой полностью заполняют горизонтальные строки двумерной матрицы ai,j между стенками сосуда. Растекание жидкости в области 2, которая содержит пустые клетки с ai,j=0, моделируется так: случайно выбирается наполненная жидкостью клетка (ai,j=1) и смещается по горизонтали влево или вправо (случайный выбор) до ближайшей пустой клетки, после чего эти клетки меняются местами (рис. 14). Предложенный алгоритм реализован в программе ПР-8, представленной ниже. Результаты моделирования заполнения жидкостью сосуда с препятствиями представлены на рис. 15, 16 и 17. Программа ПР-8.
Рис. 15. Наполнение сосуда вязкой жидкостью.
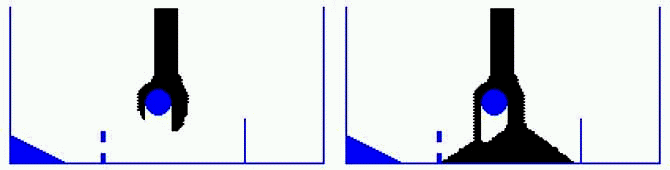
Рис. 16. Наполнение сосуда вязкой жидкостью (увеличено).
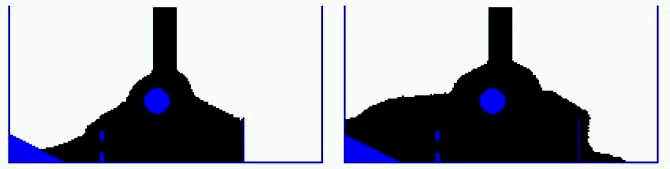
Рис. 17. Наполнение сосуда вязкой жидкостью (t=40, 80, 160 и 240). Тексты программ находятся в zip-архиве, файл gl-12.pas. ВВЕРХ
Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net . |