Задача 1. На базе формального нейрона создайте компьютерную модель однослойного персептрона, который бы осуществлял распознавание образов и классификацию объектов на два класса.

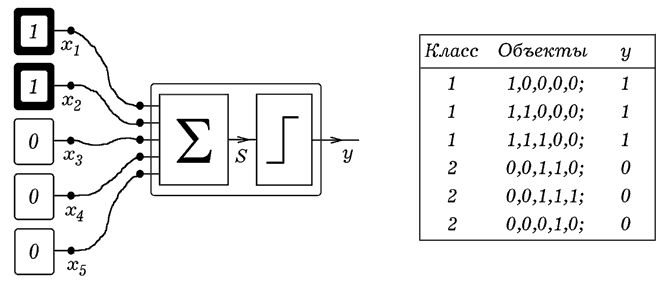
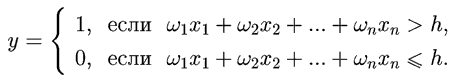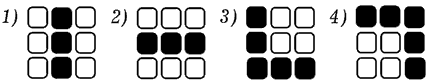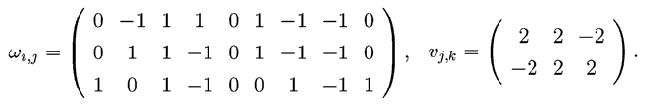Рис. 1. Однослойный персептрон на базе нейрона

Под формальным нейроном понимают гипотетический автомат с n входами x1, x2,..., xn и одним выходом y, характеризующийся порогом h и весами w1, w2... wn. Он состоит из суммирующего и порогового элементов. Его выход возбужден (y = 1), когда сумма всех весов возбужденных входов превышает порог срабатывания: w1x1+w2x2 + ... + wnxn> h. В противном случае выход не возбужден (y = 0). Это можно записать так:

Если вес i-го входа положительный (w_i>0), то вход - возбуждающий, если отрицательный (w_i<0), - вход тормозящий.

Так как выход искусственного нейрона может находиться в двух состояниях, то он может разделять объекты только на два класса. Чтобы симмитировать работу нейрона (рис. 1), достаточно найти взвешенную сумму его входов и использовать оператор условного перехода. Так работает программа ПР-1: формальному нейрону последовательно предъявляются 6 объектов, образующих два класса: K₁={10000, 11000, 11100} и K₂={00111, 00111, 00010}. Вес входов подобран так: w_i=(1,1,1,-1,-1), порог срабатывания равен h=0,2. После запуска программы получаем:

Объект 1: S=  1.0; y= 1
Объект 2: S=  2.0; y= 1
Объект 3: S=  3.0; y= 1
Объект 4: S= -1.0; y= 0
Объект 5: S= -1.0; y= 0
Объект 6: S= -1.0; y= 0

Программа ПР-1.

Задача 2. Рассчитайте нейросеть с 2 входами и 4 нейронами (рис. 2). При подаче на вход сигналов o[1]={00}, o[2]={01}, o[3]={10}, o[4]={11} на выходах нейронов должно появиться y[1,j]={1000}, y[2,j]={0100}, y[3,j]={0010}, y[4,j]={0001}, то есть соответствующий нейрон должен быть возбужден.

Рис. 2. Схема нейросети с 2 входами и 4 нейронами.

Написать программу, моделирующую работу этой нейросети, несложно. Вес синапсов и порог срабатывания нейрона задаются матрицами: w[1,j]=(-1, -2, 1, 1), w[2,j]=(-1, 1, -2, 1), h[j]= (-0.5, 0, 0, 1.5). Решением задачи является программа ПР-2.

Программа ПР-2.

Задача 3. Промоделируйте персептрон (двухслойную нейросеть) с 8 входами (сенсорами), 4 ассоциативными элементами и 2 реагирующими элементами (рис. 3). При предъявлении объектов o[1]={11110000}, o[2]={0000 1111}, o[3]={00111100}, o[4]={11000011} на выходах персептрона должны появиться сигналы y[1,j] = {00}, y[2,j] = {01}, y[3,j] ={10}, y[4,j] ={11}.

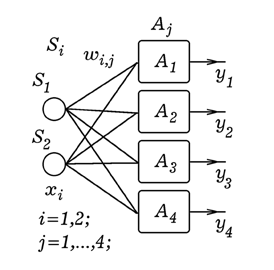
Рис. 3. Схема персептрона с 8 входами.

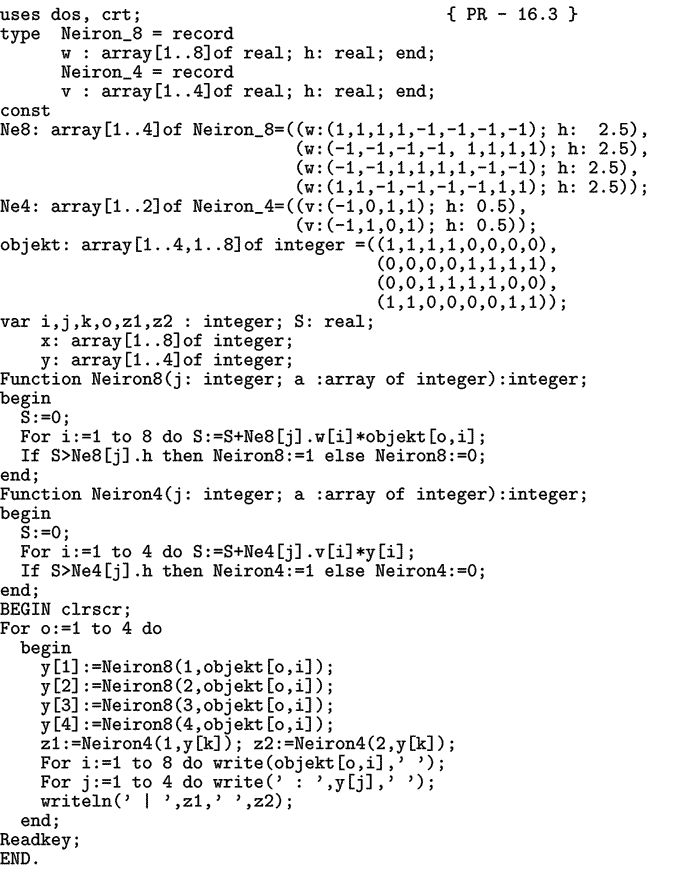
Программа ПР-3, моделирующая работу этой нейросети, представлена ниже. Для задания параметров нейронов используются записи. Датчикам нейросети последовательно предъявляются четыре объекта, которые распознаются, то есть классифицируются на четыре класса.

Программа ПР-3.

Задача 4. Имеется однослойная нейросеть с 9 входами и 4 нейронами. Напишите программу, вычисляющую веса w так, чтобы сеть распознавала 8 объектов, представленных на рис. 4.

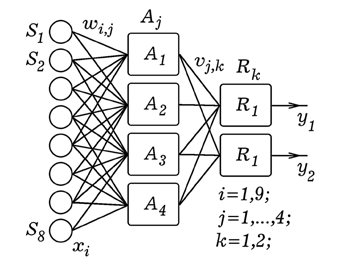
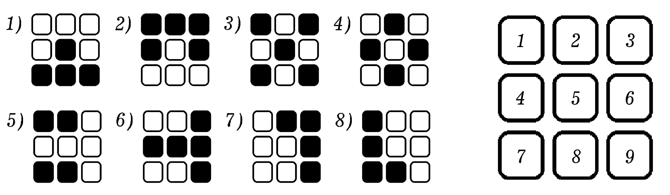
Рис. 4. Объекты для распознования.

Объекты закодируем так: o[1]={000010111}, o[2]={111101000} и т. д. Пусть им соответствуют следующие сигналы на выходах нейронов: y[1,j]={0000}, y[2,j]={1111}, y[3,j]={1001}, y[4,j]={0110}, y[5,j]={1010}, y[6,j]={0101}, y[7,j]={1100}, y[8,j]={0011}. Рис. 5. Схема нейросети.

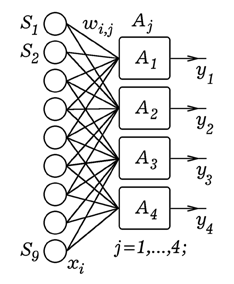
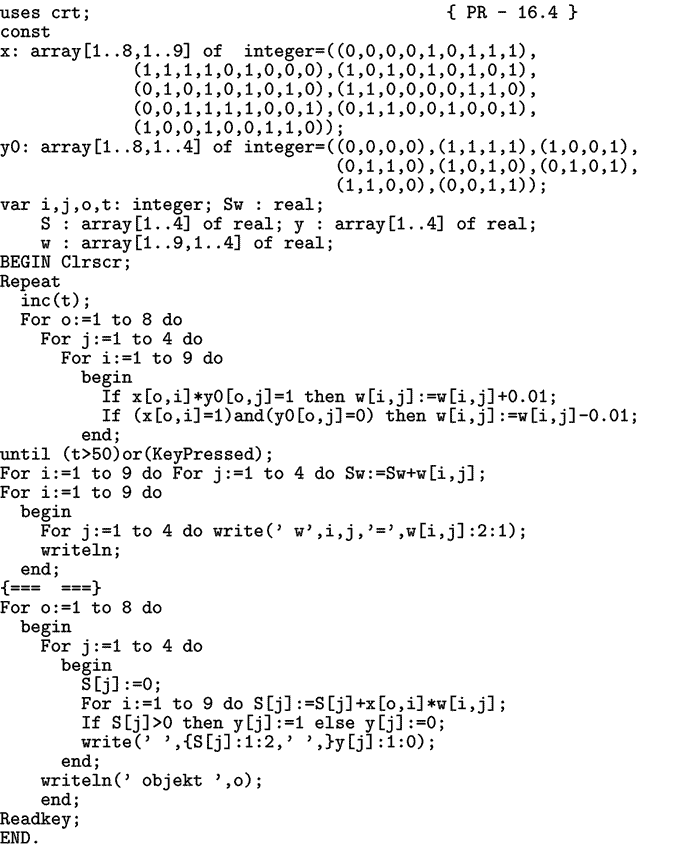
Необходимо последовательно предъявлять нейросети (рис. 5) объекты o[1], o[2],... , o[8] и изменять вес в соответствии с правилом: 1) если вход x[i] и выход y[j] одновременно возбуждены, то вес связи w[i,j] увеличивается; 2) если вход x[i] возбужден, а выход y[j] невозбужден, то вес связи w[i,j] уменьшается. Порог срабатывания для всех нейронов будем считать равным 0. Используется программа ПР-4. В результате расчетов получается матрица весов:

w[i,1]:=(1, 1, 1, -1, -0.5, 0, 0, -1, 0);

w[i,2]:=(-1, 1, 1, 1, -0.5, 2, -2, -1, 0);

w[i,3]:=(1, 1, -1, 1, -1.5, 0, 0, 1, -2);

w[i,4]:=(1, -1, 1, 1, 0.5, 0, 0, -1, 0).

Программа ПР-4.

Задача 5. Создайте компьютерную модель трехслойного персептрона, содержащего 3 ассоциативных и 2 реагирующих элемента. Подберите вес связей так, чтобы персептрон осуществлял классификацию объектов на 4 класса.

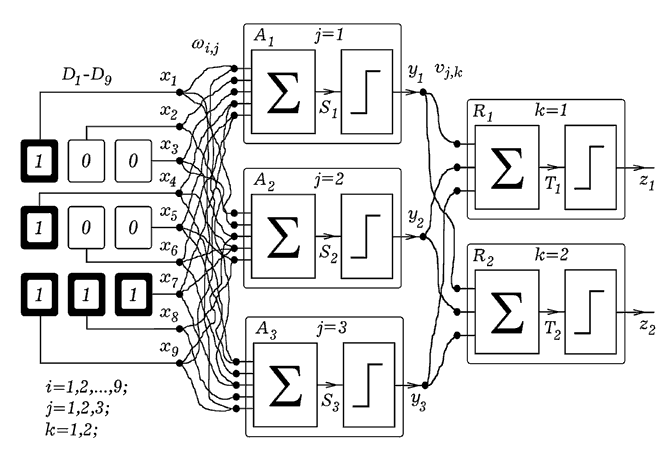
Рис. 6. Схема трехслойного персептрона.

Под персептроном понимают обучаемую нейросеть, состоящую из датчиков, ассоциативных и реагирующих элементов с заданной матрицей весовых коэффициентов. В многослойных персептронах присутствуют дополнительные слои ассоциативных элементов. В общем случае персептрон оперирует с цифровыми образами объектов, каждый из которых представим в виде массива нулей и единиц.

Рассмотрим трехслойный персептрон (рис. 6), состоящий из слоя сенсоров или датчиков D_i (i = 1, 2... 9), слоя ассоциативных элементов A_j (j = 1, 2, 3) и слоя реагирующих элементов R_k (k = 1, 2). Если уровень воздействия на датчик превышает некоторое пороговое значение h, то на его выходе появляется 1, а иначе - 0. Ассоциативный элемент работает как формальный нейрон: на выходе 1, когда сумма всего веса возбужденных входов превышает порог срабатывания; в противном случае на выходе 0. Вес входов w_i,j принимают значения -1, 0 или 1. Реагирующий R-элемент работает так: когда сумма всего веса возбужденных входов положительна, на выходе 1, а когда отрицательна - на выходе - 0. Вес входов v_j,k реагирующего элемента могут принимать произвольные значения. Выход реагирующего элемента имеет два состояния 0 и 1, поэтому персептрон с двумя решающими элементами может классифицировать объекты на четыре класса (2²=4), соответствующие выходным сигналам 00, 01, 10, 11.

Создать персептрон не просто, зато его можно сравнительно легко промоделировать на компьютере. Рассмотрим программу ПР-5, моделирующую работу трехслойного персептрона, изображенного на рис. 6. Допустим, персептрон должен различать четыре объекта, представленные ниже.

Учитывая расположение датчиков D_i (i = 1, 2, ..., 9), предъявляемые персептрону объекты кодируются так: O₁=(0,1,0,0,1,0,0,1,0), O₂=(0,0,0,1,1,1,0,0,0), O₃=(1,0,0,1,0,0,1,1,1), O₄=(1,1,1,0,0,1,0,0,1)). Чтобы персептрон правильно классифицировал объекты, необходимо задать вес связей, соединяющих датчики с ассоциативными элементами, и ассоциативные элементы с реагирующими элементами, следующим образом:

Порог срабатывания ассоциативных элементов h равен 0,5.

Программа ПР-5.

Результат работы программы представлен ниже. Из распечатки видно, какие значения принимают величины S_j, T_k, а также выходы y_j и z_k в случае, когда персептрону предъявляются объекты O₁, O₂, O₃, O₄. Объекту O₁ соответствуют состояния z₁=0, z₂=0, объекту O₂ - состояния z₁=1, z₂=0 и т. д. Таким образом, наша компьютерная модель персептрона распознает рассмотренные выше объекты. Вы можете дальше поэкспериментировать: изменить вес связей, предъявить персептрону другие объекты, промоделировать персептрон с тремя реагирующими элементами.

====== ОБЪЕКТ 1
j= 1 | S= -2.0 | y= 0.0
j= 2 | S= 0.0 | y= 0.0
j= 3 | S= -1.0 | y= 0.0
k= 1 | T= 0.0 | Выход z= 0
k= 2 | T= 0.0 | Выход z= 0
====== ОБЪЕКТ 2
j= 1 | S= 2.0 | y= 1.0
j= 2 | S= 0.0 | y= 0.0
j= 3 | S= -1.0 | y= 0.0
k= 1 | T= 2.0 | Выход z= 1
k= 2 | T= -2.0 | Выход z= 0
====== ОБЪЕКТ 3
j= 1 | S= -1.0 | y= 0.0
j= 2 | S= -3.0 | y= 0.0
j= 3 | S= 1.0 | y= 1.0
k= 1 | T= -2.0 | Выход z= 0
k= 2 | T= 2.0 | Выход z= 1
====== ОБЪЕКТ 4
j= 1 | S= 1.0 | y= 1.0
j= 2 | S= 3.0 | y= 1.0
j= 3 | S= 3.0 | y= 1.0
k= 1 | T= 2.0 | Выход z= 1
k= 2 | T= 2.0 | Выход z= 1

Тексты программ находятся в zip-архиве, файл gl-16.pas.

Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net .