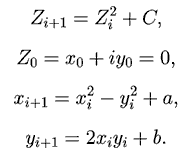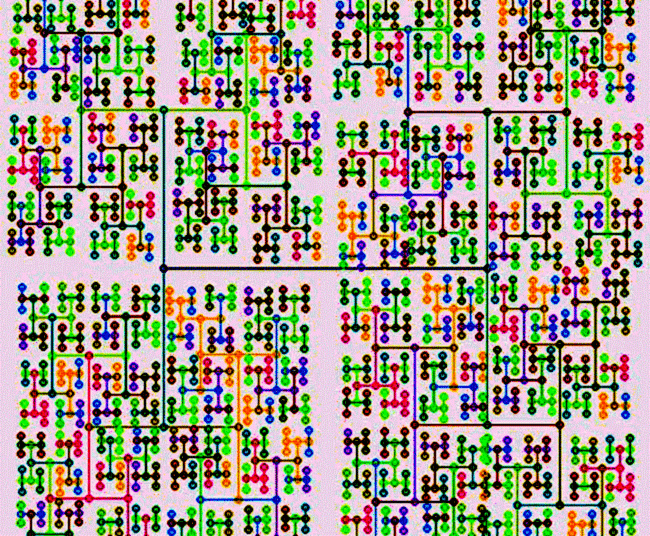МНОЖЕСТВО МАНДЕЛЬБРОТА И ДРУГИЕ ФРАКТАЛЫ
|
 |
Задача 1.
Напишите программу, которая строит известный фрактал --
множество Мандельброта.
|
Множество Мандельброта -- алгебраический фрактал, для построения которого
используется следующее правило. Берется точка комплексной плоскости
с координатами (a, b), соответствующая комплексному числу c = a + bi. К
этой точке n раз применяется преобразование:
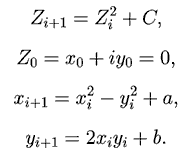
| 
|
Если в результате n преобразований точка удалится на 2 или более
единицы от начала координат, то она не принадлежит множеству Мандельброта,
она окрашивается в синий цвет. Если же расстояние от этой точки до начала
координат при любом числе итераций n (допустим n=200) останется меньше 2,
то точка принадлежит множеству Мандельброта и она окрашивается в красный
цвет. Программа ПР-1 для построения этого фрактала (рис. 1)
приведена ниже.
Для получения цветного изображения фрактала, точки, не принадлежащие
множеству Мандельброта, окрашиваются в цвет, зависящий от числа итераций,
после выполнения которых точка удаляется от начала координат на расстояние
больше чем 2.
Программа ПР-1.


Рис. 1. Множество Мандельброта.
 |
Задача 2.
Напишите программу, строящую простейший фрактал в виде дерева.
|
Программа должна строить горизонтальный отрезок [AB], от его концов
A и B рисовать два вертикальных отростка [AC] и [BD]. Затем снова
строить два горизонтальных отрезка меньшей длины [EF] и [GH], от
концов которых пойдут два вертикальных отрезка и т.д. Длины
горизонтальных отрезков на каждом шаге уменьшаются в a раз,
где a - случайное число в интервале от 1,5 до 3. Программа
ПР-2 представлена ниже, результат работы -- на рис. 2.
| 
|
Программа ПР-2.

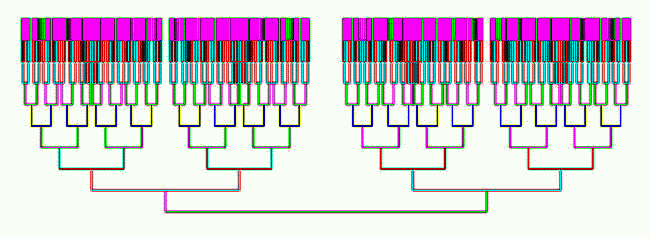
Рис. 2. Простейший фрактал.
 |
Задача 3.
Напишите программу, строящую фрактал, следующим образом: строится
горизонтальный отрезок [AB], затем пририсовываются два вертикальных
отрезка меньшей длины, чтобы их середины совпадали с концами A
и B. После этого строятся четыре горизонтальных отрезка меньшей
длины и т.д.
|
Используемая ПР-3 представлена ниже. С каждым следующим шагом
длины отрезков уменьшаются в a раз, где a - случайное число
из интервала [1,5; 1,9]. Поэтому получающийся фрактал называется
стохастическим. Процедура Draw рисует отрезки, а на концах строит
окружности (рис. 3).
| 
|
Программа ПР-3.

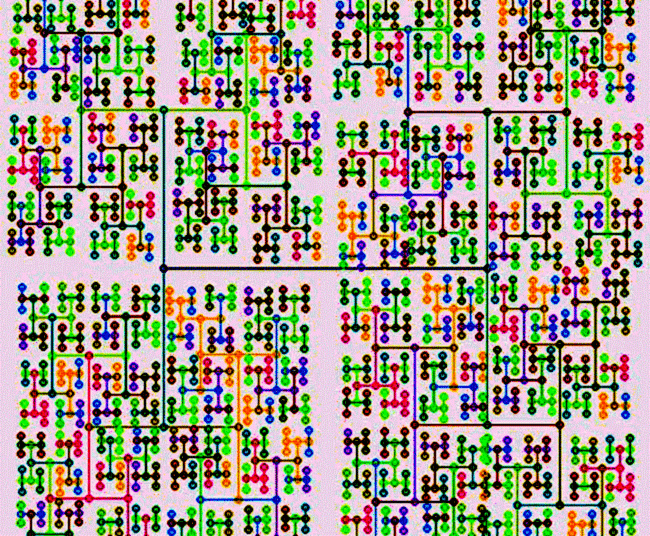
Рис. 3. Стохастический фрактал.
 |
Задача 4.
Постройте канторово множество: исходный отрезок разбейте на три части
и удалите середину. Затем повторите эту процедуру с получившимися двумя
отрезками, создав четыре отрезка. Выполнив эту операцию много раз,
получите фрактал.
|
Предлагаемая программа ПР-4 содержит рекурсивную процедуру, которая
делит отрезок на 3 части, отбрасывает среднюю часть и вызывает
саму себя для повторения этой операции с получившимися двумя
отрезками. Результат работы программы представлен на рис. 4.
| 
|
Программа ПР-4.

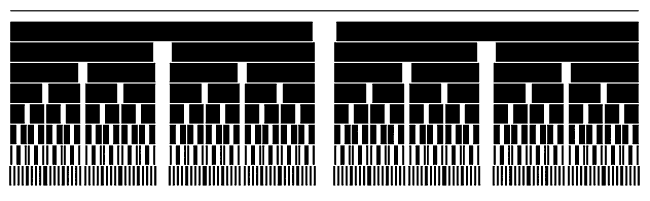
Рис. 4. Канторово множество.
 |
Задача 5.
Постройте фрактал по следующему алгоритму: программа выбирает в центре
экрана точку O и строит квадрат ABCD с длиной стороны L. После
этого она строит квадраты вокруг вершин A, B, C, D с длинами сторон
L/a и т.д., где a - случайная величина в интервале [2; 2,5].
|
Программа ПР-5 содержит рекурсивную процедуру, которая вызывает
сама себя. При каждом вызове счетчик n увеличивается на 1,
пересчитывается длина стороны L (уменьшается в a раз, где a -
случайная величина из интервала [2, 2.5]), изменяется цвет
рисуемых квадратов (рис. 5).
| 
|
Программа ПР-5.


Рис. 5. Фрактал из квадратов.
 |
Задача 6.
Постройте фрактал по следующему алгоритму. Плоская поверхность разбита
на клетки, находящиеся в состоянии 0. Если клетка перешла в возбужденное
состояние 1, то вероятность перехода соседних четырех клеток в состояние
1 на следующем шаге становится большой. Если невозбужденная клетка
граничит с двумя, тремя или четырьмя возбужденными клетками, то
вероятность ее перехода в состояние 1 уменьшается.
|
Пусть на плоской поверхности, разбитой на квадратные клетки,
находятся бактерии. Клетку, внутри которой они находятся,
будем считать возбужденной (a[i,j]=1). Бактерии могут переходить в смежную
клетку (например, [i+1,j]), которая при этом тоже станет возбужденной
(была a[i+1,j]=0, стала a[i+1,j]=1). Допустим, что бактерии из клетки
[i,j] живут за счет питательных веществ, находящихся в соседних четырех
клетках [i-1,j], [i+1,j], [i,j-1], [i,j+1]. Тогда вероятность
возбуждения клетки в состоянии 0 тем меньше, чем больше возбужденных
соседей она имеет. Можно также учесть и время, в течение которого
соседние клетки были возбуждены и жили, потребляя питательное вещество из
данной клетки.
Для моделирования этого процесса используется программа ПР-6.
В ней перебираются все клетки и вычисляется число возбужденных
соседей, результаты сохраняются в массиве b[i,j] (рис. 6).
| 
|
Программа ПР-6.

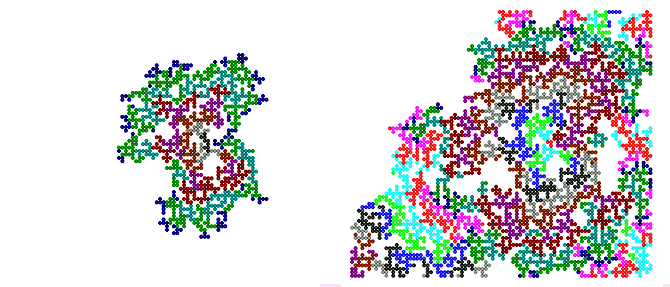
Рис. 6. Стохастический фрактал.
Тексты программ находятся в zip-архиве,
файл gl-17.pas.
ВВЕРХ
Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс].
- Глазов: ГГПИ, 2012 //
Web-site http://maier-rv.glazov.net .
|