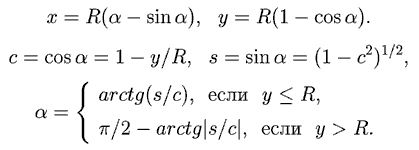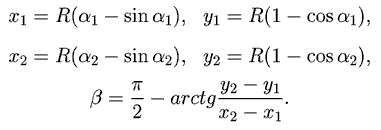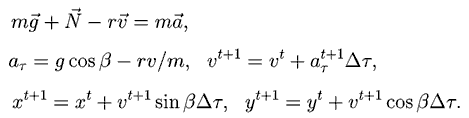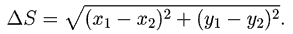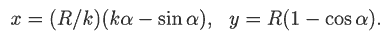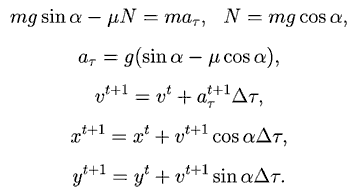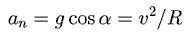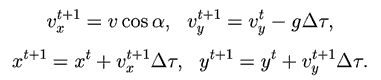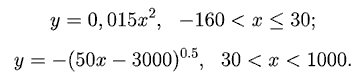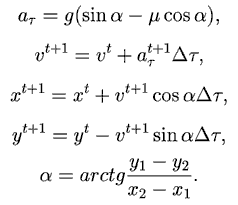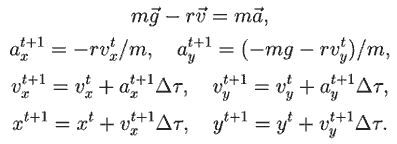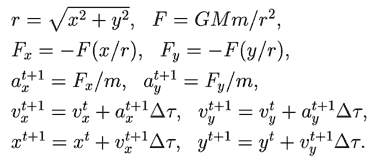|
Задача 2.1
Промоделируйте скольжение материальной точки по циклоидальной горке
в поле тяжести. Убедитесь в том, что циклоида является таутохроной,
то есть время скольжения к основанию горки не зависит от точки запуска.
|
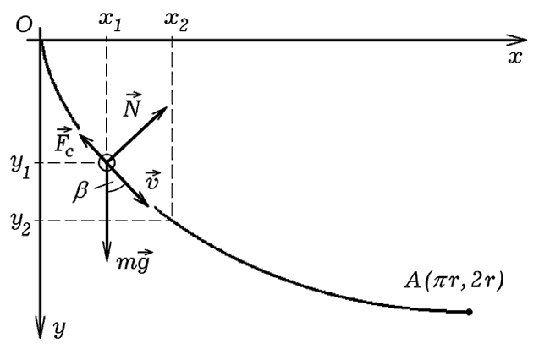
Рис. 2.1. К доказательству таутохронных свойств циклоиды.
Исследуем скольжение точки по циклоидальной горке и вычислим
время движения при различных начальных положениях точки (рис. 2.1).
Запишем уравнения циклоиды и выразим параметр α:
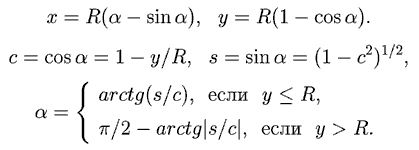
Чтобы определить угол β, найдем координаты двух близко
расположенных точек, соответствующих значениям параметра
α1, α2, и выразим
угол β между касательной к траектории и осью Oy равен:
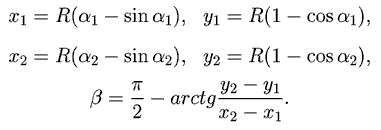
Для расчета тангенциального ускорения точки, скорости и
координат используются формулы:
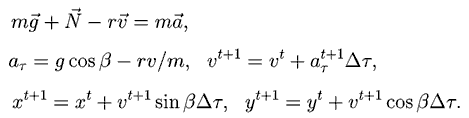
Таким образом, программа ПР - 2.1, моделирующая скольжение тела по
циклоидальной горке, должна содержать цикл по времени, в котором будут
пересчитываться координаты и скорости частицы, осуществляться построения
ее изображения на экране, вычисляться время движения, которое также
выводится на экран. Изменяя начальное значение α, можно запускать
точку с различных положений. При отсутствии трения (rs=0) время скольжения
не зависит от точки запуска (в пределах погрешности вычислений).
| 
|

 |
Задача 2.2
С помощью вычислительного эксперимента убедитесь в том,
что циклоида является брахистохроной - кривой наибыстрейшего
спуска.
|
Рассмотрим скольжение частицы массой m по циклоидальной горке
в однородном поле тяжести. Исходя из параметра α можно
вычислить координаты частицы x1 и y1. Если
параметру α дать малое приращение Δα и рассчитать
соответствующие координаты x2, y2, то
элементарное перемещение ΔS можно найти по формуле:
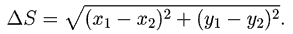
Скорость v вычисляется из закона сохранения механической энергии:
v=(2gy)1/2. Это позволяет определить промежуток времени
Δt=ΔS/v, в течение которого частица, двигаясь со
скоростью v, прошла расстояние ΔS. Суммируя элементарные
промежутки времени Δt, можно получить общее время
скольжения частицы по кривой из точки O(0,0) до точки A(πR, 2R).
Допустим, необходимо сравнить время скольжения частицы по циклоиде
с аналогичным временем движения по другой кривой, достаточно близкой к
циклоиде и проходящей через точки O(0,0) и A(πR, 2R). Эти кривые могут
быть заданы уравнениями:
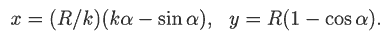
где k - некоторый параметр. Видно, что независимо от значения k при
кривые соединяют точки O(0,0) и A(πR, 2R). При k = 1 получается
циклоидальная траектория. В программе можно создать цикл, в котором
с некоторым шагом будет изменяться параметр k и вычисляться время
движения материальной точки по соответствующей кривой. При k = 1
время должно быть минимально. Текст используемой программы ПР - 2
приводится ниже. При ее запуске на экране рисуются траектории,
соответствующие различным значениям (рис. 2.2), рассчитывается
время движения частицы и выводится на экран. Из результатов
вычислительного эксперимента следует, что минимальным является время
движения по циклоиде (k = 1).
| 
|

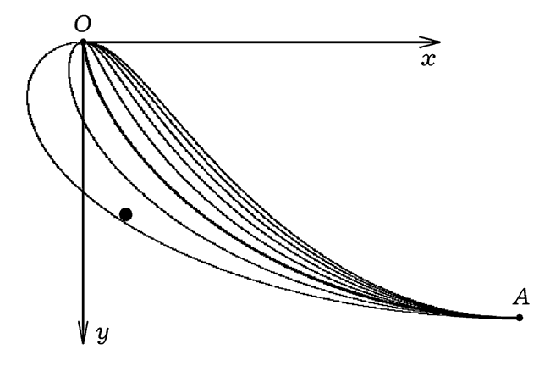
Рис. 2.2. К доказательству брахистохронных свойств циклоиды.
 |
Задача 2.3
Промоделируйте скольжение частицы по сферической поверхности и
ее движение после отрыва. Найдите точку отрыва.
|
Допустим, шайба скользит по шероховатой сферической поверхности и
отрывается от нее на некоторой высоте h. Необходимо рассчитать
траекторию шайбы и время движения. Из второго закона Ньютона
можно вычислить ускорение, скорость и координаты точки в последовательные
моменты времени:
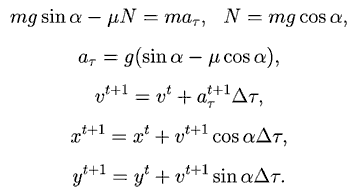
В момент отрыва шайба движется с ускорением g, при этом ее нормальное
ускорение равно:
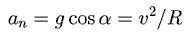
После отрыва от сферической поверхности шайба движется под
действием силы тяжести:
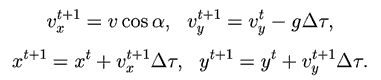
Используется программа ПР - 2.3, в ней
определяется высота h отрыва шайбы и общее время движения,
которое выводится на экран. Результат моделирования приведен
на рис. 2.3.
| 
|

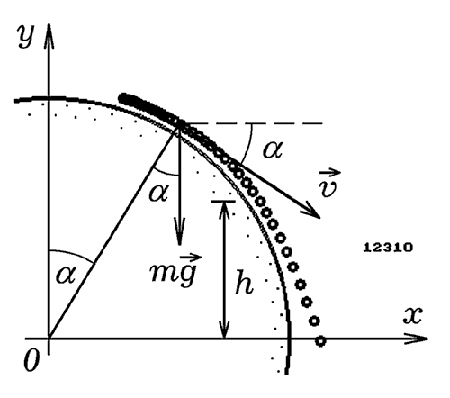
Рис. 2.3. Скольжение частицы по сферической поверхности.
 |
Задача 2.4.
Изучите движение лыжника, скатывающегося с горы и прыгающего с
трамплина на склон. Профили горки и склона заданы.
|
Пусть профиль горки и склона, на который прыгает лыжник, задаются
уравнениями:
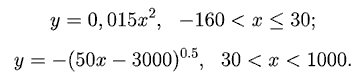
Для расчета движения лыжника используются уравнения:
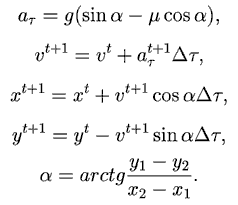
Программа ПР - 2.4 содержит цикл по времени, в котором пересчитываются
координаты и скорость лыжника в последовательные моменты времени,
а результаты выводятся на экран (рис. 2).
| 
|

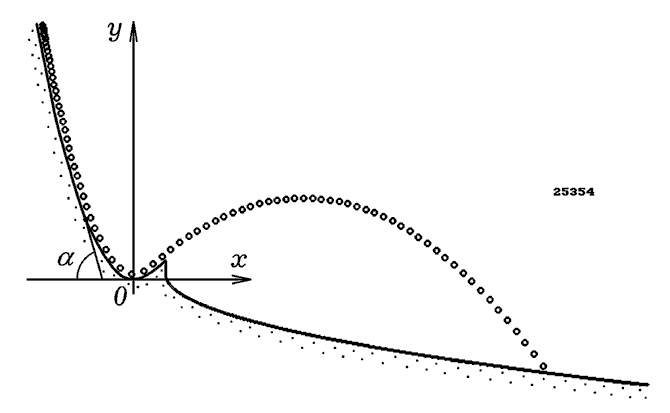
Рис. 2.4. Движение лыжника.
 |
Задача 2.5
Из пушки вылетает снаряд с известной скоростью. Определите
угол, под которым необходимо произвести выстрел, чтобы
снаряд попал в цель. Сила сопротивления, действующая на снаряд,
пропорциональна его скорости.
|
При движении снаряда на него со стороны воздуха действует сила
вязкого трения. Запишите второй закон Ньютона в конечных
разностях:
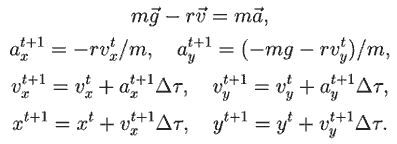
Для решения задачи используется метод стрельбы:
в программе ПР - 2.5 определяется
траектория движения снаряда при заданной начальной скорости и
произвольном угле α между стволом орудия и горизонталью.
Если снаряд не поразил цель, то угол α увеличивают на
некоторый шаг Δα и повторяют расчет, затем еще раз
и еще раз, до тех пор, пока снаряд не попадет в цель. Искомое
значение угла в радианах выводится на экран компьютера.
Задача имеет два решения. На рис. 2.5 показан метод нахождения
одного из них.
| 
|

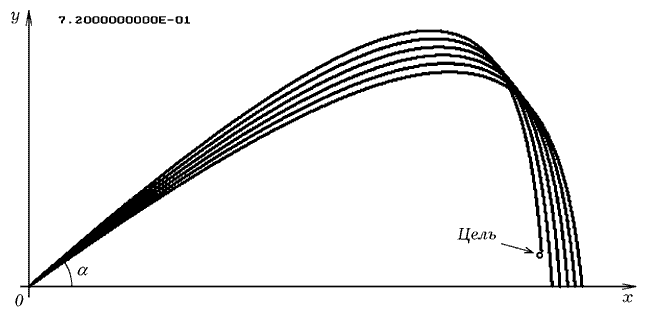
Рис. 2.5. Определение направления ствола
методом стрельбы.
 |
Задача 2.6
Ракета движется вокруг Земли по круговой орбите радиуса R. При однократном
включении двигателя в течение заданного интервала времени скорость
ракеты увеличивается в k раз. Промоделируйте переход спутника на
круговую орбиту с большим радиусом R.
|
Свяжем с центром Земли инерциальную систему отсчета. На спутник
действует сила гравитационного притяжения, проекции его ускорения,
скорости, а также его координаты в последовательные моменты времени
вычисляются по формулам:
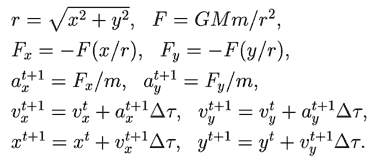
В программе ПР - 2.6 моделируется переход спутника с одной круговой
орбиты на другую более высокую орбиту. Для этого в моменты времени
t=20000 и t=40000 следует на небольшое время включить двигатели так,
чтобы скорость спутника возросла в k раз. Результат расчета траектории
движения спутника представлен на рис. 2.6.
| 
|
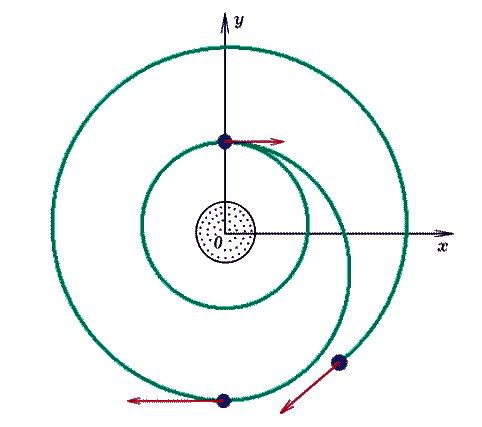
Рис. 2.6. Переход спутника на более
высокую орбиту.
Тексты программ находятся в zip-архиве,
файл gl-2.pas.
ВВЕРХ
Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс].
- Глазов: ГГПИ, 2012 //
Web-site http://maier-rv.glazov.net .
|