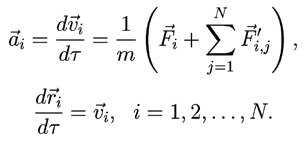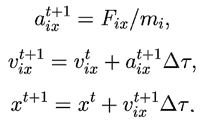|
ДВИЖЕНИЕ ЧАСТИЦ ЖИДКОСТИ И ГАЗА
|
 |
Задача 1.
Создайте двумерную модель газа, рассматривая молекулы как частицы,
между которыми действуют силы отталкивания.
|
Рассмотрите систему материальных точек, движущихся по плоскости,
на которые действуют внешние силы Fi (например, сила
тяжести) и внутренние силы F'i. Из второго закона
Ньютона следует:
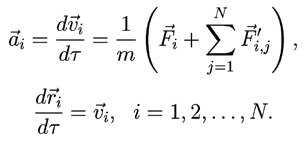
Программа, моделирующая движение молекул, должна содержать
цикл по времени t, а также цикл, в котором перебираются все
молекулы, вычисляются проекции действующих на них сил, определяются
ускорение, скорость и координата в следующий момент времени:
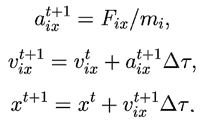
Используется программа ПР-1.
| 
|
Программа ПР-1.

 |
Задача 2.
Используя решение предыдущей задачи, создайте компьютерную модель
диффузии двух газов. Считайте молекулы газов твердыми шарами,
между которыми действуют силы отталкивания.
|
Для решения задачи следует промоделировать движение нескольких
десятков молекул двух сортов внутри прямоугольного сосуда.
Чтобы учесть отражение молекул от стенок в результате абсолютно
упругого удара, будем использовать операторы:
If (x[i]>500)or(x[i]<100) then vx[i]:=-vx[i];
If (y[i]>200)or(y[i]<100) then vy[i]:=-vy[i];
Результат работы программы ПР-2, моделирующей диффузию,
представлен на рис. 1.
| 
|
Программа ПР-2.

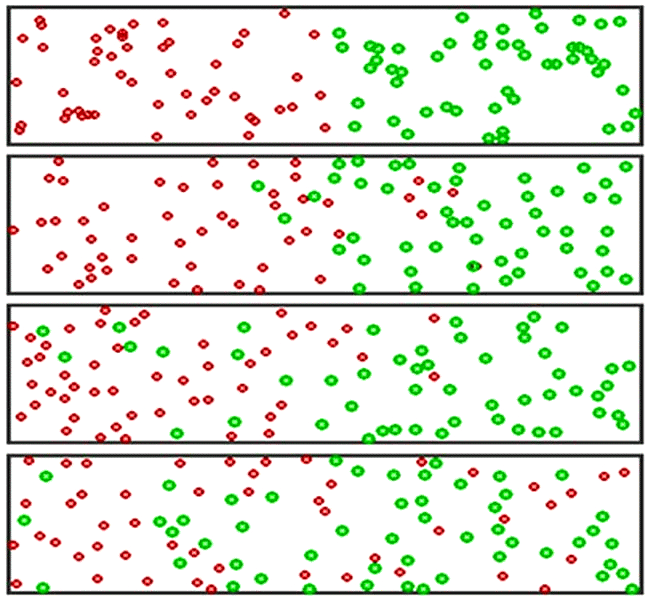
Рис. 1. Моделирование диффузии двух газов.
 |
Задача 3.
Рассматривая вязкую жидкость как совокупность твердых шарообразных
частиц, между которыми действуют силы притяжения и отталкивания,
промоделируйте падение жидкого цилиндра на выступ.
|
Будем моделировать жидкость как совокупность частиц (шариков),
между которыми действуют силы притяжения (при удалении) и
отталкивания (при сближении). Движение каждого шарика подчиняется
второму закону Ньютона и рассчитывается так, как в задаче 1.
На систему частиц действует сила тяжести, она, как единое
целое, падает на выступ или горизонтальную поверхность.
Используется программа ПР-3, результат моделирования
представлен на рис. 2.
| 
|
Программа ПР-3.

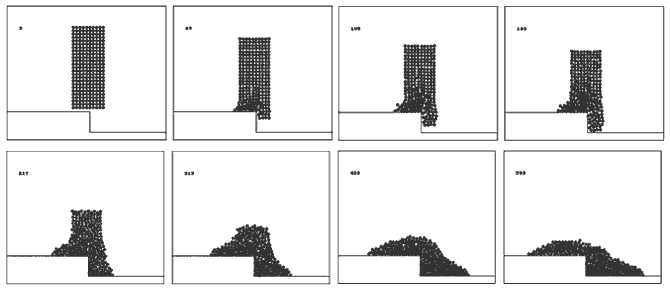
Рис. 2. Падение столба жидкости на выступ.
 |
Задача 4.
Промоделируйте обтекание пластины газом (сжимаемой жидкостью).
Газ следует представлять в виде совокупности частиц-маркеров,
между которыми действуют силы притяжения и отталкивания.
|
Рассмотрите двумерную модель газа, представляющую собой
совокупность частиц-маркеров, каждый из которых соответствует
элементарному объему. При удалении маркеров между ними действуют
силы притяжения, а при сближении - силы отталкивания. Пусть на
частицы-маркеры действует сила тяжести, в результате
чего они движутся вниз. Поставьте на пути их движения препятствие,
от которого частицы будут отталкиваться. Используемая программа
ПР-4 позволяет получить результаты, представленные на рис. 3.
| 
|
Программа ПР-4.

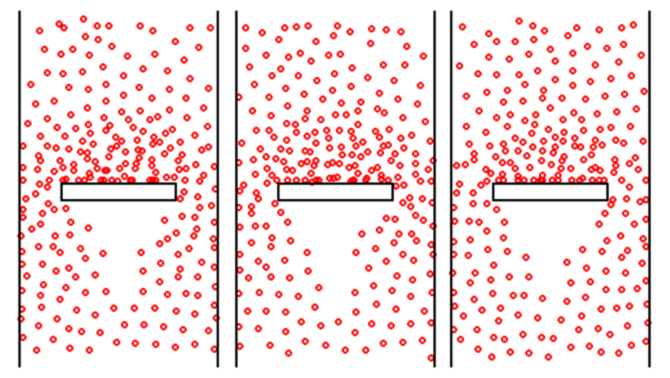
Рис. 3. Обтекание пластины газом (рисунки соответствуют
различным моментам времени).
 |
Задача 5.
Промоделируйте конвекцию газа в прямоугольном сосуде
с помощью частиц-маркеров, между которыми действуют
силы отталкивания.
|
Допустим, квадратный сосуд заполнен двумерным газом, который
моделируется совокупностью частиц-маркеров. Эти частицы
соответствуют элементарным объемам газа, они имеют равные массы,
координаты x[i] и y[i], скорости vx[i] и vy[i] и температуры t[i].
Между частицами-маркерами действуют силы отталкивания, вычисляемые
в процедуре Sila. Левая часть сосуда нагревается, температура
частиц с x[i]<50 равна t[i]:=1, на них действует сила, направленная вверх.
Правая часть сосуда охлаждается, температура частиц с x[i]>150
составляет t[i]:=-1, на них действует сила, направленная вниз.
| 
|
Чтобы промоделировать конвекцию газа, необходимо учесть,
что давление в точках, лежащих на одной горизонтали,
примерно одинаково. То есть молекулы (а значит и частицы-маркеры),
поднимающиеся вблизи левой стенки вверх, не должны скапливаться
в левом верхнем углу сосуда. Для учета этого фактора сосуд
разбивается на 16 квадратов. В процедуре Davlenie рассчитывается
число частиц-маркеров в каждом квадрате, считается, что оно
пропорционально давлению газа. Если в левом квадрате давление
меньше, чем в данном, то на частицы данного квадрата действует сила,
направленная влево. Если в правом квадрате давление
меньше, то на частицы действует сила, направленная вправо.
Это учитывается в процедуре Sila. Используется программа ПР-5.
На рис. 4 показаны траектории частиц-маркеров за небольшой промежуток
времени. Левый рисунок соответствует ситуации, когда частицы движутся
хаотично, конвекция отсутствует.
Программа ПР-5.

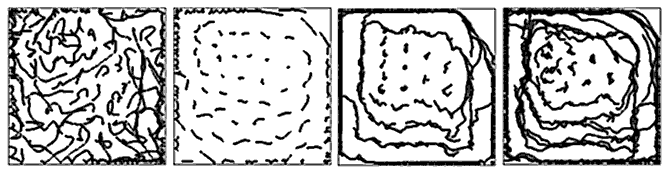
Рис. 4. Конвекция двумерного газа.
 |
Задача 6.
Рост некоторых природных объектов (кораллов, снежных хлопьев)
происходит в результате случайного присоединения частей.
Этот процесс называется агрегацией с ограничением диффузии.
Возникает фрактал, имеющий древовидную структуру и называющийся
дендритом. Напишите программу, моделирующую рост дендрита.
|
Промоделируйте хаотическое движение молекул некоторого вещества
в растворе. Все молекулы находятся в состоянии 0.
Когда какая-нибудь молекула достигнет ячейки с
затравочной частицей, она перейдет в состояние 1, остановится
и изменит свой цвет. Если другая частица приблизится
к молекуле, находящейся в состоянии 1, она как бы осядет,
присоединится к ней, тоже перейдя в состояние 1. Частицы,
находящиеся в состоянии 0, продолжают хаотически двигаться
и оседать на частицах, находящихся в состоянии 1.
В результате растет фрактал, имеющий древовидную структуру.
Частицы, обусловливающие его рост, не могут проникнуть в глубь
образующегося дендрита, они оседают на его периферии.
Используется программа ПР-6, результат ее работы
представлен на рис. 5. В ней используются периодические граничные
условия: когда частица выходит через левую границу квадратной ячейки,
она входит в нее через правую границу; когда частица выходит через
нижнюю границу квадратной ячейки, она входит в нее через верхнюю
границу и т. д.
| 
|
Программа ПР-6.


Рис. 5. Рост дендрита.

Рис. 6. Дендрит имеет фрактальную структуру.
Тексты программ находятся в zip-архиве,
файл gl-31.pas.
ВВЕРХ
Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс].
- Глазов: ГГПИ, 2012 //
Web-site http://maier-rv.glazov.net .
|