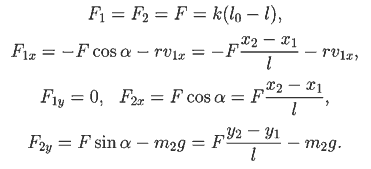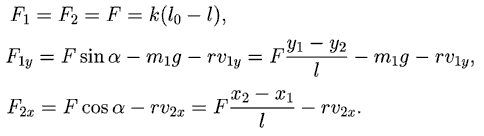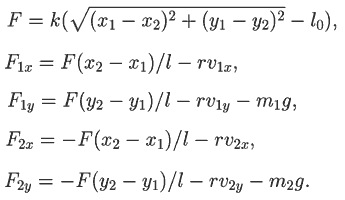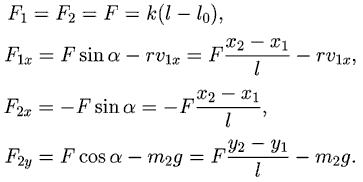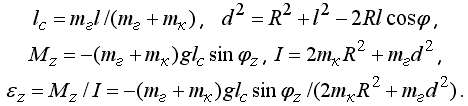|
Задача 1.
Стержень устанавливают на горизонтальную поверхность так, чтобы
он образовывал некоторый угол с вертикалью, и отпускают. Необходимо
рассчитать координаты его концов при падении в последовательные
моменты времени.
|
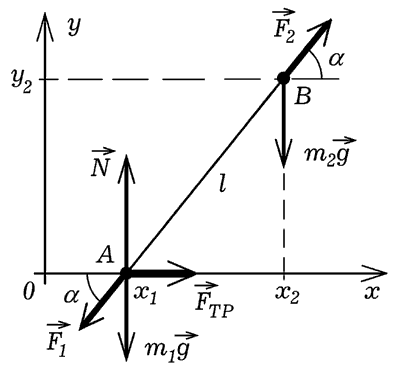
Рис. 1. Падение стержня на горизонтальную поверхность.
Рассмотрим систему, состоящую из двух материальных
точек m1 и m2, связанных между собой
невесомым упругим стержнем (рис. 1). Длина стержня в недеформированном
состоянии равна l0, при его сжатии возникают силы
упругости F1 и F2. Будем считать, что нижний
конец стержня A скользит по горизонтальной поверхности, не
отрываясь от нее (y1=0). При этом на него действует
сила вязкого трения FТР, пропорциональная скорости и
направленная в сторону, противоположную движению. Проекции сил,
действующих на материальные точки m1 и m2,
вычисляются из формул:
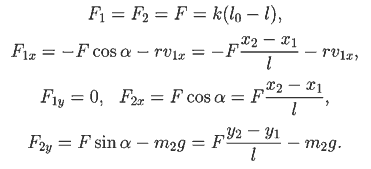
| 
|
В программе ПР-1 в последовательные моменты времени пересчитывают
силы, действующие на материальные точки, их ускорения, скорости
и координаты. Результаты моделирования падения стержня при
различных значениях коэффициента сопротивления r представлены на
рис. 2. При необходимости можно рассчитать траекторию движения
центра масс стержня, зависимость его угла наклона от времени и т. д.
Программа ПР-1.

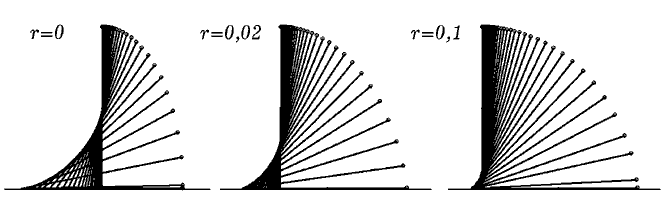
Рис. 2. Результаты моделирования падения стержня.
 |
Задача 2.
Лестницу прислоняют к стене и отпускают. Напишите программу,
моделирующую падение лестницы, если известно, что ее
концы с трением скользят по поверхностям стены и пола,
не отрываясь от них.
|
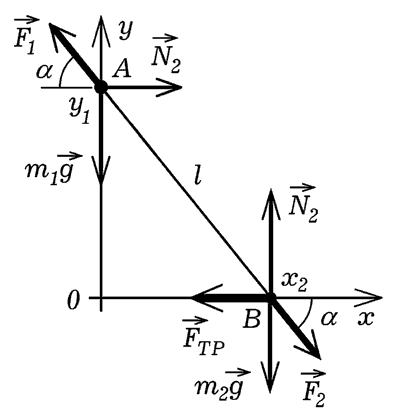
Рис. 3. Падение стержня на горизонтальную поверхность.
Вместо лестницы рассмотрим систему двух материальных точек
массами m1 и m2, соединенных невесомым
упругим стержнем жесткостью k и длиной l0. Эти
точки как бы скользят по вертикальной и горизонтальной
направляющим, при этом на них действует сила вязкого трения,
прямо пропорциональная скорости и направленная в противоположную
сторону (рис. 3). Найдем действующие на точки силы:
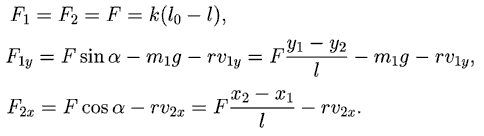
| 
|
Программа ПР-2 содержит цикл по времени, в котором вычисляются
силы, действующие на материальные точки, определяются их ускорения,
скорости и координаты, а также координаты центра масс. На экране
монитора изображается положение лестницы в последовательные моменты
времени (рис. 4).
Программа ПР-2.
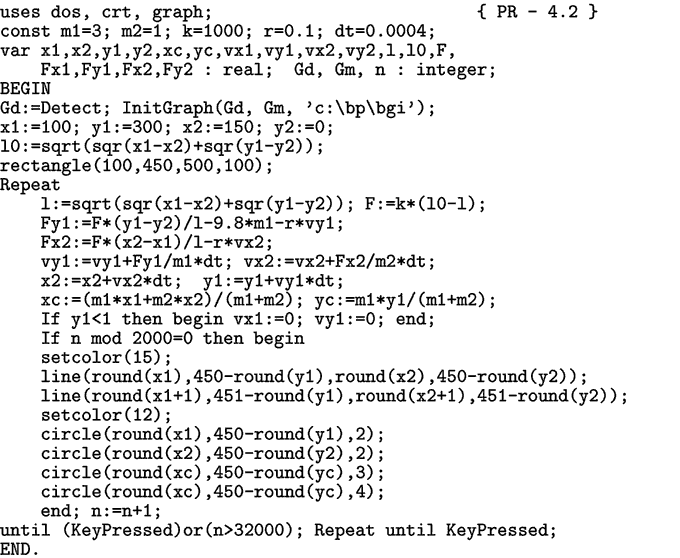
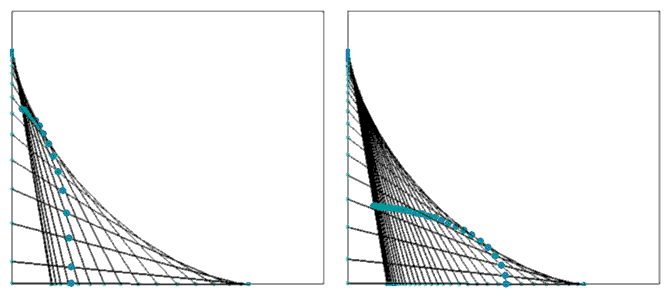
Рис. 4. Падение стержня на горизонтальную поверхность.
 |
Задача 3.
Промоделируйте плоское движение тела в поле тяжести, при котором
его центр масс движется по кривой, а само тело вращается вокруг
центра масс. Используйте модель, состоящую из двух материальных
точек, связанных упругим стержнем.
|
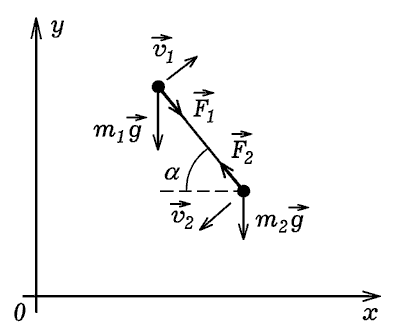
Рис. 5. Движение двух материальных точек, соединенных стержнем.
Рассмотрите систему из двух материальных точек, соединенных упругим
стержнем. Проекции сил, действующих на точки, могут быть вычислены
по формулам (рис. 5):
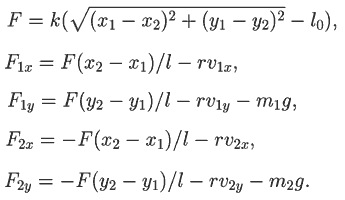
| 
|
Программа ПР-3 содержит цикл по времени, в котором вычисляются
действующие силы, ускорения, скорости и координаты точек. На экране
строятся положения стержня в последовательные моменты времени.
Программа позволяет промоделировать: 1) движение в поле тяжести и отскок
стержня от стены и пола (рис. 6); 2) движение системы в случае, когда
массы точек сильно отличаются; 3) движение системы при не очень большой
жесткости стержня.
Программа ПР-3.


Рис. 6. Движение палки в поле тяжести.
 |
Задача 4.
На тележке массой m1 подвешен маятник, состоящий из
тела массой m2 и нити длиной l. Маятник выводят из
положения равновесия и отпускают. В подшипниках тележки действует
сила вязкого трения. Напишите программу, моделирующую затухающие
колебания системы.
|
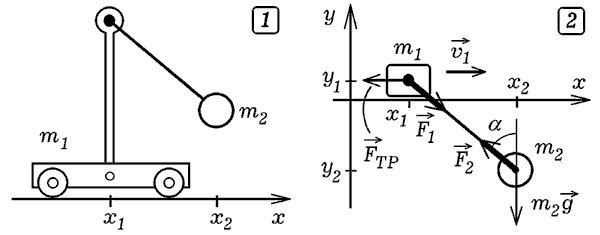
Рис. 7. Движение тележки с маятником.
Заменим систему "маятник-тележка" системой, состоящей из
двух материальных точек m1 и m2,
связанных упругим стержнем жесткостью k и длиной l0 (рис. 7).
Материальная точка m1 способна скользить по горизонтальной
линии так, что ее координата y2 остается постоянной.
При этом на нее действует сила вязкого трения, направленная
противоположно скорости и пропорциональная ее величине.
Проекции сил, действующих на точки системы, вычисляются по
формулам:
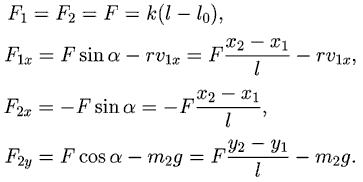
| 
|
В предлагаемой программе ПР-4 осуществляется расчет действующих на
точки сил, а также проекций их ускорений, скоростей и координат в
последовательные моменты времени. Результаты моделирования
представлены на рис. 8.
Программа ПР-4.

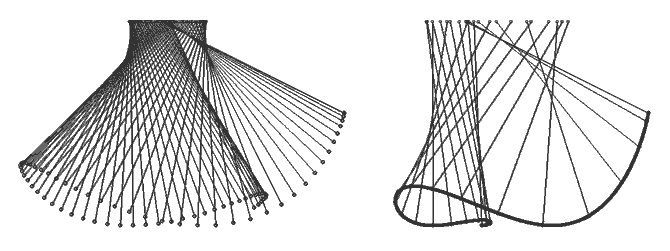
Рис. 8. Колебания маятника на тележке.
 |
Задача 5.
На горизонтальной поверхности покоится кольцо (труба), к внутренней стороне
которого прикреплен груз. Расстояние от оси кольца до его центра
масс известно. Кольцо смещают из положения равновесия и отпускают.
Изучите: 1) колебания кольца относительно положения равновесия;
2) движение кольца после того, как ему сообщили начальную скорость.
|
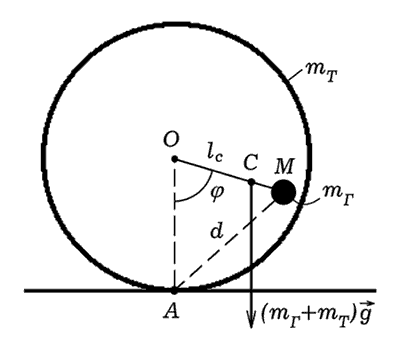
Рис. 9. Колебания кольца со смещенным центром тяжести.
Рассмотрим качение кольца по горизонтальной поверхности (рис. 9).
Необходимо рассчитать расстояние от центра кольца O до центра
масс C, момент M силы тяжести, момент инерции I относительно
мгновенной оси вращения A. Для этого следует использовать формулы:
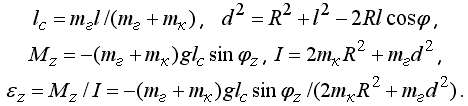
| 
|
Зная момент силы и момент инерции, можно определить угловое ускорение
тела в последовательные моменты времени, вычислить угловую скорость
и угол поворота, а также горизонтальную координату центра кольца. При
этом используется программа ПР-5, результаты представлены на
рис. 10 и 11. Чтобы промоделировать качение кольца со
смещенным центром масс, следует задать начальную скорость (рис. 12).
Программа ПР-5.

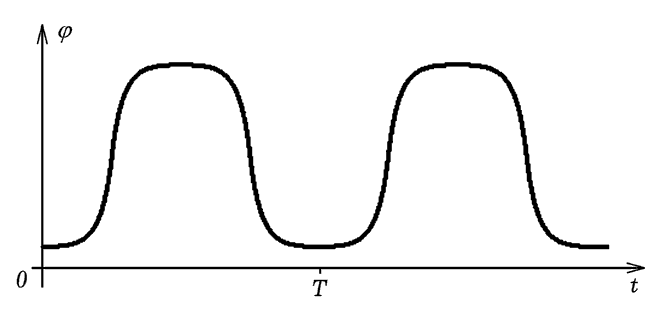
Рис. 10. Зависимость угла поворота от времени.
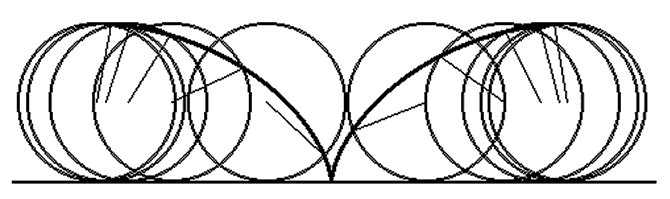
Рис. 11. Колебания кольца на горизонтальной поверхности.
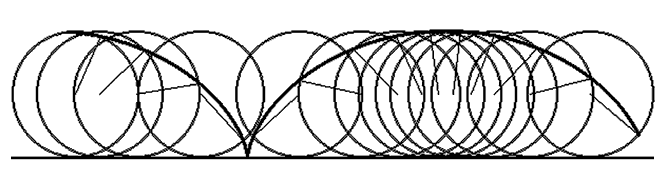
Рис. 12. Качение кольца со смещенным центром масс.
 |
Задача 6.
Брусок в форме прямоугольного параллелепипеда плавает на поверхности
жидкости. Координаты центра масс, плотности жидкости и бруска известны.
Определите расположение бруска относительно поверхности жидкости.
|
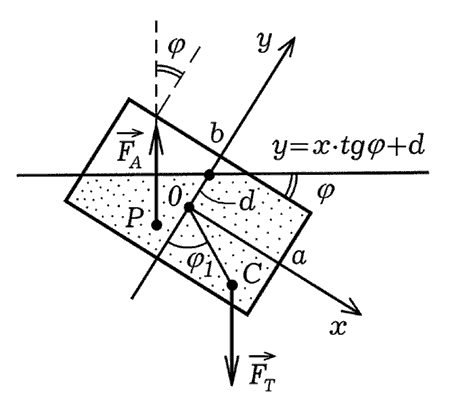
Рис. 13. К расчету положения тела.
Расположение бруска относительно поверхности воды однозначно
определяется величинами d и φ (рис. 13). Пусть a = 3, b = 1.
Задача решается так. Положим, что φ=0. Будем увеличивать d
от -3 с некоторым шагом, каждый раз вычисляя объем погруженной
части бруска и определяя силу Архимеда. Плотность бруска ρ
меньше плотности жидкости ρ0, поэтому сила Архимеда
превысит силу тяжести, когда тело не полностью погрузится в жидкость.
Нарисуем поверхность жидкости AB и определим положение центра
плавучести P.
Брусок будет находиться в положении устойчивого равновесия
тогда, когда центр масс C находится точно под центром плавучести P,
то есть углы φ и φ1 равны. Если это условие не
выполняется, будем увеличивать угол φ с некоторым шагом, каждый раз
определяя величину d, положение центра плавучести P и проверяя
равенство углов φ и φ1 (оно может выполняться
с небольшой погрешностью). Когда углы φ и φ1
окажутся равными, программы должна вывести результат вычислений.
| 
|
Для нахождения объема погруженной части тела Vp необходимо найти
площадь S фигуры, выделенной точками. Для этого используется метод
прямоугольников:

Чтобы найти координаты xpl и ypl центра плавучести, внутрь
прямоугольника случайным образом бросим 100000 точек и подсчитаем
количество точек, попавших в заштрихованную область S, соответствующую
погруженной части тела. Используется следующий фрагмент
программы:

Результаты работы программы ПР-6 представлены на рис. 14 и 15.
Программа рисует прямоугольное сечение бруска и определяет
положение поверхности жидкости AB и центра плавучести. Сила
Архимеда направлена вдоль вертикали MN. В состоянии устойчивого
равновесия центр масс C и центр плавучести P лежат на одной
вертикали MN. Изображение, получающееся на экране монитора,
представлено в левой части рис. 14 и 15.
Программа ПР-6.

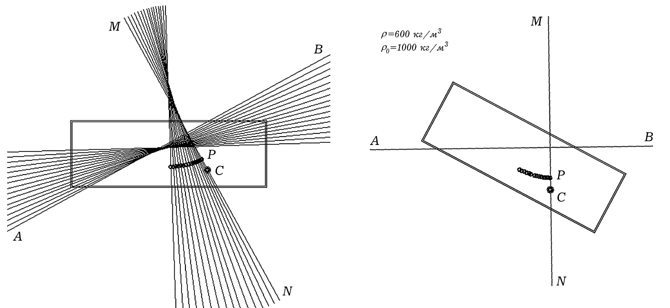
Рис. 14. Устойчивое состояние плавающего тела.
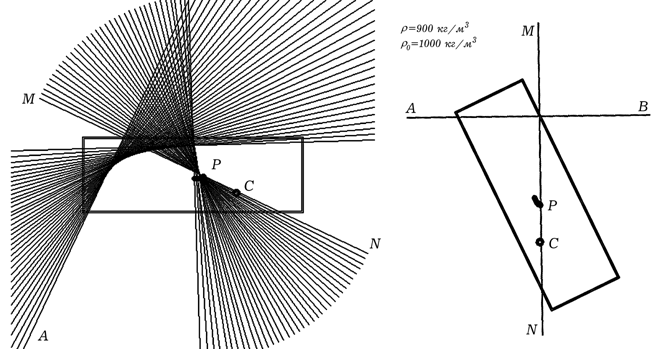
Рис. 15. Устойчивое состояние плавающего тела.
 |
Задача 7.
Вращающийся цилиндр (или колесо) двигаясь в однородном поле тяжести
под некоторым углом падает на горизонтальную поверхность с уступом.
Со стороны поверхности на него действуют сила упругости и сила вязкого
трения. Необходимо промоделировать движение цилиндра с течением времени.
|
Цилиндр мысленно заменим системой из девяти частиц, одна из которых расположена
в центре окружности радиуса R, а остальные восемь лежат на этой окружности и
делят ее на весемь равных дуг. Будем считать, что частицы соединены между собой
шестнадцатью невесомыми упругими стержнями: из них восемь радиальных стержней и
восемь стержней, соединяющих соседние частицы, лежащие на окружности. Расстояния
между i-той и j-той частицами, когда цилиндр недеформирован, записаны в массив
L[i,j] (программа ПР-7).
| 
|
В процедуре Sila перебираются все 9 материальных точек и рассчитываются
проекции сил, действующие на каждую точку. Для этого пересчитываются реальные
расстояния между частицами и определяются действующие на них силы упругости (их
проекции Fx[i] и Fy[i]). При соударении частицы с горизонтальной поверхностью
рассчитываются силы F1 и F2, складывающиеся из силы вязкого трения и силы
упругости. После этого пересчитываются скорости и координаты частиц в
следующий дискретный момент времени t+1.
Программа ПР-7.

Результаты моделирования представлены на рис. 16. Начальные условия заданы так,
чтобы подлетающий цилиндр до удара о поверхность вращался бы против часовой стрелки,
а после нескольких ударов -- по часовой стрелке.
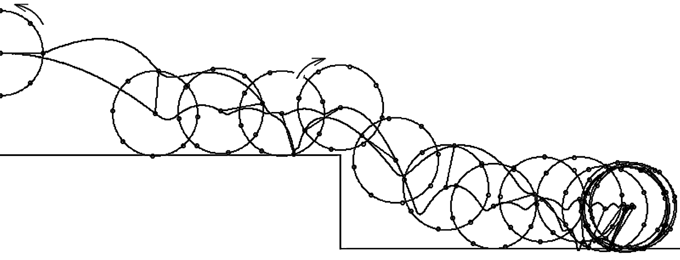
Рис. 16. Вращающийся цилиндр соударяется с поверхностью.
Тексты программ находятся в zip-архиве,
файл gl-4.pas.
ВВЕРХ
Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс].
- Глазов: ГГПИ, 2012 //
Web-site http://maier-rv.glazov.net .
|