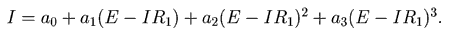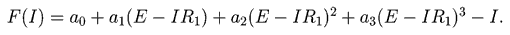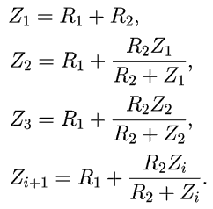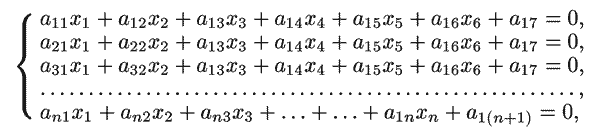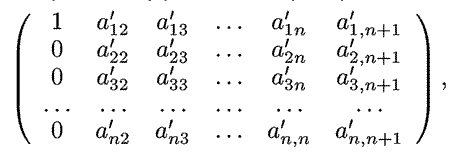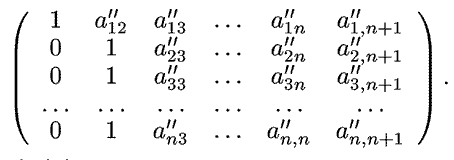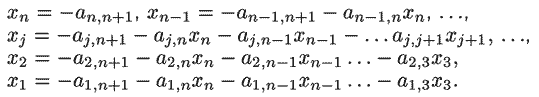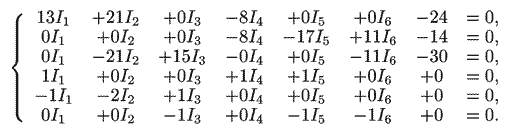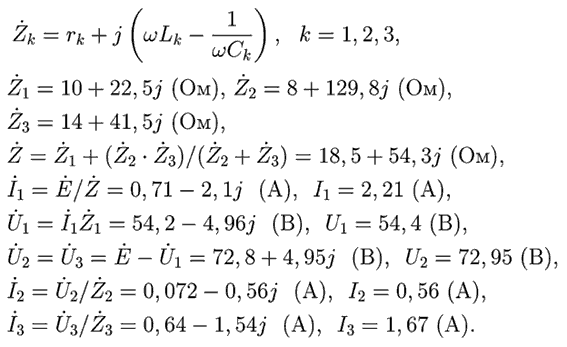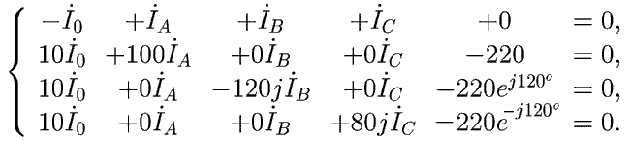РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
|
 |
Задача 1.
Электрическая цепь (рис. 1) состоит из источника постоянной
ЭДС E=200 В, резистора R1=400 Ом и нелинейного элемента,
вольт-амперная характеристика которого может быть аппроксимирована
многочленом третьей степени
i(u)=2+5u-0,18u2+0,002u3.
Рассчитайте ток в цепи.
|
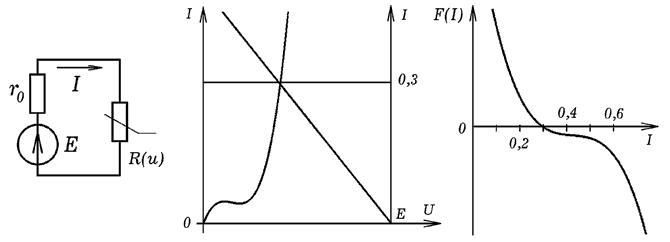
Рис. 1. Расчет нелинейной цепи
Вольт-амперные характеристики обоих элементов изображены на рис. 1
(ВАХ резистора повернута вокруг оси ординат и смещена на E).
Напряжение на нелинейном элементе равно U=E-IR1, поэтому для
нахождения искомого тока I следует решить нелинейное алгебраическое
уравнение:
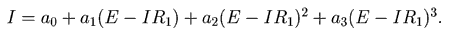
Чтобы решить уравнение, необходимо определить количество корней и
локализовать их, то есть установить интервалы, внутри которых находится
каждый корень. Воспользуемся графическим методом, для этого построим
график функции:
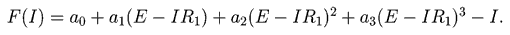
,
найдем точку его пересечения с осью абсцисс, для которой F(I)=0.
Она лежит в интервале 0,2 - 0,4 мА. Самым простым способом решения
подобных уравнений является табулирование функции F(I). Это может быть
реализовано с помощью алгоритма A - 1 (программа ПР-1). При запуске
программы на экран выводятся те значения тока, для которых функция
F(I) по модулю меньше чем ε =0,01, т. е. близка к нулю.
Это позволяет уменьшить неопределенность в нахождении корня до 0,01,
корень уравнения лежит в интервале от 2,960 до 2,965. Ответ:
ток примерно равен 2,962 А.
| 
|
Программа ПР-1.

Другой способ решения уравнения F(x)=0 состоит в использовании
метода половинного деления. Задается интервал
[a0, b0], содержащий
корень. График функции y=F(x) должен пересекать ось абсцисс внутри
интервала, на его границах функция имеет противоположные знаки, в чем
можно убедиться, проверив условие F(a0)F(b0)<0.
Отрезок [a0, b0] делится точкой с=(a+b)/2
пополам. Если F(c) = 0, то значение x = c и есть корень уравнения.
В противном случае из двух отрезков [a0,c] и
[c,b0] выбирается тот, внутри которого
график y = F(x) пересекает ось абсцисс. Для этого снова проверяется
условие F(c)F(b0)<0, если оно выполняется, то
a1=c, b1=b0. После этого
осуществляется следующая итерация: отрезок [a1, b1]
снова делится пополам и т.д. Так продолжается до тех пор, пока
длина отрезка [ai, bi] не окажется меньше
заданной точности ε.
Используется программа ПР-2.
Понятно, что ток в цепи не может превышать значение E/R1,
поэтому в качестве нулевого приближения к корню выберем интервал
[0, E/R1]. В результате последовательности итераций
при ε=0,0000001 получается корень уравнения 2,96296. Округляя
до четырех значащих цифр, получаем: ток равен 2,963 А.
Программа ПР-2.

 |
Задача 2.
Напишите программу, рассчитывающую сопротивление цепи,
состоящей из бесконечной цепочки резисторов R1=80 Ом
и R2=100 Ом (рис. 2).
|
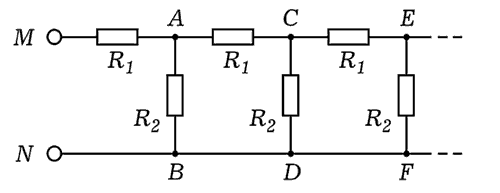
Рис. 2. Схема из бесконечной цепочки резисторов
Найдем сопротивление участка цепи MABN из двух ветвей,
участка цепи MACDBN из четырех ветвей, участка цепи
MACEFDBN из шести ветвей. Обобщим получающуюся формулу:
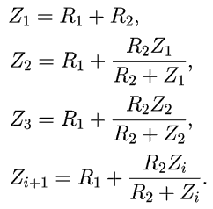
Программа ПР-3 последовательно вычисляет сопротивление
Z1, Z2, Z3, ... и
результат выводит на экран. Получающиеся значения стремятся
к величине 138 Ом.
| 
|
Программа ПР-3.

 |
Задача 3.
Напишите программу, решающую систему из N линейных
алгебраических уравнений.
|
Рассмотрим алгоритм, позволяющий решать систему из n линейных
алгебраических уравнений с n неизвестными, имеющую следующий вид:
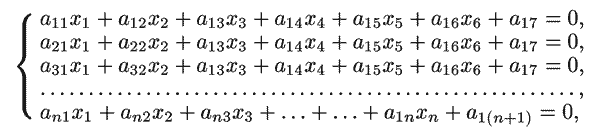
От этой системы перейдите к матрице из элементов
ai,j, где i=1, 2, ... , n и j=1, 2, ... , n+1.

Приведите данную матрицу к треугольному виду. Чтобы исключить деление
на ноль, сложите левые и правые части первого и второго, первого и третьего,
второго и четвертого уравнений и т. д. Первый шаг состоит в следующем:
разделите все элементы каждой строки матрицы (или каждого уравнения системы)
на первый коэффициент ai1, где i = 1, 2... n. Тогда
все элементы ai1 из первого столбца будут равны 1. Вычтите из
второго, третьего и последующих уравнений первое. Матрица коэффициентов
приобретет вид:
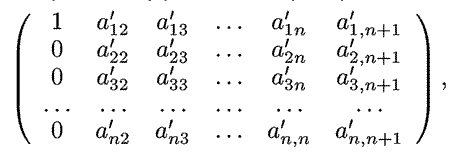
где a'i,j=ai,j/ai1-
a1j/a11, где i=1, 2, ... , n и
j = 1, 2... n + 1. После этого сделаем второй шаг: разделим
вторую, третью и последующие строки матрица на соответствующие
коэффициенты ai2, после чего вычтем из третьей,
четвертой и последующих строк вторую строку. Получим:
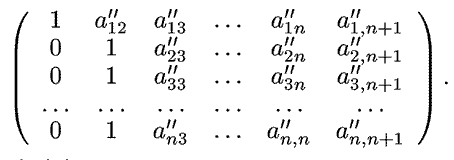
где a''ij=a'ij/a'i1-
a'1j/a'11, где i = 1, 2... n и
j = 1, 2... n + 1. После n-го шага получим матрицу
треугольного вида:
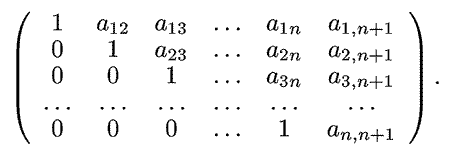
Искомые значения находятся по формулам:
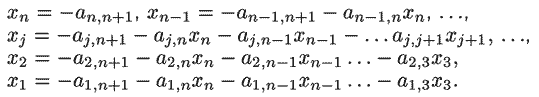
Желательно, чтобы программа осуществляла проверку решения, подставляя
найденные значения x1, x2... в исходную
систему уравнений. Текст такой программы ПР-4 представлен ниже.
| 
|
Программа ПР-4.

 |
Задача 4.
Рассчитайте цепь постоянного тока, состоящую из нескольких
контуров (рис. 3). Сопротивления резисторов
R1=13 Ом, R2=21 Ом, R3=15 Ом,
R4=8 Ом, R5=17 Ом, R6=11 Ом.
ЭДС источников E1=5 В, E2=13 В, E3=9 В,
E4=-6 В, E5=12 В, E6=-8 В.
|
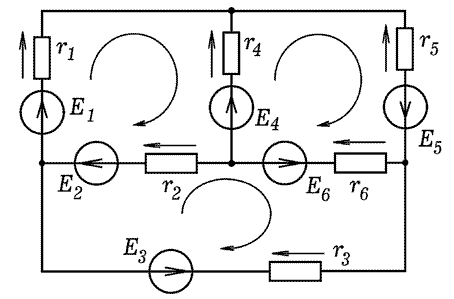
Рис. 3. Электрическая цепь постоянного тока
Используя законы Кирхгофа составьте систему уравнений.
Подставьте вместо сопротивлений и ЭДС конкретные значения,
перенесите все члены в левую часть:
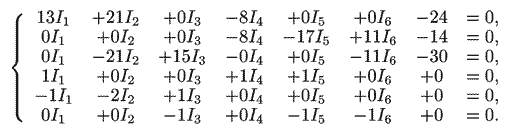
Для решения системы уравнений с n неизвестными используется программа
ПР-4. На экран выводятся значения переменных и осуществляется
проверка: в исходную систему подставляются найденные значения xi,
i = 1, 2... n. При этом левые части уравнений обращаются в ноль,
что подтверждает правильность решения. Итак, полученные значения
токов: I1=0,481 А, I2=0,812 А, I3=-0,331 А,
I4=-0,086 А, I5=-0,395 А, I6=0,726 А.
Знак минус означает, что реальное направление тока в соответствующей
ветви противоположно предполагаемому.
| 
|
 |
Задача 5.
Цепь состоит из источника переменной ЭДС и трех ветвей,
в каждой из которых резистор, конденсатор и катушка индуктивности.
Вторая и третья ветви соединены параллельно между собой, последовательно
с ними включена первая ветвь (рис. 4). Рассчитайте все токи и напряжения,
полную, активную и реактивную мощности. Постройте векторную диаграмму.
Определите действующие значения всех токов и напряжений.
|
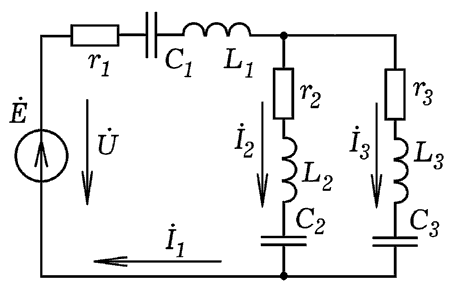
Рис. 4. Однофазная цепь переменного тока
Допустим, цепь имеет параметры:
R1=10 Ом, L1=0.08 Гн, C1=1200 мкФ,
R2=8 Ом, L2=0.42 Гн, C2=1500 мкФ,
R3=14 Ом, L3=0.14 Гн, C3=1270 мкФ.
Для вычисления импедансов, токов и напряжений для каждой ветви
используются формулы:
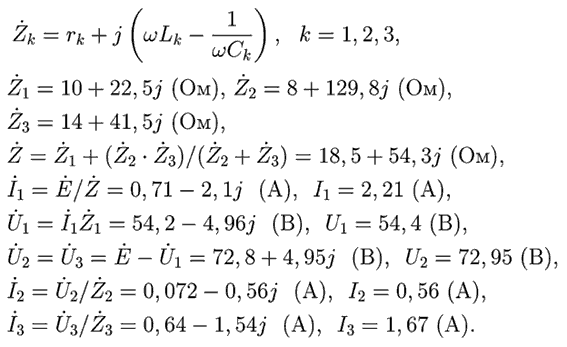
Представленная ниже программа ПР-5 содержит процедуры Sum, Razn,
Proizv, Delen, Modul, позволяющие определять сумму, разность,
произведение, отношение двух комплексных чисел и находить
модуль комплексного числа. С помощью этих процедур осуществляются
расчеты комплексов тока и напряжения, комплекса мощности.
| 
|
Программа ПР-5.
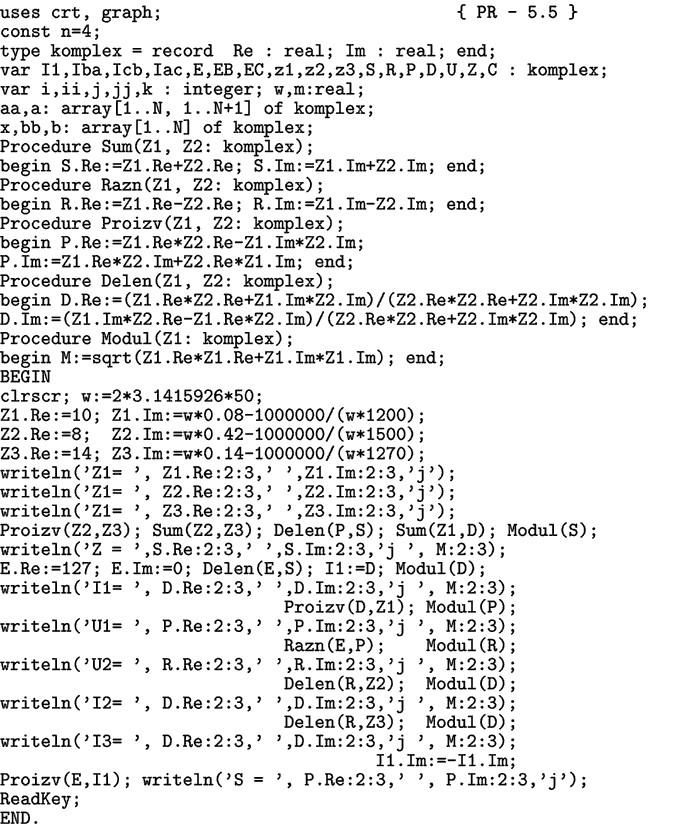
 |
Задача 6.
Напишите программу, решающую систему из N линейных уравнений
в комплексных числах и позволяющую рассчитать трехфазную цепь,
изображенную на рис. 5.
|
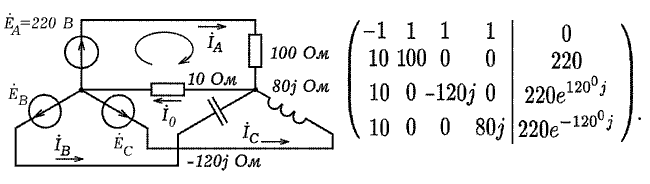
Рис. 5. Трехфазная цепь
Изучение трехфазных цепей предполагает нахождение комплексных значений
токов, что требует решения системы уравнений в комплексных числах.
По законам Кирхгофа составьте систему уравнений в комплексных числах.
Цепь имеет три независимых контура и два узла O и O', всего 4 ветви;
получаем систему из 4 независимых уравнений:
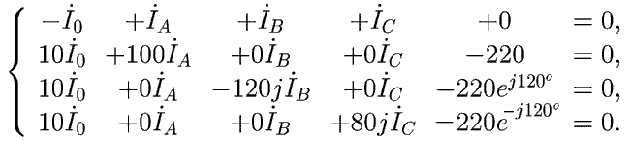
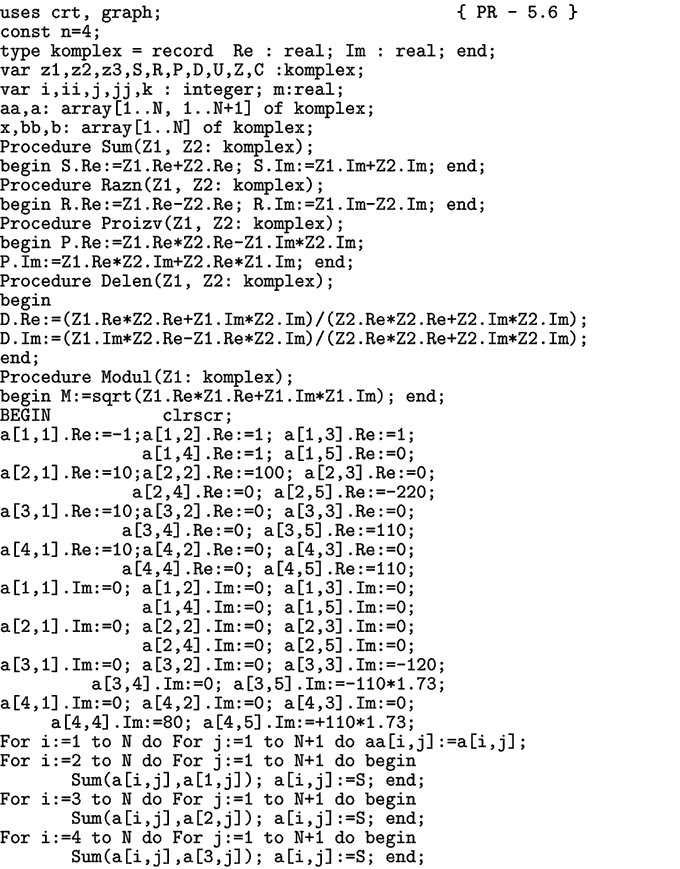
Эта системы уравнений может быть решена путем приведения матрицы
коэффициентов к треугольному виду. В используемой программе ПР-6
операции сложения, вычитания, умножения и деления комплексных чисел
осуществляются в процедурах Sum, Razn, Proizv, Delen.
Сначала, чтобы исключить деление на 0, складываются второе, третье и
последующие уравнения с первым. Делят элементы каждой строки матрицы на
первый элемент, после чего вычитают из второй, третьей и т.д. строк
первую. В результате первые элементы второй, третьей и последующих
строк оказываются равными 0. Аналогичным образом приводят к 0 вторые
элементы третьей, четвертой и последующих строк и т. д. Эти операции
повторяют до тех пор, пока матрица не будет приведена к треугольному
виду. Это позволяет вычислить искомые значения
комплексов токов и осуществить проверку решения. Эта программа может быть
использована для решения системы уравнений в действительных числах.
| 
|
Программа ПР-6.

Тексты программ находятся в zip-архиве,
файл gl-5.pas.
ВВЕРХ
Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс].
- Глазов: ГГПИ, 2012 //
Web-site http://maier-rv.glazov.net .
|