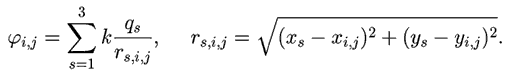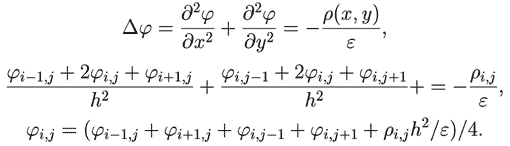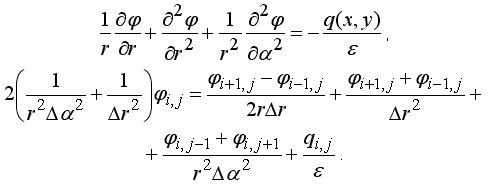РАСЧЕТ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
|
 |
Задача 1.
Три точечных заряда q1, q2, q3
имеют координаты (x1, y1),
(x2, y2), (x3, y3).
Рассчитайте потенциал электростатического поля во всех точках
плоскости, содержащей эти заряды.
|
В цикле будем перебирать все точки плоскости (пиксели экрана),
задаваемые целочисленными параметрами i и j. При этом будем
вычислять расстояния от данной точки до каждого заряда и находить
алгебраическую сумму потенциалов:
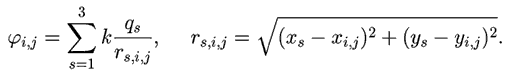
В зависимости от величины потенциала ставится точка
соответствующего цвета. Используется программа ПР-1,
результат моделирования -- на рис. 1.
| 
|
Программа ПР-1.
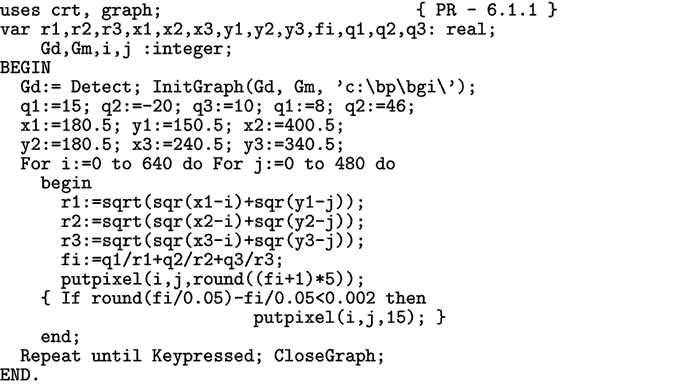

Рис. 1. Расчет потенциала поля точечных зарядов.
Рассмотренный метод может быть использован для расчета полей, созданных
протяженными заряженными телами. Например, чтобы промоделировать
электростатическое поле плоской пластины можно вместо нее расположить
10-20 точечных зарядов, лежащих на прямой. Программа ПР-2
рассчитывает поле пластины и расположенного рядом с ней точечного
заряда. Результат вычислений приведен на рис. 2.
| 
|
Программа ПР-2.


Рис. 2. Расчет потенциала поля точечных зарядов
 |
Задача 2.
Две пластины имеют потенциалы 100 В и -100 В. Между ними вблизи краев
находится металлический шарик с потенциалом 20 В. Рассчитайте
распределение потенциала. |
Расчет распределения потенциала электрического поля, созданного
протяженными заряженными телами, требует решения уравнения
Пуассона. Запишем его в конечных разностях:
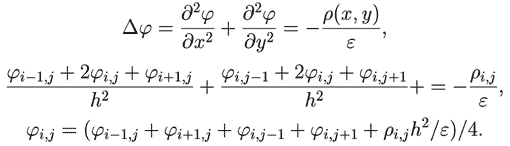
Для решения задачи используется программа ПР-3. Результат
расчета распределения потенциала представлен на рис. 3.
| 
|
Программа ПР-3.


Рис. 3. Моделирование электростатического поля
 |
Задача 3.
Необходимо рассчитать распределение потенциала в двумерной области,
решив уравнение Пуассона в полярных координатах. Потенциалы отдельных
точек и граничные условия заданы.
|
Это стационарная задача. Соответствующие дифференциальное
и конечно-разностное уравнения имеют вид:
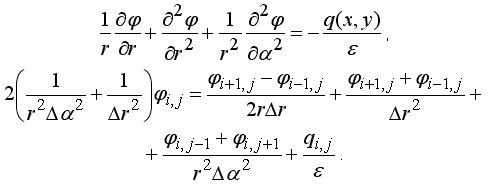
| 
|
Используется программа ПР-4. Результаты вычисления распределения потенциала
в двумерной области при некоторых граничных условиях представлены на рис. 4.
Программа выполняет последовательность итераций, получающиеся значения
потенциалов постепенно приближаются к искомым значениям, которые
соответствуют точному решению задачи (рис. 5).
Программа ПР-4.

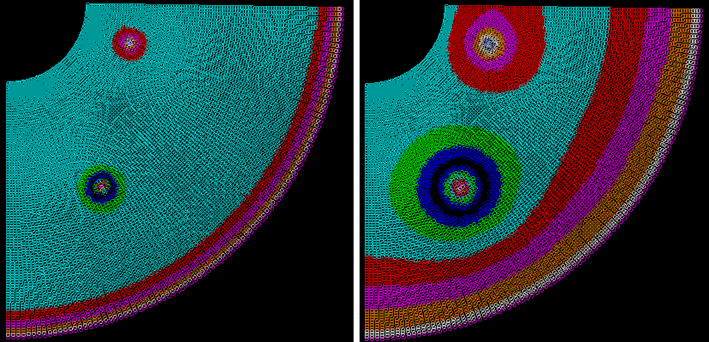
Рис. 4. Результаты рaсчетов после первых
нескольких сотен итераций.
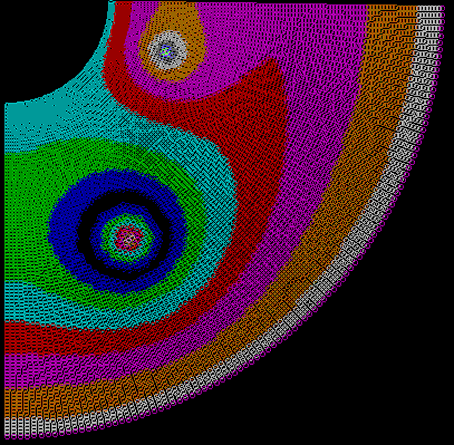
Рис. 5. Окончательный результат расчета
распределения потенциала.
Тексты программ находятся в zip-архиве,
файл gl-6.pas.
ВВЕРХ
Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс].
- Глазов: ГГПИ, 2012 //
Web-site http://maier-rv.glazov.net .
|