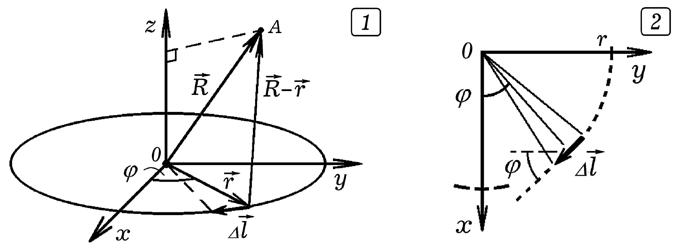
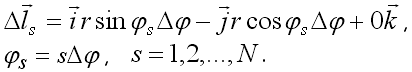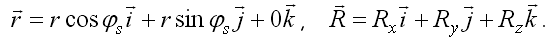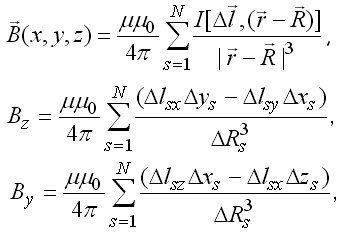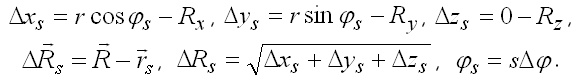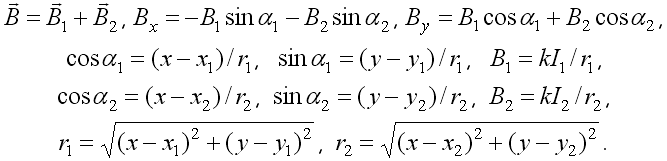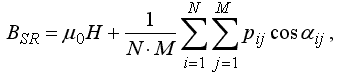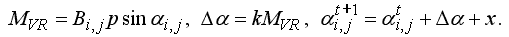Рис. 1. Магнитное поле витка с током.
По закону Био-Савара-Лапласа для вектора индукции и его проекций можно записать:
При этом используются формулы:
Используется программа ПР-1. Для построения силовой линии задают начальную точку A0, определяют в ней направление индукции магнитного поля, строят небольшой отрезок в направлении вектора индукции, переходя в новую точку A1. Затем повторяют все снова. Результаты вычислений -- на рис. 2, 3, 4. Программа ПР-1.
Рис. 2. Магнитное поле обмотки.
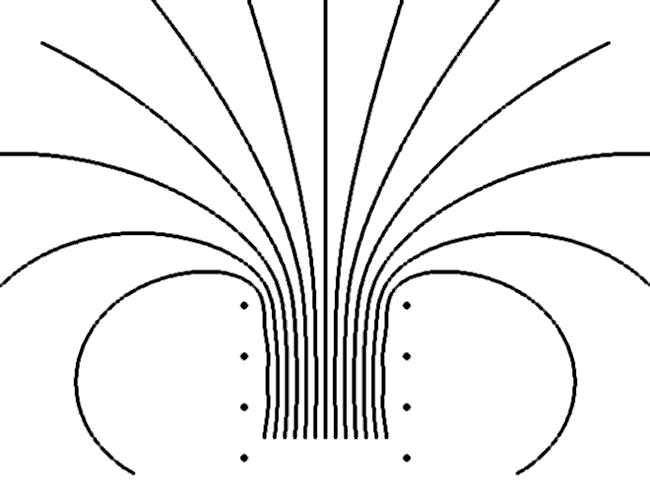
Рис. 3. Магнитное поле двух обмоток. Токи сонаправлены.
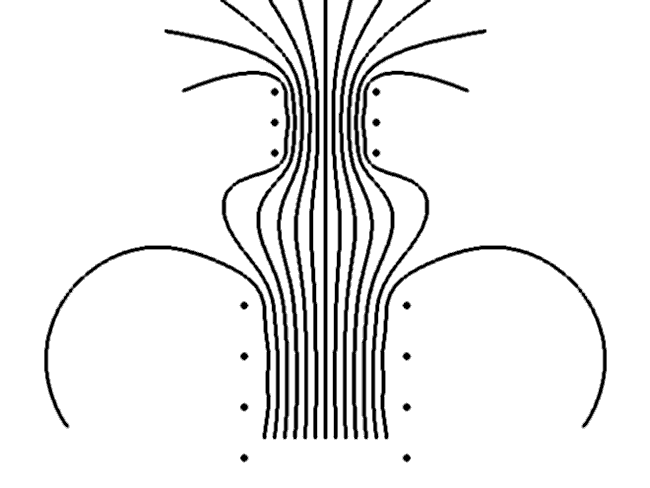
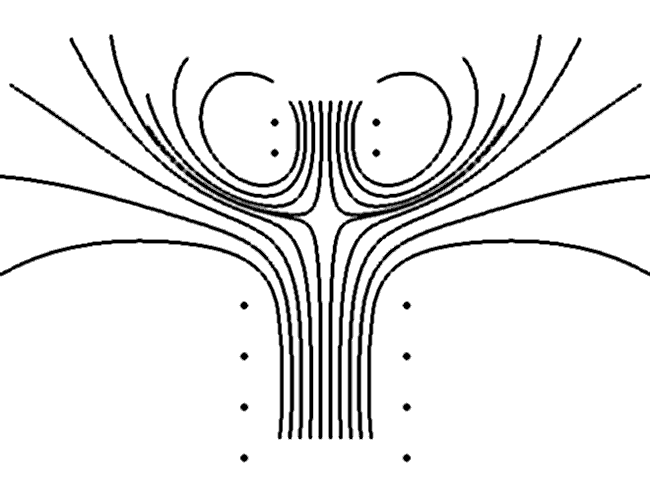
Рис. 4. Токи в обмотках направлены противоположно."
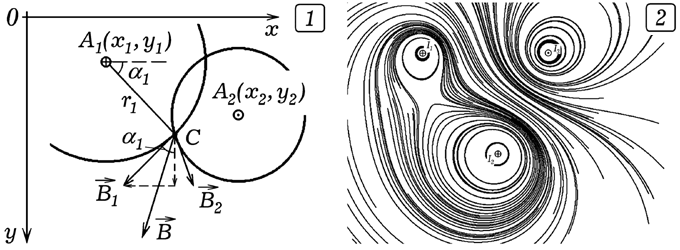
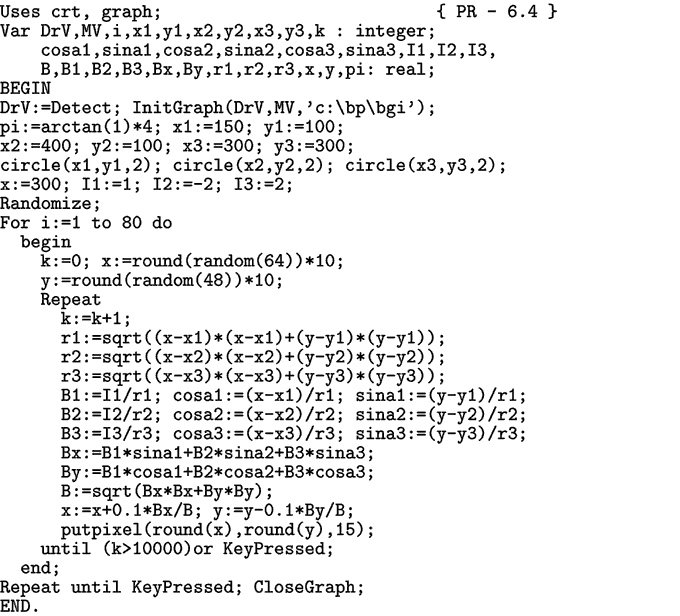
Рис. 5. Расчет магнитного поля двух токов. Допустим, два проводника с токами I1 и I2 пересекают плоскость XOY (рис. 5) в точках с координатами (x1,y1) и (x2,y2). Индукция магнитного поля в точке A(x,y) может быть найдена по формулам:
Используемая программа ПР-2 случайным образом выбирает точку A0, определяет проекции вектора индукции и в его направлении строит отрезок единичной длины, находя точку A1. Затем все повторяется снова (рис. 6). Выполнив 10000 шагов, программа снова случайно выбирает точку A0 и начинает строить вторую силовую линию и т.д. Программа ПР-2.
Рис. 6. Магнитное поле трех проводников с током
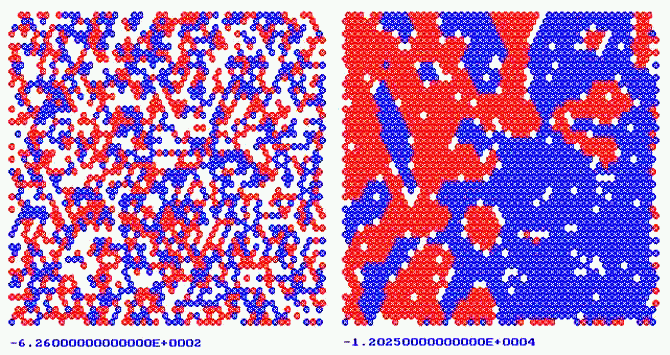
Процесс моделирования состоит в следующем: 1) задается начальная ориентация всех спинов случайным образом; 2) определяется энергия системы; 3) случайно выбирается один атом, и его спин изменяется на противоположный, определяется энергия системы в новой конфигурации; 4) если в результате переориентации спина энергия уменьшилась, то такое изменение конфигурации принимается, в противном случае - отклоняется; 5) результат выводится на экран; 6) возврат к операции 2. Для решения этой задачи используется программа ПР - 6.5, при этом моделируется ситуация, в которой в левом верхнем углу индукция магнитного поля направлена от нас, а в правом нижнем углу - к нам. Используется не квадратная, а шестиугольная сетка, результат вычислений - на рис. 7. Программа ПР-3.
Рис. 7. Модель ферромагнетика Изинга
где H -- напряженность магнитного поля, αij -- угол между вектором магнитного момента p и осью Ox. Индукция магнитного поля Bij в данном узле сетки обусловлена внешним полем обмотки μ0H и магнитным полем, создаваемым соседними атомами. В проекции на ось Ox:
Со стороны магнитного поля на атом, находящийся в узле (i, j), действует вращающий момент MVR. При повороте атома возникает момент "упругих сил", препятствующий повороту. В результате действия этих моментов, а также сил внутреннего трения, атом поворачивается на Δα. Запишем уравнения:
Здесь x -- небольшая случайная величина в интервале [-0,1; 0,1], учитывающая хаотические колебания атомов в узлах кристаллической решетки. Давая случайное приращение x углу α, мы "встряхиваем" нашу модель, предоставляем возможность найти более "удачные" значения α. Это важно еще и потому, что в анализируемой модели число атомов существенно меньше, чем в реальном ферромагнитном стержне. Суть вычислительного эксперимента состоит в плавном увеличении напряженности магнитного поля H и пересчете αij у всех атомов с нахождением соответствующих средних значений индукции магнитного поля B. В результате на плоскости B от H получится кривая намагниченности с характерным горизонтальным участком, соответствующим магнитному насыщению, когда магнитные моменты всех атомы ориентированы по полю. Для получения петли гистерезиса необходимо, чтобы напряженность поля H изменялась по гармоническому закону (рис. 8). Используемая программа ПР-4 содержит цикл по времени t, в котором пересчитываются H, αij, BSR и строится зависимость B(H).
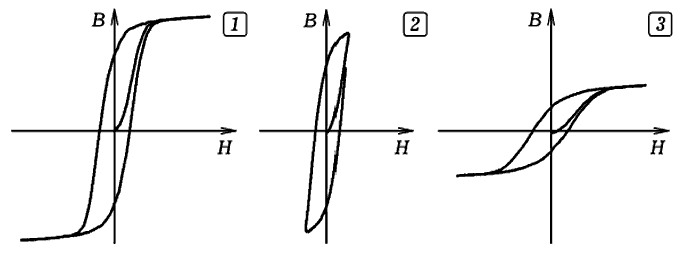
Рис. 8. Результаты моделирования магнитного гистерезиса. Программа ПР-4.
Необходимо запустить программу PR-4 и подождать пока на экране строится петля гистерезиса (рис. 8.1). Шаг по времени должен быть достаточно мал. При уменьшении амплитуды колебаний напряженности поля получается петля, изображенная на рис. 8.2.
Если уменьшить магнитный момент атомов p в несколько раз (от 3,4 до 1,4), то уменьшится индукция магнитного поля, соответствующая насыщению, петля гистерезиса сожмется по вертикали (рис. 8.3). Тексты программ находятся в zip-архиве, файл gl-61.pas. ВВЕРХ
Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net . |