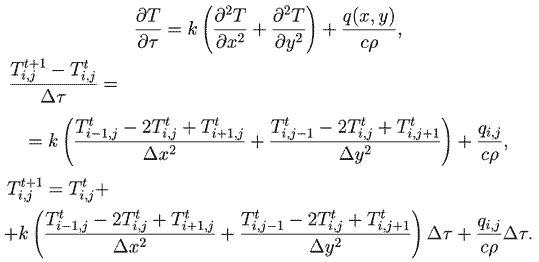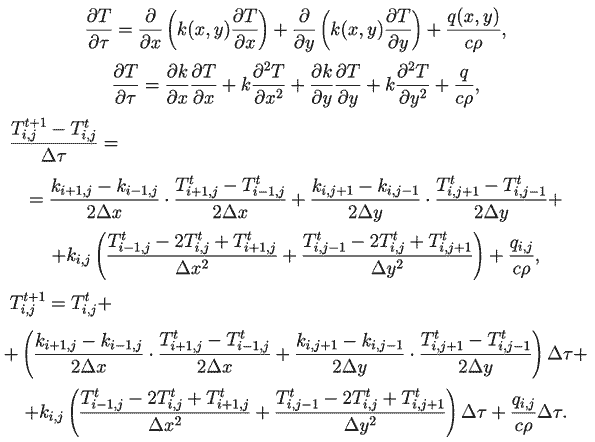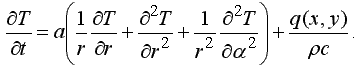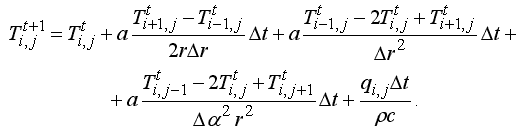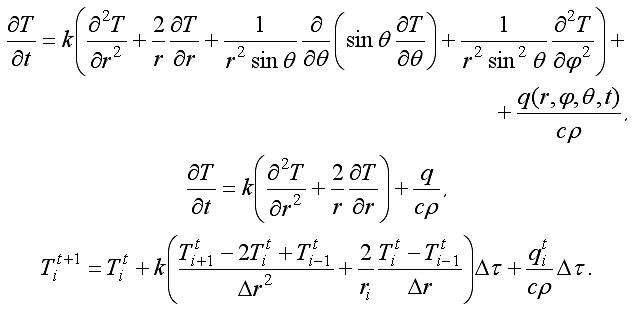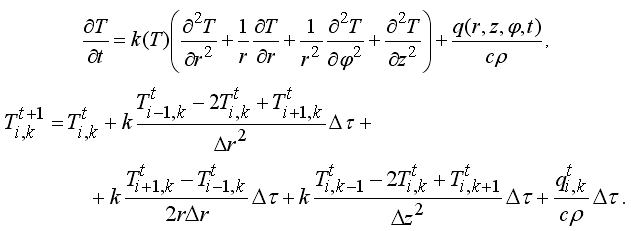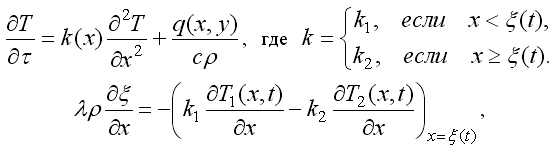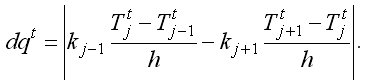Задача 1. Имеется пластина с прямоугольным отверстием. Правая сторона пластины теплоизолирована, остальные поддерживаются при постоянной температуре. В противоположных углах пластины расположены источник тепла и источник холода. Необходимо рассчитать распределение температуры в последовательные моменты времени.

Уравнение теплопроводности для двумерной среды в конечных разностях имеет вид:

Для расчета распределения температуры по поверхности пластины используется программа ПР-1. Она содержит цикл по времени с вложенными в него двумя циклами по i и по j, в которых перебираются все элементы пластины и вычисляются их температуры в последующие моменты времени. Результат решения задачи представлен на рис. 1, - на нем разными цветами изображены области с различными температурами. Изотермы (границы разноцветных областей) перпендикулярны теплоизолированным краям пластины и параллельны краям, температура которых поддерживается постоянной.

Программа ПР-1.

Рис. 1. Распределение температуры: двумерная среда.

Задача 2. Пластина состоит из трех полосок с различными коэффициентами теплопроводности. Нижняя сторона пластины теплоизолирована, остальные поддерживаются при постоянной температуре. В разных местах пластины расположены протяженный источник тепла и источник холода. Необходимо рассчитать распределение температуры в последовательные моменты времени.

Заменяя частные производные их конечно-разностными аппроксимациями, запишите уравнение теплопроводности для неоднородной двумерной среды в конечных разностях:

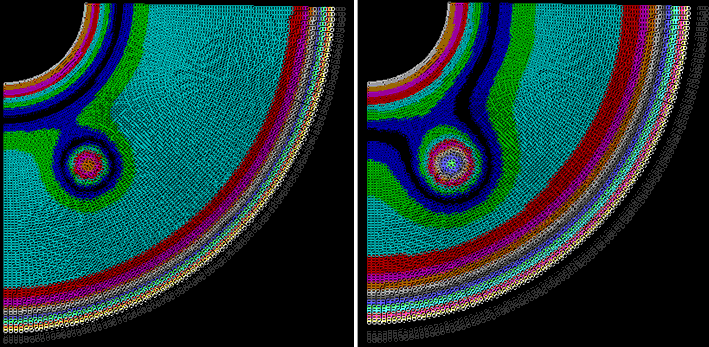
Для решения задачи используется программа ПР-2. В ней последовательно перебираются узлы двумерной сетки по строкам и по столбцам. Когда переменная naprav равна 0, то элементы перебираются по столбцам сверху вниз и снизу вверх. Когда переменная naprav равна 1, то элементы перебираются по строкам слева направо и справа налево. Нижний край пластины теплоизолирован, это задается циклом:

For i:=1 to N do t[i,M]:=t[i,M-1];

Все остальные края пластины поддерживаются при постоянной температуре. Результат работы программы представлен на рис. 2.

Программа ПР-2.

Рис. 2. Теплопроводность в неоднородной среде.

Задача 3. Имеется неоднородный стержень, известна начальная температура различных его точек, координаты и мощность источника тепла (холода). Один конец теплоизолирован, другой поддерживается при постоянной температуре. Необходимо рассчитать распределение температуры вдоль стержня.

Для решения задачи может быть использован алгоритм АЛ-1. Алгоритм АЛ-1 НАЧАЛО ПРОГРАММЫ ДЛЯ i:=1 ДО N ДЕЛАТЬ {- ЕСЛИ (i>18)И(i<22) ТО T[i]:=5 ИНАЧЕ T[i]:=0.1; -} ДЛЯ j:=1 ДО N ДЕЛАТЬ {- ЕСЛИ j>20 ТО k[j]:=1.8 ИНАЧЕ k[j]:=1; -} ПОВТОРЯТЬ ДО НАЖАТИЯ НА КЛАВИШУ {== kk:=kk+1; ДЛЯ i:=2 ДО N-1 ДЕЛАТЬ { ЕСЛИ (i>80) И (i<83) ТО q:=0.5 ИНАЧЕ q:=0; TT[i]:=T[i]+k[i]*(T[i+1]-2*T[i]+T[i-1])*dt/(h*h)+ (k[i+1]-k[i-1])*(T[i+1]-T[i-1])*dt/(4*h*h)+q*dt; } ДЛЯ i:=2 ДО N-1 ДЕЛАТЬ { T[i]:=TT[i]; } T[1]:=0.1; T[N]:=T[N-1]; ЕСЛИ kk/1000=round(kk/1000) ТО { ДЛЯ i:=2 ДО N ДЕЛАТЬ {- ПОСТАВИТЬ ТОЧКУ (i, T[i]); -} ==} КОНЕЦ ПРОГРАММЫ

В программе ПР-3 используются два массива T[i] и TT[i], в которых сохраняются значения температуры элементов стержня в моменты t и t+1 соответственно. Расчет температуры осуществляется по выведенной выше формуле в цикле. Будем считать, что длина стержня l, его коэффициент температуропроводности k при x>0,2l равен 1,8, а при x<0,2l равен 1. 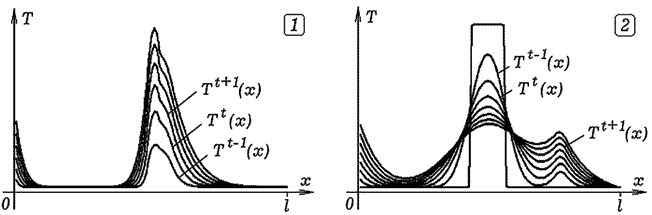Температура точек с координатами от 0,18l до 0,22l равна T₁; все остальные точки имеют температуру T₂1. Точки, координата x которых лежит в интервале от 0,81l до 0,82l, нагреваются источником тепла известной мощностью q. Левый конец поддерживается при постоянной температуре, а правый -- теплоизолирован. Результаты решения задачи при других начальных и граничных условиях представлены на рис. 3.

Программа ПР-3.

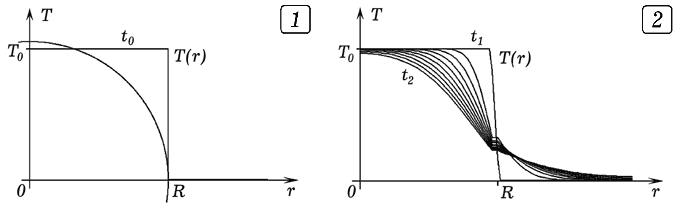
Рис. 3. Теплопроводность стержня.

Задача 4. Имеется однородная пластина, на которой расположены источник тепла и источник холода известной мощности. Один край пластины теплоизолирован, другой поддерживается при постоянной температуре. Необходимо решить уравнение теплопроводности в полярных координатах и рассчитать температуру в различных точках пластины.

Эта нестационарная задача требует решения следующего уравнения теплопроводности в полярных координатах: В конечных разностях получаем:

Программа ПР-4.

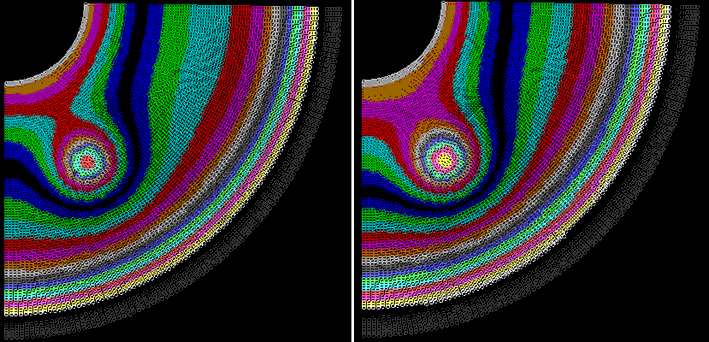
Для решения этой задачи используется программа ПР-4. Он содержит два вложенных цикла по i и j, в которых перебираются все узлы двумерной сетки и пересчитываются значения T[i,j] на следующем временном слое. При ее запуске на экране появляется цветное изображение, границы одноцветных областей соответствуют изотермам. Пример результата вычислений приведен на рис. 4.

Рис. 4. Решение уравнения теплопроводности в полярных координатах.

Задача 5. Металлический шар нагрели до температуры T0, а потом опустили в вязкую жидкость (конвекция отсутствует), имеющую температуру T1. Шар некоторое время охлаждается, температура его поверхности уменьшается. После этого шар вынули из жидкости и поместили в газообразную среду с низкой теплопроводностью. За счет теплообмена с центральной частью шара температура его поверхности повышается, а температура в центре понижается. Через некоторое время из–за теплообмена с газообразной средой температура поверхности начинает медленно уменьшаться, шар охлаждается. Необходимо рассчитать температуру различных точек шара и среды в последовательные моменты времени.

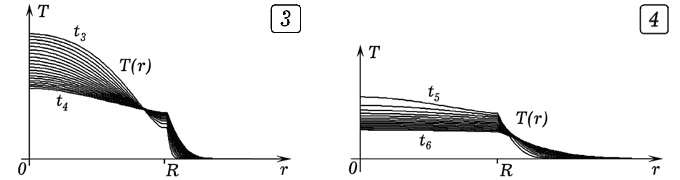
Запишем уравнение теплопроводности в сферических координатах, учитывая, что поле температур не зависит от меридиональной и азимутальной координат; перейдем к конечным разностям:

При решении задачи следует учесть граничные условия сопряжения: если между двумя телами (шаром и вязкой средой) имеется идеальный тепловой контакт, то: 1) их температуры на поверхности контакта одинаковы; 2) по закону сохранения энергии тепловой поток, выходящий из шара, равен тепловому потоку, входящему в среду.

Используется программа ПР–5. Чтобы учесть граничные условия сопряжения, введем функцию q(t), учитывающую теплопередачу от шара к среде. Будем считать, что на поверхности шара (точка с координатой r=R) имеется поглотитель тепла с отрицательной мощностью α(T_п-T_с), а в ближайшей точке среды имеется источник тепла с той же по модулю мощностью. Здесь T_п и T_с –– температуры поверхности шара и прилегающего к ней слоя среды, α –– коэффициент теплоотдачи.

Программа ПР-5.

На рис. 5.1 показано начальное распределение температуры. Пока шар находится внутри жидкости, он охлаждается (рис. 5.2), температура поверхности становится ниже, чем в центре. Когда шар помещают в воздух, то температура поверхности повышается за счет теплообмена с центральной частью шара; теплообмен с окружающей средой происходит существенно медленнее (рис. 5.3). Через некоторое время температура поверхности шара начинает уменьшаться за счет теплообмена с окружающей средой (рис. 5.4). Если жидкость, в которую опускают нагретый шар, имеет небольшую вязкость, то возникают конвективные потоки. При этом можно приближенно считать, что температура всех точек жидкости одинакова и равна некоторой средней температуре T_ср. Решение задачи упрощается.

Рис. 5. Результаты расчета поля температур при охлаждении шара.

Задача 6. В тонкостенном цилиндрическом сосуде находится жидкой парафин при температуре T выше температуры отвердевания TK. Сосуд опускают в большой резервуар, наполненный холодной водой. Происходит охлаждение, парафин отвердевает, при этом в центре его верхней поверхности образуется углубление. Необходимо рассчитать поле температур в последовательные моменты времени.

Допустим, в сосуде находится некоторое гипотетическое вещество, которое при охлаждении отвердевает (или кристаллизуется) и уменьшает свой объем на 2–5 %. При этом возникает граница раздела двух фаз (фронт отвердевания), сжимающаяся к центру сосуда. На уже отвердевшие слои у края сосуда натекает жидкость из центральной более горячей части и тоже отвердевает. Поэтому в центре сосуда образуется углубление. Если вещество при кристаллизации расширяется (например, как вода), то в центре сосуда появляется выпуклость.

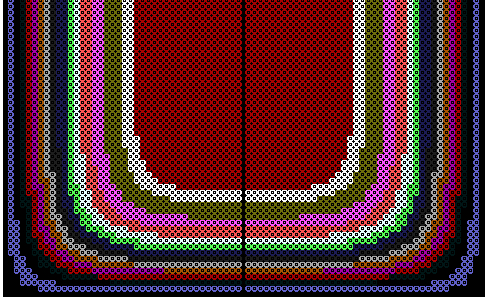
При кристаллизации происходит выделение энергии; чтобы это учесть, будем считать, что в узлах, температура которых примерно равна температуре кристаллизации, появляются источники тепла определенной мощности. Более точное решение требует записи условия Стефана.

В силу симметрии поле температур не зависит от φ. Запишем уравнение теплопроводности в цилиндрической системе координат и конечных разностях:

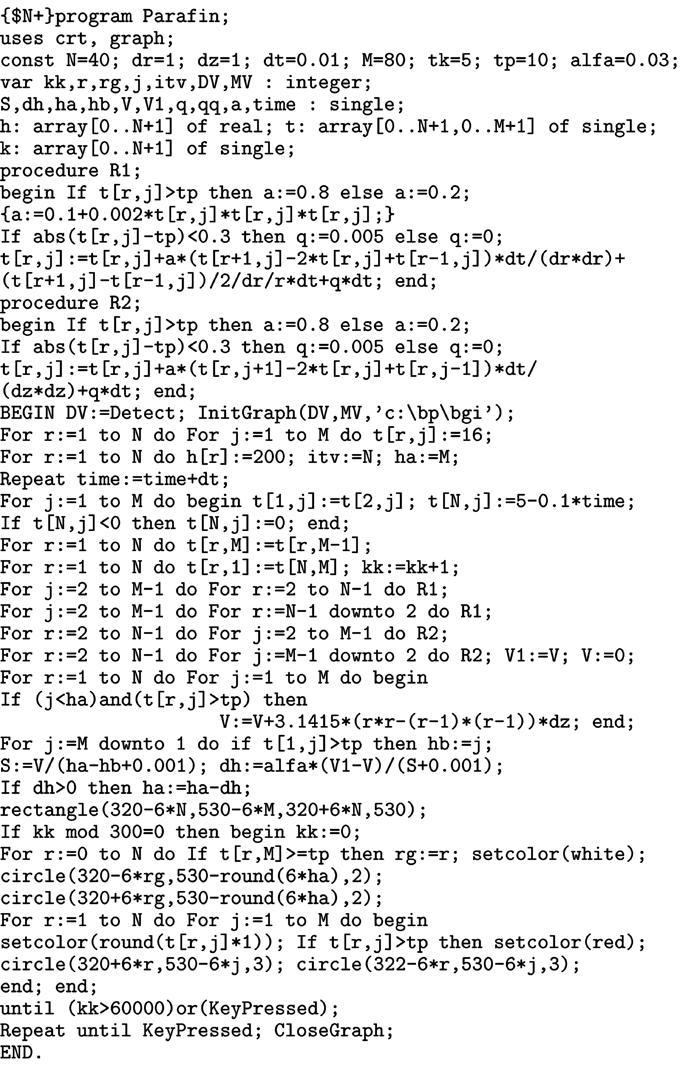
Для расчета нестационарного поля температур на следующем временном слое организуют два цикла по i и j, в которых рассчитываются температура в узлах сетки (процедуры R1 и R2) сначала в одном, а потом в другом направлениях. На экране рисуется половина осевого сечения цилиндрического сосуда с помощью точек, цвет которых зависит от температуры. Та часть вещества, которая находится в жидком состоянии (T больше T_K) изображается красным цветом. По мере охлаждения эта область постепенно уменьшается и исчезает.

Чтобы рассчитать форму поверхности отвердевшего вещества, необходимо определить объем его жидкой фазы в произвольный момент времени . Это делается с помощью цикла:

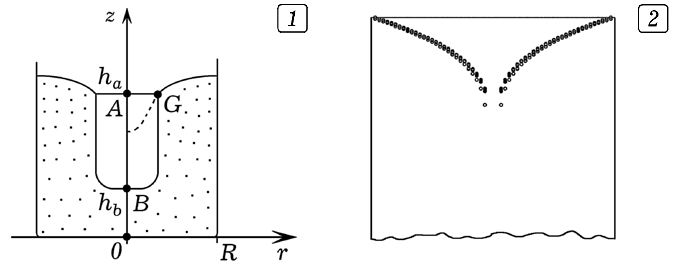
Рис. 6. Образование углубления при отвердевании парафина.

Здесь учтено, что объем кольца с внешним радиусом r и внутренним r-Δr и высотой Δz равен 3,14*(r²-(r-Δr)²)Δz. Зная значение V в предыдущий момент времени t-1, можно найти объем вещества, затвердевшего в течение последнего шага по времени: ΔV=V^t-1-V^t. Обозначим высоты верхней и нижней точек расплавленной области через h_a и h_b (рис. 6.1), тогда эффективная площадь горизонтального сечения S расплавленной области S=V/(h_a-h_b). Так как объем вещества за счет кристаллизации уменьшился на αΔV, то высота h_b уменьшится на Δh=αΔV/S, где α=0,02–0,05. Программа может нарисовать горизонтальную прямую AG, где G –– точка на высоте h_a, в которой жидкая фаза переходит в твердую.

Программа ПР-6.

Используется программа ПР–6; результаты расчета формы поверхности представлены на рис. 6.2. Видно, что в центральной части сосуда образуется углубление. Этот результат устойчиво получается и при небольших вариациях параметров системы. Можно усложнить модель и учесть, что коэффициент теплопроводности вещества в жидком состоянии существенно больше, чем в твердом. Например, в узлах сетки, для которых T больше T_K, коэффициент теплопроводности k=0,8, а в остальных узлах k=0,2. При этом получаются аналогичные результаты (рис. 6.2 и 7). Модель имеет несущественный недостаток: при решении уравнения теплопроводности мы пренебрегаем искривлением верхней границы расчетной области, считая ее горизонтальной плоскостью. Учет этого фактора приведет к изменению поля температур; изотермы останутся перпендикулярны верхней искривленной границе, решение задачи в центральной области будет более точным.

Рис. 7. Поле температур при остывании вещества в цилиндрическом сосуде.

Задача 7. Рассмотрим одномерную двухфазную задачу Стефана. Имеется одномерная теплопроводящая среда, находящаяся в жидком и твердом состояниях. В начальный момент ее температура меньше температуры плавления Tпл. В точках с координатами x меньше 2 имеются источники тепла, под воздействием которых происходит плавление на границе раздела фаз, протекающее при температуре Tпл. Необходимо найти распределение температуры в последовательные моменты времени и определить расположение границы фаз.

Компьютерные модели распространения тепла в средах с изменяющимся фазовым состоянием представляют особый интерес. Среди них задача о промерзании грунта (решена Стефаном 1889 г.), задача о кристаллизации расплава при погружении в него пластины, задача о нарастании ледяного покрова, металлургическая задача об остывании расплавленных тел и образовании слитка, задача об отвердевании земного шара из расплавленного состояния и другие.

Задача сводится к решению уравнения теплопроводности совместно с условием Стефана, вытекающего из уравнения теплового баланса:

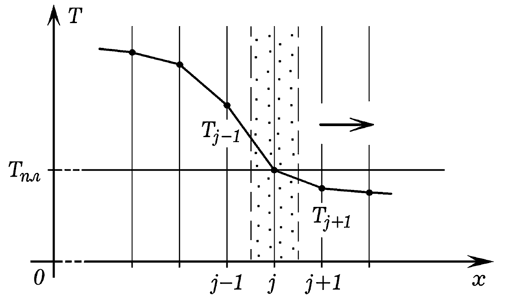
где λ –– удельная теплота плавления, ρ –– плотность среды, x=ξ(t) –– уравнение границы разделяющей жидкую и твердую фазы, k₁, k₂ –– коэффициенты температуропроводности жидкой и твердой фазы соответственно, T₁ и T₂ –– температуры вблизи границы раздела x=ξ(t) со стороны жидкой и твердой фаз.

Рассмотрим решение задачи Стефана для одномерной среды длиной L, когда температура левого конца все время выше T_пл, правый конец теплоизолирован, а граница раздела фаз смещается вправо (рис. 8). На каждом шаге определяется число узлов j, для которых T_i больше T_пл (i не превосходит j). Температура в j–том узле незначительно отличается от температуры плавления T_пл, поэтому переменной T_j присваивается значение T_пл. Количество теплоты, приходящее в j-тый узел, на шаге t

Здесь k_j-1 и k_j+1 –– коэффициенты температуропроводности слева и справа от границы раздела двух фаз.

Рис. 8. Одномерная двухфазная задача Стефана.

Если количество теплоты dq^t, поступающее в j-тый слой, меньше заданного значения теплоты плавления q_пл=λρΔx, которую необходимо затратить, чтобы расплавить слой толщиной h=Δx единичной площади, то фронт плавления не смещается. ЭВМ вычисляет температуру в 2, 3, ..., (j-1)-том, а затем в (j+1), (j+2), ..., (N-1)-ом узлах. Температура T_j остается равной T_пл; значение dq^t накапливается в переменной dq. Если dq^t превышает q_пл, то j–тый слой плавится, и граница раздела жидкой и твердой фаз смещается вправо на 1 узел. Величина dq^t уменьшается на затраченную энергию q_пл. Переменной T_j+1 присваивается значение T_пл, и все повторяется снова.

Программа ПР-7.

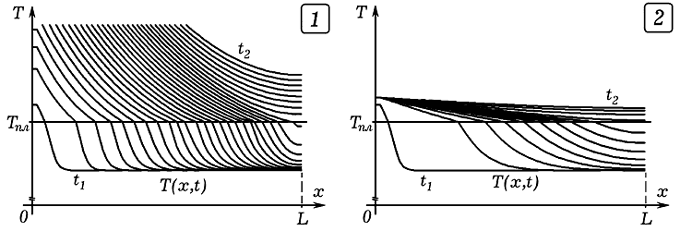
Рассмотренный алгоритм реализован в программе ПР–7. В нашем случае теплопроводность жидкой фазы в раза больше, чем у твердой фазы. На рис. 9.1 показаны получающиеся распределения температуры в последовательные моменты времени, если температура левого конца одномерной среды непрерывно растет. На рис. 9.2 приведен результат, соответствующий ситуации, при которой температура левого конца стержня повышается до некоторой величины, а затем остается постоянной. В обоих случаях время плавления зависит от количества теплоты q_пл, необходимого для плавления слоя толщиной h=Δx единичной площади, взятого при температуре плавления.

Рис. 9. Моделирование плавления стержня.

Рассмотренные выше задачи в общем–то известны; методика их решения изложена в научной и учебной литературе. Некоторые из них обсуждались профессором В.А.Сараниным на конференции “Учебный физический эксперимент: Проблемы и решения”, проводимой в Глазовском педагогическом институте. Решение других задач можно найти в Интернете.

Тексты программ находятся в zip-архиве, файл gl-7.pas.

Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net .