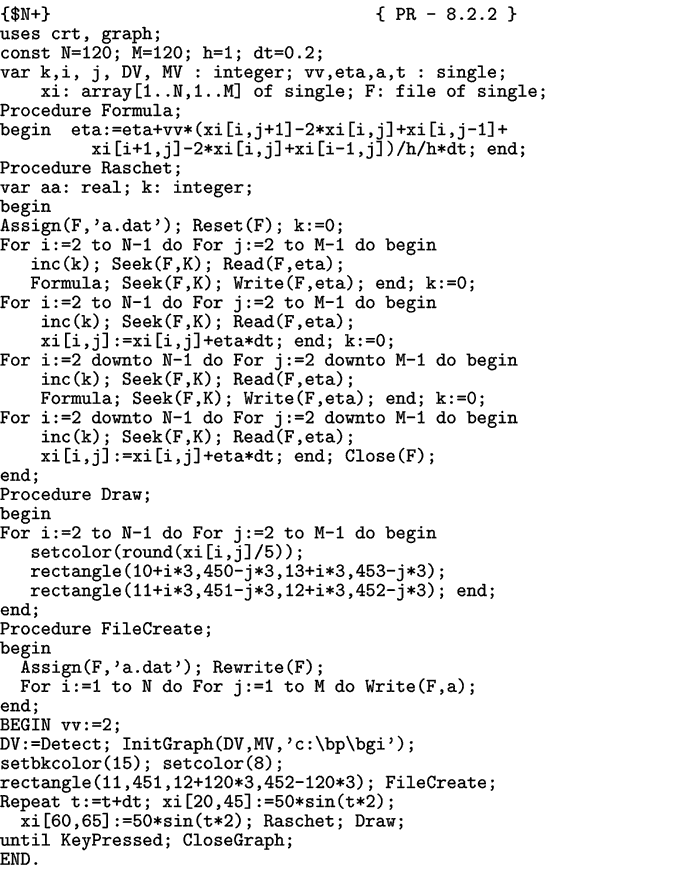
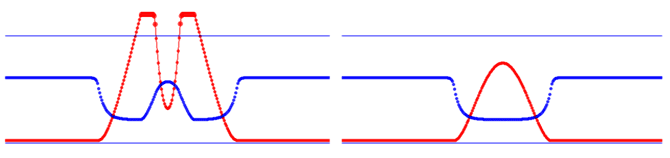
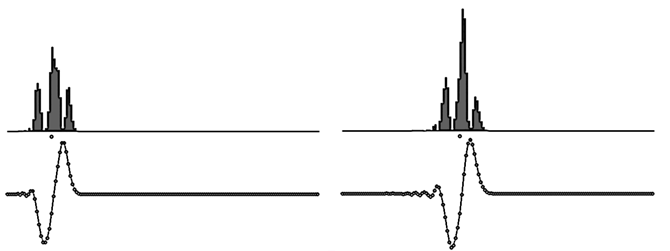
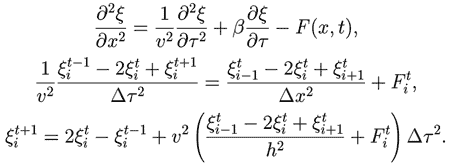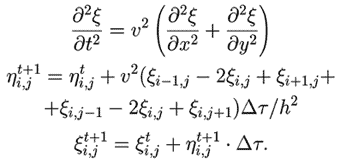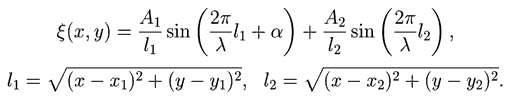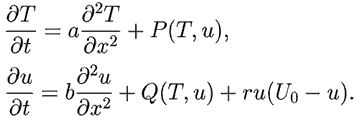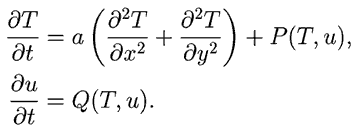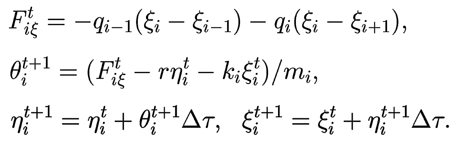Для получения движущегося профиля волны необходимо организовать цикл по i, в котором перебираются все элементы среды, вычисляются их смещения из положения равновесия. После этого стирается предыдущая моментальная фотография волны и строится новая. Все это должно находиться внутри цикла по времени (программа ПР-1). Результат моделирования прохождения волны через границу раздела двух сред приведен на рис. 1. Программа ПР-1.
Рис. 1. Одномерная волна: отражение и прохождение через границу раздела двух сред
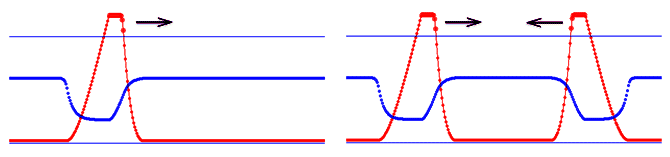
Для решения задачи используется программа ПР-2. Чтобы увеличить число узлов сетки, на которую разбита прямоугольная пластина, используются указатели. В двумерном массиве xi[i,j] хранятся значения смещения различных элементов среды (xi(i,j)^) и их скорости (xi(i+N,j)^) в формате single (4 байта). Чтобы исключить влияние волн, отраженных от края пластины, искусственно создается эффект затухания. Коэффициент затухания волн вблизи краев пластины считается равным r=0,2. Директива компилятора {$N+} необходима, чтобы включить математический сопроцессор. Результат моделирования прохождения волны через границу раздела двух сред приведен на рис. 2. Программа ПР-2.
Рис. 2. Моделирование волны в двумерной среде В представленной ниже программе ПР-3 использован другой прием: часть данных (скорости элементов среды eta) записывается в файл a.dat. Это позволяет увеличить число элементов массива xi[i,j]. Программа ПР-3.
Программа ПР-4.
Рис. 3. Интерференционная картина
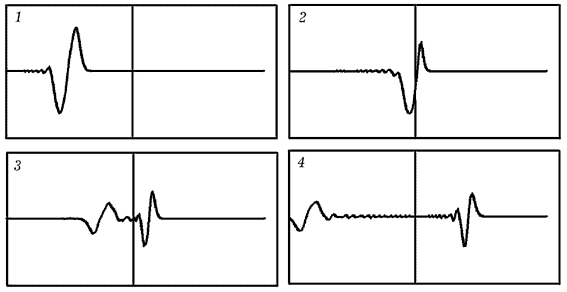
Изменение концентраций активатора и ингибитора описывается уравнением теплопроводности (диффузии). Используйте следующую математическую модель:
Когда трава горит (t[i]>tkr и u[i]>ukr), выделяется энергия (P=2), а количество травы уменьшается (Q=-0,07). Если трава сгорела, но температура элемента активной среды еще высока (t[i]>0), температура должна быстро уменьшаться за счет охлаждения (P=-0,1). Когда элемент среды охладился (t[i]<0.2), а трава не выросла (u[i]>u0), она растет, что описывается слагаемым r*u[i]*(u0-u[i]), где r=0,003. При горении температура травы не может превышать 1,2 tkr. Для численного решения рассмотренной выше системы двух дифференциальных уравнений необходимо заменить производные их конечно-разностными аппроксимациями и выразить t[i] и u[i] в дискретный момент времени t+1. Используется программа ПР-5. На рис. 4 и 5 представлены результаты моделирования распространения автоволны в одномерной среде и аннигиляции двух автоволн. Программа ПР-5.
Рис. 4. Распространение одномерной автоволны
Рис. 5. Аннигиляция одномерных автоволн
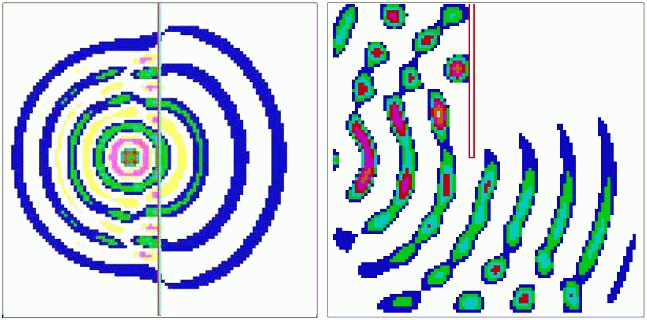
Разобьем прямоугольную область на элементы, каждый из которых характеризуется величинами T[i,j] и u[i,j]. С целью увеличения числа элементов подключите математический сопроцессор, переменную T[i,j] объявите, как single, а u[i,j] как word. Используется программа ПР-6, результаты моделирования представлены на рис. 6 и 7. Чтобы получить сферическую волну, элементы внутри круга небольшого радиуса переводят в возбужденное состояние, то есть "поджигают", задавая их начальную температуру достаточно высокой. Из рис. 6 видно, как образовавшаяся автоволна огибает препятствие (группу элементов черного цвета с низкой теплопроводностью). Для получения спиральной однорукавной автоволны задают фронт волны, оборванный в центре экрана (рис. 7). Программа ПР-6.
Рис. 6. Огибание сферической автоволной препятствия
Рис. 7. Однорукавная спиральная автоволна
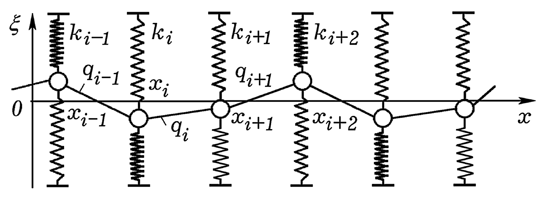
Рис. 7. Модель одномерной упругой среды
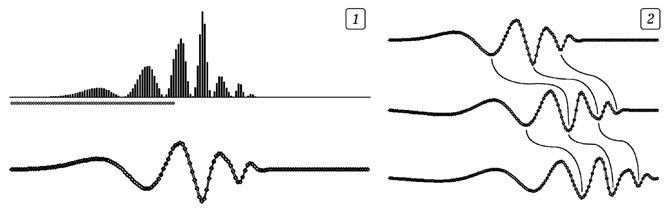
Ниже представлена программа ПР-7, моделирующая распространение импульса по цепочке осцилляторов, связанных упругими связями. Она содержит цикл по времени t и вложенный в него цикл по i, в котором последовательно перебираются все осцилляторы и вычисляются их ускорения, скорости и смещения. Тут же определяется кинетическая и потенциальная энергия колеблющихся осцилляторов. На экране строится "моментальная фотография волны" (зависимость смещения ξ от координаты x в фиксированный момент времени t) и зависимость энергии осцилляторов от координаты x. Эта компьютерная модель позволяет пронаблюдать распространение импульса, его отражение от края упругой среды, от "границы раздела двух сред". В случае, когда k = 0, импульс распространяется, не изменяя своей формы, его фазовая скорость (быстрота переноса колебаний) и групповая скорость (быстрота переноса энергии) равны (рис. 8). Если жесткость k и массу m осциллятора подобрать так, чтобы частота волны w была бы близка к его собственной частоте колебаний, то произойдет дисперсия. Импульс растягивается, фазовая скорость заметно отличается от групповой (рис. 9). Ниже приведен другой вариант программы (ПР-8) и результат ее использования (рис. 10). Программа ПР-7.
Рис. 8. Дисперсия отсутствует. Групповая и фазовая скорости равны
Рис. 9. Групповая скорость меньше фазовой. Имеет место дисперсия Программа ПР-8.
Рис. 10. Перемещение фазы волны в диспергирующей среде Тексты программ находятся в zip-архиве, файл gl-8.pas. ВВЕРХ
Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net . |