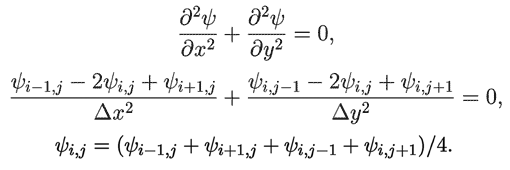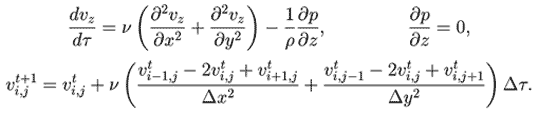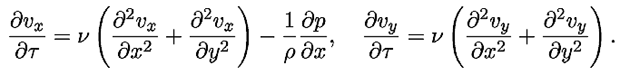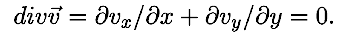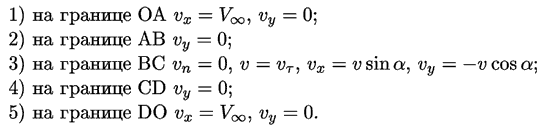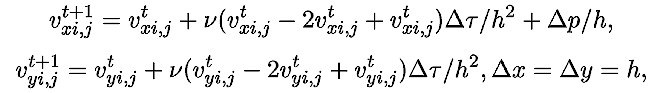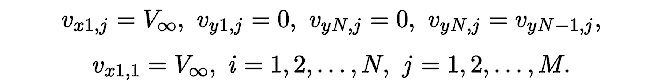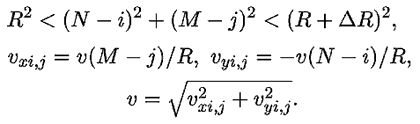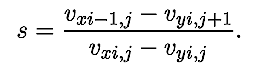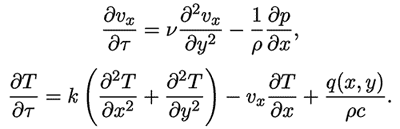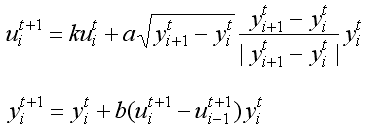НЕВИХРЕВОЕ ТЕЧЕНИЕ ЖИДКОСТИ
Задача 1.

Изучите установившееся потенциальное течение идеальной жидкости по трубе прямоугольного сечения. Внутри трубы имеются выступы и различные препятствия. Постройте линии тока.

Функция тока, характеризующая потенциальное течение жидкости, удовлетворяет уравнению Лапласа. Запишите его в конечных разностях:

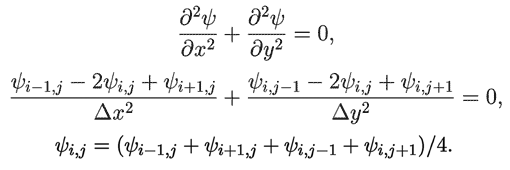
Для решения задачи используется программа ПР-1. Результаты расчета функции тока представлены на рис. 1 и 2.

Программа ПР-1.

Рис. 1. Результаты расчета потенциального течения.

Рис. 1. Результаты расчета потенциального течения.

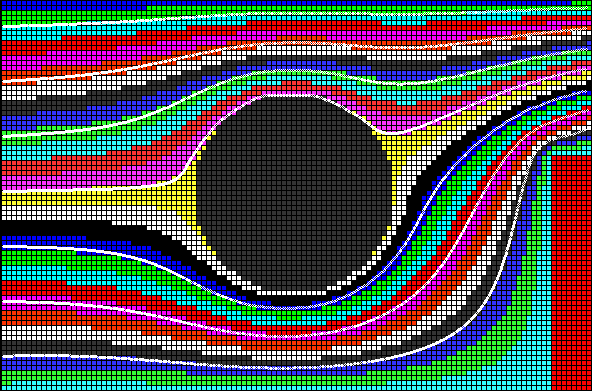
Рис. 2. Расчет линий тока потенциального течения.

Рис. 2. Расчет линий тока потенциального течения.

Задача 2.

Исследуйте установившееся безвихревое течение вязкой жидкости в длинной трубе (канале) постоянного сечения, внутри которой движется бесконечно длинное тело.

Это течение инвариантно по отношению к переносам в направлении движения. Для его расчета следует определить скорости в сечении, перпендикулярном направлению течения (оси z), т. е. решить уравнение:

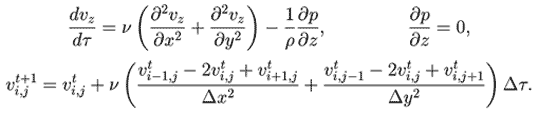
Используется программа ПР-2. Необходимо правильно задать граничные условия. Слои вязкой жидкости, прилегающие к поверхности твердого тела, имеют одинаковую с ним скорость. Если жидкость имеет свободную поверхность, то скорость частиц этой поверхности равна скорости частиц, расположенных слоем ниже. Результаты расчета обтекания длинного корпуса корабля и катамарана (рис. 3).

Программа ПР-2.

Рис. 3. Течение вязкой жидкости.

Рис. 3. Течение вязкой жидкости.

Задача 3.

Рассчитайте течение вязкой жидкости в бесконечно длинной трубе произвольного сечения при наличии разности давлений на концах трубы.

Задача 4.

Поток вязкой несжимаемой жидкости набегает на бесконечно длинный цилиндр. Течение ламинарное. Рассчитайте поле скоростей, постройте линии тока.

Поле скоростей симметрично относительно вертикальной и горизонтальной плоскостей, проходящих через ось цилиндра. Поэтому достаточно рассчитать поле скоростей в одном квадранте декартовой системы координат XOY. Из уравнений Навье-Стокса для несжимаемой жидкости для двумерного поля скоростей:

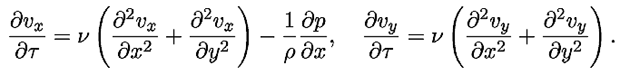
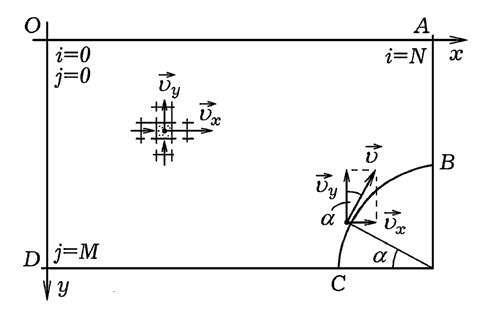
Рис. 4. К расчету поля скоростей в потоке вязкой жидкости.

Рис. 4. К расчету поля скоростей в потоке вязкой жидкости.

Так как отсутствуют источники, то

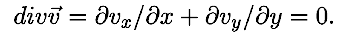
Расчет течения сводится к нахождению распределения скоростей, удовлетворяющему записанным дифференциальным уравнениям и граничным условиям (рис. 4):

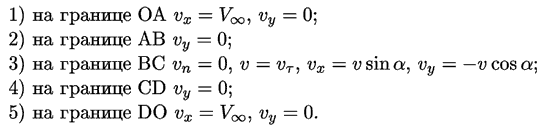
В конечных разностях получаем:

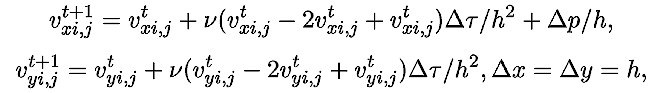
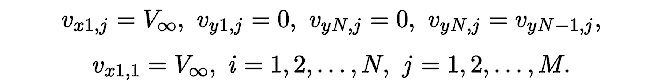
Так как во всех узлах сетки vx неотрицательно, vy неположительно, то из равенства дивергенции вектора скорости нулю следует, что vx,i,j - vy,i,j = vx,i-1,j - vy,i,j+1. В самом деле, суммарный поток вектора скорости через нижнюю и левую стенки квадратной ячейки должен быть равен суммарному потоку через верхнюю и правую стенки. Для границы CB должно выполняться:

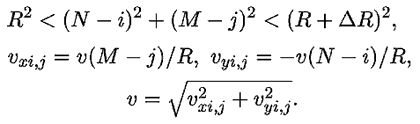
Используемая программа ПР-3 содержит вложенные циклы по i и j, в которых перебираются все узлы двумерной сетки и вычисляются значения проекций скорости. Затем отдельно для каждого узла находится коэффициент:

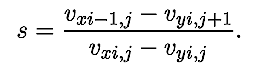
и пересчитываются проекции скорости так, чтобы дивергенция вектора скорости равнялась нулю. В процессе расчета поля скоростей программа строит векторы скорости в узлах сетки (процедура Draw1). Чтобы нарисовать линии тока в левую часть вводятся маркеры, которые смещаются в направлении течения жидкости (процедура Draw2).

Программа ПР-3.

Рис. 5. Обтекание цилиндра вязкой жидкостью.

Рис. 5. Обтекание цилиндра вязкой жидкостью.

Задача 5.

Между двумя горизонтальными пластинами течет без завихрений вязкая жидкость. Внутри потока имеется источник тепла известной мощности. Гравитационное поле отсутствует. Необходимо рассчитать поле скоростей и температур.

Рассмотрите двумерный поток вязкой жидкости, в котором находятся источники тепла. Ось Ox направим в направлении течения, а ось Oy – перпендикулярно пластинам. Распределение скоростей и температур может быть найдено из уравнений переноса:

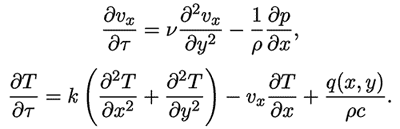
Для моделирования этого явления используется программа ПР-4, содержащая цикл по времени, в котором сначала рассчитывается поле скоростей (первые 300 итераций), а затем поле температур (рис. 6).

Программа ПР-4.

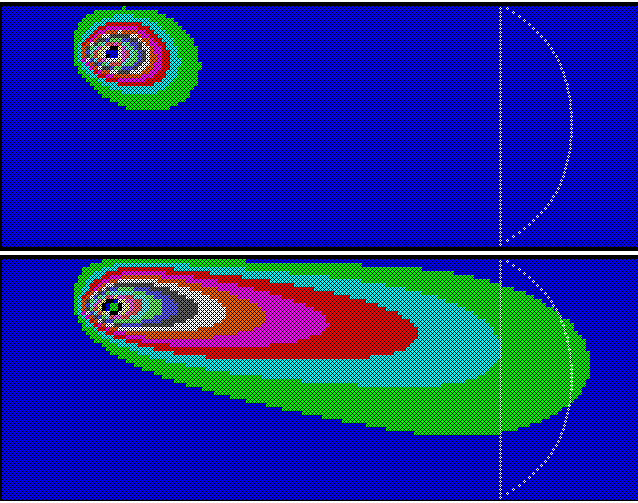
Рис. 6. Результаты расчета поля температур и скоростей.

Рис. 6. Результаты расчета поля температур и скоростей.

Задача 6.

В прямоугольном сосуде находится жидкость. Высота свободной поверхности жидкости зависит от координаты x следующим образом: y=h(x). В момент t=0 систему предоставляют самой себе, а в момент t' открывают отверстие в дне у левого края сосуда. Необходимо рассчитать форму свободной поверхности жидкости в последующие моменты времени.

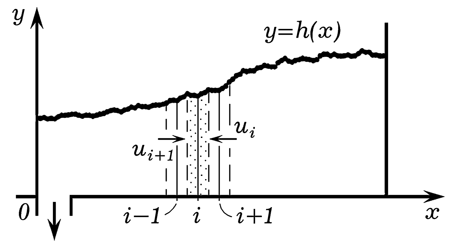
Рис. 7. К расчету формы свободной поверхности жидкости.

Рис. 7. К расчету формы свободной поверхности жидкости.

Рассмотрим двумерный сосуд, наполненный жидкостью, свяжем с ним систему координат XOY (рис. 7). Мысленно разрежем жидкость на N вертикальных слоев; высота i-того слоя (i= 1, 2, ..., N) равна yi=h(xi). Объем жидкости, проходящий через границу i-того и (i+1)-ого слоев обозначим через ui. Будем исходить из того, что объем жидкости, проходящий через границу i-того и (i+1)-ого слоев пропорционален квадратному корню из разности yi+1-yi и высоте уровня yi. Необходимо учесть инертность жидкости, а также то, что уровень yi на следующем шаге t+1 пропорционален разности объемов, втекающих в i-тый слой слева и справа. В результате получаем приближенную модель, которая имитирует колебания уровня жидкости в сосуде, образование и распространение поверхностных волн и т.д.:

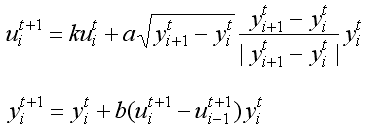
Программа ПР-5.

Используется программа ПР-5. На рис. 8 представлены результаты расчетов формы свободной поверхности жидкости в некоторые моменты времени. Объем жидкости в сосуде уменьшается за счет ее вытекания из отверстия в дне. Чтобы промоделировать, необходимо на каждом шаге t уменьшать уровень жидкости yi над отверстием на величину, пропорционлаьную квадратному корню из yi.

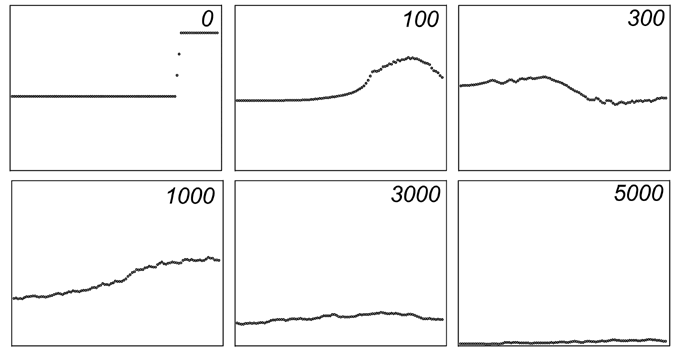
Рис. 8. Свободная поверхность жидкости в последующие моменты времени.

Рис. 8. Свободная поверхность жидкости в последующие моменты времени.

Задача 7.

Имеется прямоугольный резервуар, в дне которого у левой и правой стенок имеются отверстия, через которые может поступать вода. В начальный момент t=0 в резервуар через левое отверстие начинает поступать вода с постоянной скоростью (объемный расход Q1). В момент t' открывается второе отверстие, расположенное у правой стенки резервуара, и вода начинает через него вытекать (объемный расход Q2 зависит от высоты уровня воды). Необходимо расчитать форму свободной поверхности жидкости y=h(x) в различные моменты времени.

Задача решается аналогично. Используется программа ПР-6. Результаты моделирования приведены на рис. 9.

Программа ПР-6.

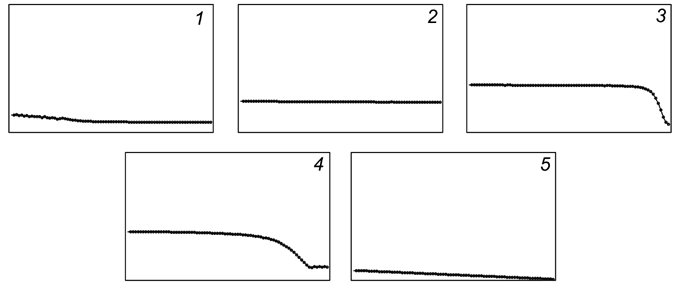
Рис. 9. Свободная поверхность жидкости в последующие моменты времени.

Рис. 9. Свободная поверхность жидкости в последующие моменты времени.

Тексты программ находятся в zip-архиве, файл gl-9.pas.

ВВЕРХ

Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net .