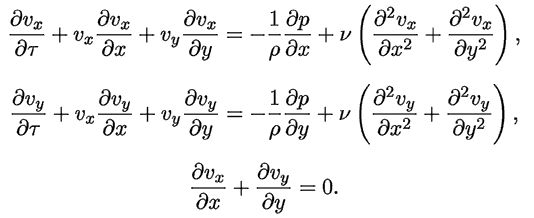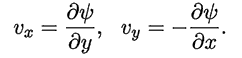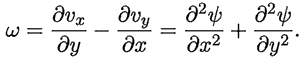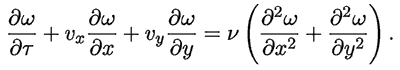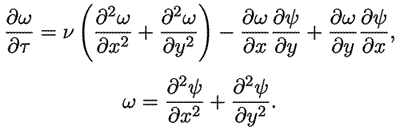Задача 1. Вязкая несжимаемая жидкость целиком заполняет двумерную прямоугольную полость, которая сверху накрыта твердой пластиной, движущейся с постоянной скоростью V (рис. 1). Стенки полости неподвижны и непроницаемы. Необходимо рассчитать поле скоростей течения жидкости.

Из уравнений Навье - Стокса для плоского течения несжимаемой вязкой жидкости следует:

Перейдем к системе уравнений Навье-Стокса в переменных “функция тока – вихрь скорости”. Введем функцию тока такую, что:

Течение двумерное, вектор завихренности перпендикулярен плоскости рисунка и равен:

Учтем, что градиент давления отсутствует. Если первое уравнение из системы Навье - Стокса продифференцировать по y, второе по x, а затем уравнения вычесть, то получится:

Последние три уравнения и составляют систему “функция тока – вихрь скорости”.

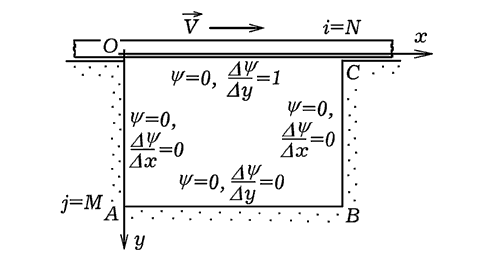
Рис. 1. Расчет течения жидкости в каверне с подвижной крышкой.

Программа ПР-1.

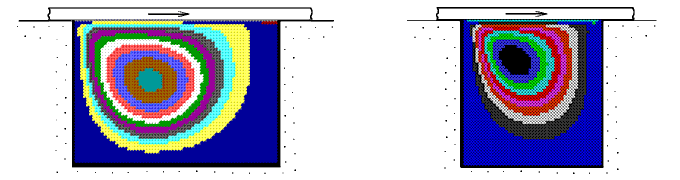
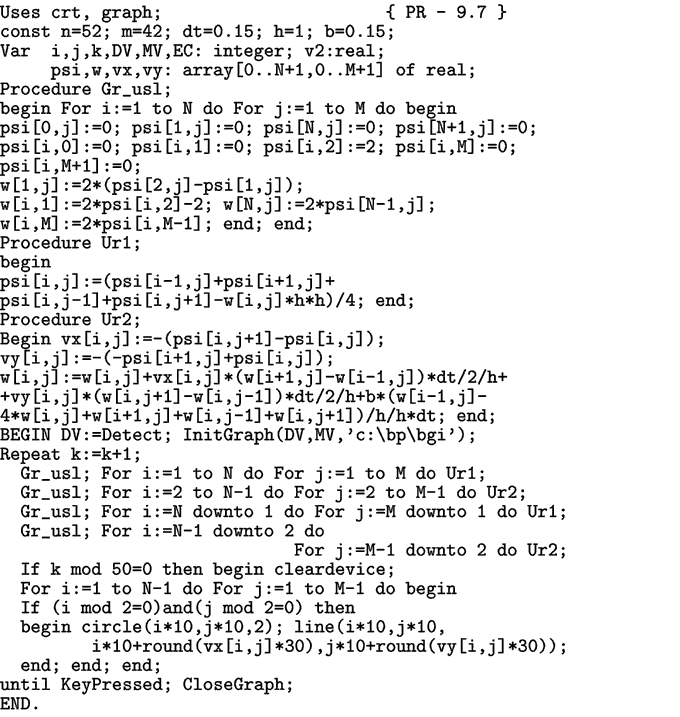
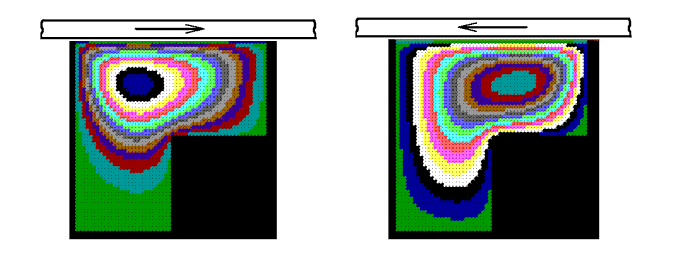
Необходимо расчетную область покрыть двумерной сеткой и записать дифференциальные уравнения в конечных разностях. Программа ПР-1 позволяет рассчитать двумерное течение вязкой несжимаемой жидкости в каверне с подвижной крышкой при различных скоростях движения крышки, вязкости жидкости, размерах каверны. Для получения решения стационарной задачи необходимо, чтобы программа выполнила более 1500 итераций. На рис. 2 и 3 показаны получающиеся распределения функции тока. Границы разноцветных областей соответствуют линиям тока. В принципе несложно построить линии тока, запустив внутрь полости частицы-маркеры.

Рис. 2. Течение жидкости в полости с движущейся крышкой

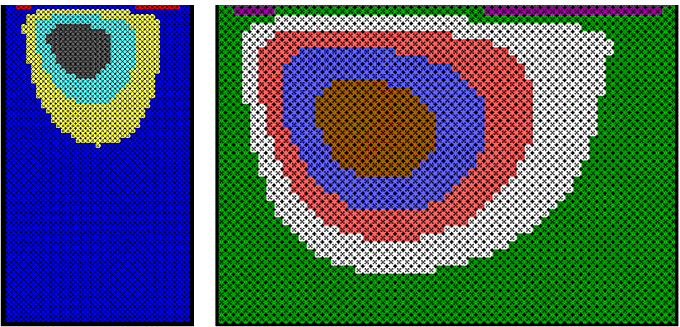
Рис. 3. Течение жидкости в полости с движущейся крышкой

Задача 2. Рассчитать двумерное течение вязкой несжимаемой жидкости в каверне с подвижными крышкой и дном в случае, когда: 1) крышка и дно движутся в одном направлении; 2) крышка и дно движутся в противоположных направлениях. В узлах двумерной сетки постройте векторы скоростей.

Внеся соответствующие изменения в предыдущую программу, можно получить программу ПР-1, которая строит на экране векторы скорости жидкости в каждом узле двумерной сетки (рис. 4 и 5).

Программа ПР-2.

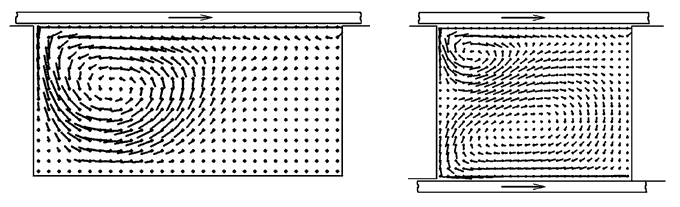
Рис. 4. Результаты расчета поля скоростей для жидкости в каверне.

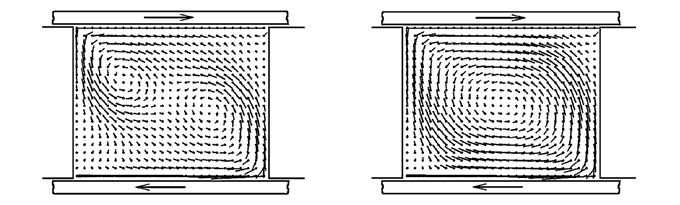
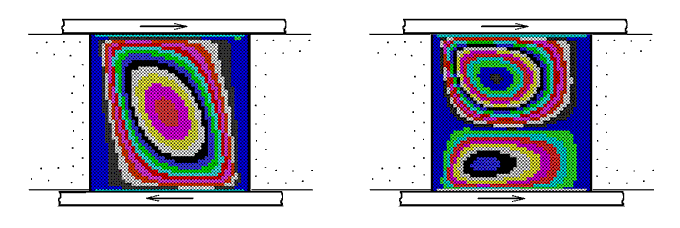
Рис. 5. Скорости дна и крышки полости противоположны.

Как видно из рис. 5 и 6, при противоположно направленных скоростях крышки и дна сначала образуются два вихря, закрученных в одном направлении, которые через некоторое время объединяются в один. Если крышка и дно движутся в одном направлении, то образуются два вихря, вращающиеся в одном направлении.

Рис. 6. Дно и крышка полости движутся.

Задача 3. Изучите движение вязкой жидкости в треугольной каверне, а также в прямоугольной каверне с уступом. Промоделируете течение, когда крышка движется: 1) влево; 2) вправо.

Результаты расчета функции тока в этих случаях представлены на рис. 7 и 8. Видно, что от формы полости и направления движения крышки сильно зависит форма образующегося завихрения.

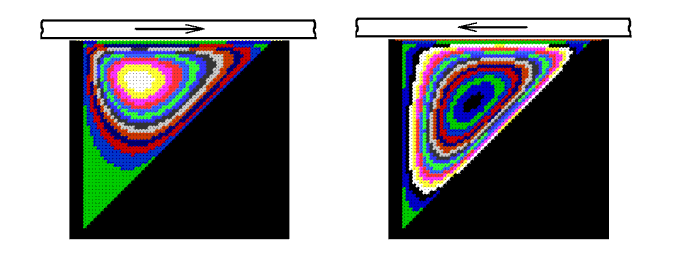
Рис. 7. Движение жидкости в треугольной полости.

Рис. 8. Движение жидкости в прямоугольной полости с уступом.

Задача 4. На преграду (пластину, каверну, уступ) набегает поток вязкой жидкости. Необходимо рассчитать поле скоростей, построить линии тока.

Рассмотрим двумерное течение вязкой несжимаемой жидкости, обтекающей преграду в декартовой системе координат XOY. Если преграда симметрична относительно направления течения, то достаточно рассчитать поле скоростей в верхней полуплоскости. Запишем систему уравнений Навье - Стокса в переменных "функция тока - вихрь скорости":

Используется программа ПР-3. Для решения задачи важно правильно задать граничные условия. В предлагаемой программе (Free Pascal) моделируется образование вихрей при обтекании вязкой жидкостью двух препятствий (рис. 9 и 10). Как заданы граничные условия, ясно из процедуры Gr_usl.

Программа ПР-3.

Рис. 9. Вихревое течение жидкости за уступом.

Рис. 10. Образование вихрей в каверне и за уступом.

Тексты программ находятся в zip-архиве, файл gl-91.pas.

Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net .