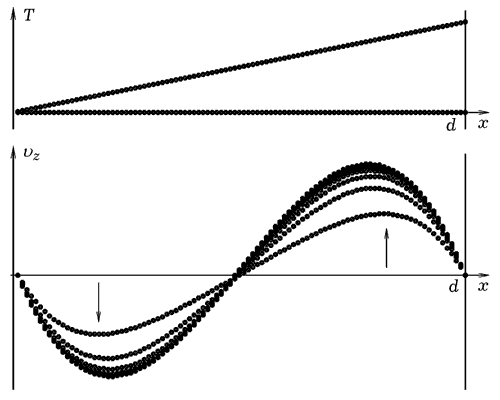
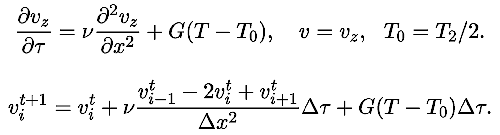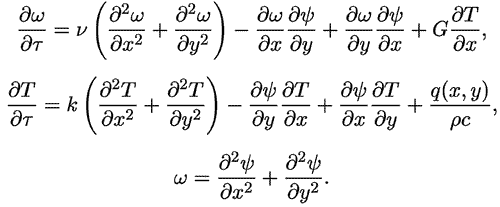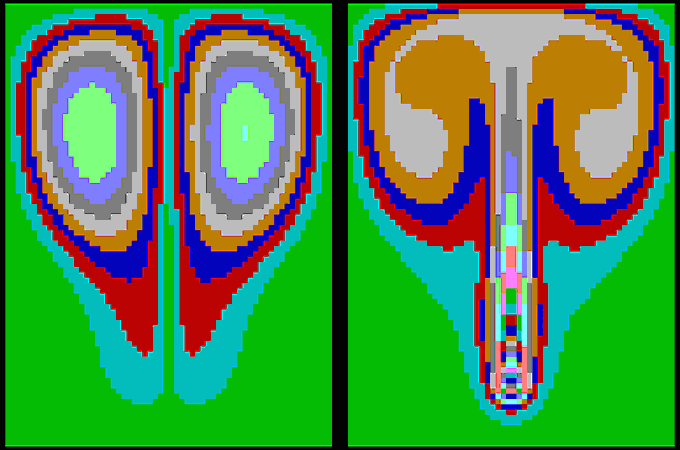Программа ПР-1, используемая для решения этой задачи, содержит цикл по времени, в котором перебираются все узлы одномерной сетки и вычисляются значения скорости vi на итерационном шаге t+1. При этом получающееся распределение скоростей релаксирует к истинному распределению (рис. 1). Программа ПР-1.
Рис. 1. Расчет течения между пластинами с разными температурами
Здесь T - температура, q - мощность источников тепла. Для численного решения этой системы уравнений строят конечно-разностную схему и задают граничные условия для функции тока, вихря скорости и температуры. Программа ПР-2, моделирующая конвективные течения вязкой жидкости в прямоугольной полости при различном распределении температуры стенок и источников тепла, представлена выше. Граничные условия заданы в процедуре Gr_usl. Они соответствуют случаю, когда дно сосуда имеет более высокую температуру и в результате конвекции возникают конвективные валы (в трехмерном случае - ячейки Бенара). Программа ПР-2.
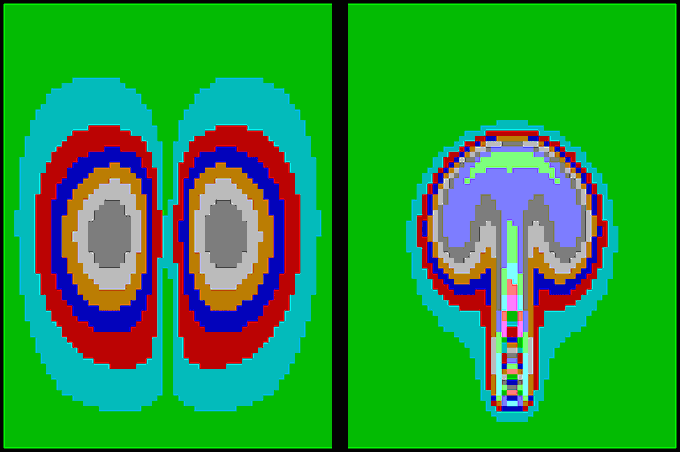
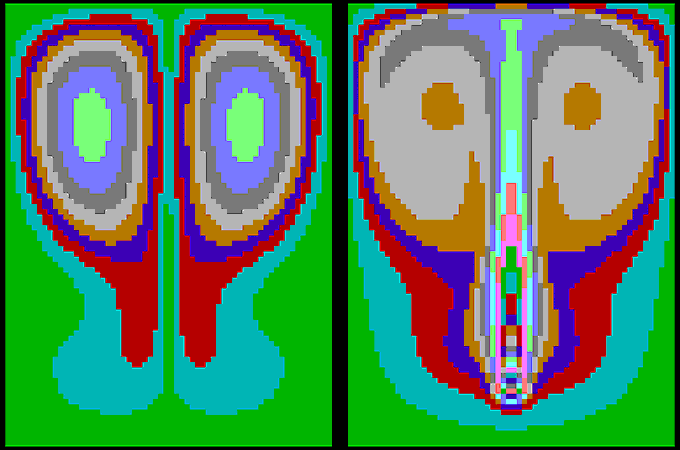
На рис. 2 и 3 сверху показано распределение функции тока (границы разноцветных областей - линии тока), а снизу - распределение температуры (границы - изотермы). Созданная компьютерная модель позволяет провести целую серию вычислительных экспериментов, изучая конвекцию при различных вязкости, теплопроводности, плотности жидкости, размерах полости, температурах ее стенок, мощностях и положениях источников тепла (холода). Например, на рис. 8 показан результат расчета поля скоростей (слева) и поля температур (справа) в случае, когда нагревается левая стенка полости. Хорошо видно, что возникает вихревое движение жидкости, более нагретые слои поднимаются по левой стенке вверх, затем вправо и опускаются. При запуске программы на экране монитора возникают цветные динамические анимации, формирующие наглядный образ изучаемых явлений.
Рис. 2. Поля скоростей и температур при конвекции (подогрев снизу).
Рис. 3. Моделирование конвекции и образования валов (ячеек Бенара)
Рис. 4. Результаты моделирования конвекции (подогрев сбоку).
Рис. 5. Поле скоростей и поле температур при конвективном течении
Необходимо задать граничные условия соответствующим образом. Результат моделирования представлен на рис. 6.
Рис. 6. Конвекция при разности температур между боковыми стенками
Рис. 8. Точечный источник тепла расположен на оси симметрии
Рис. 9. Точечный источник тепла смещен влево Тексты программ находятся в zip-архиве, файл gl-92.pas. ВВЕРХ
Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net . |