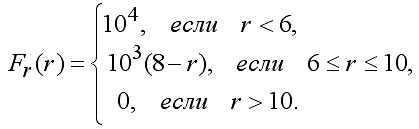НАЗАД
Развитием метода молекулярной динамики стал метод частиц, который заключается в представлении тела совокупностью крупных шарообразных частиц, взаимодействующих и движущихся в соответствии с законами классической механики. При удалении частицы притягиваются, а при сближении отталкиваются. Движение каждой частицы может быть рассчитано из второго закона Ньютона. Иногда используют частицы-маркеры, позволяющие визуализировать движение различных слоев жидкости или газа.
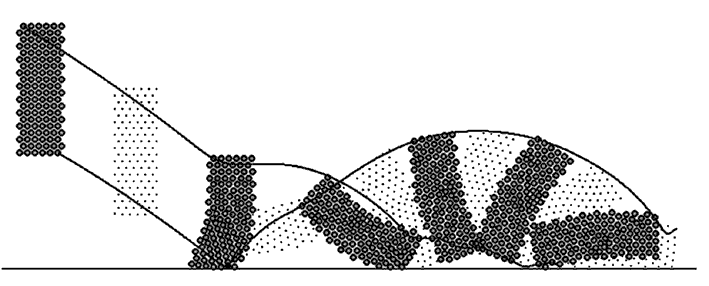
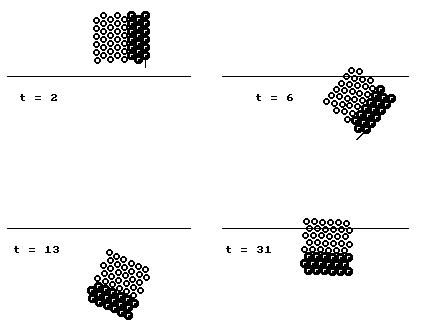
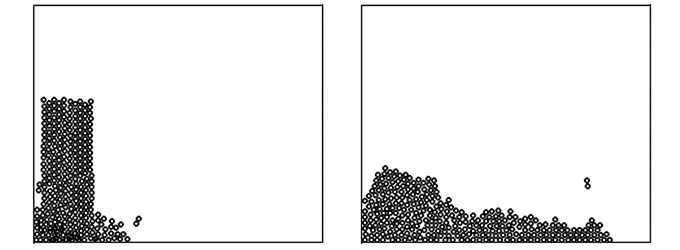
При неупругих деформациях когда i-тая частица смещается относительно соседней j-той частицы, на i-тую частицу действует сила вязкого трения. Она направлена в сторону противоположную относительному движению. Чтобы ее расчитать на каждом временном шаге t формируется матрица S, элементами которой являются расстояния s[i,j] между i-ой и j-ой частицами в момент t-1. Тогда сила внутреннего трения будет равна -r*(l-s[i,j])/dt, где l - расстояние между i-ой и j-ой частицами в момент t, а выражение в скобках пропорционально скорости относительного движения этих частиц. В программе последовательно перебираются все частицы и для каждой определяется равнодействующая всех действующих сил (включая силу тяжести). После этого вычисляется ускорение, скорость и координаты каждой частицы в следующий момент t+1. Используется программа ПР-1, результаты моделирования представлены на рис. 1. Программа ПР-1.
Рис. 1. Падение неупругого тела на горизонтальную поверхность.
При моделировании взаимодействия частицы с первоначально покоящимся кубом получаются результаты, представленные на рис. 2.1. В соответствии с законами сохранения импульса и момента импульса, центр масс куба начнет двигаться вправо, а сам куб -- вращаться. Когда движущаяся частица соударяется с одной из вершин куба, в общем случае происходит нецентральный удар; частица и куб разлетаются (рис. 2.2). На рисунках также показаны траектории движения двух максимально удаленных точек тела. Куб сохраняет свою форму, потому что изменены коэффициенты в выражении для силы взаимодействия частиц.
Рис. 2. Частица отлетает от одной из вершин куба. Частица сталкивается с кубом; куб отскакивает от поверхности. Для того, чтобы промоделировать неупругое столкновение частицы с телом кубической формы, необходимо предусмотреть возникновение силы притяжения между одиночной частицей и частицами куба. После абсолютно неупругого удара частица и куб движутся как единое целое, вращаясь вокруг общего центра масс (в общем случае).
Программа ПР-2.
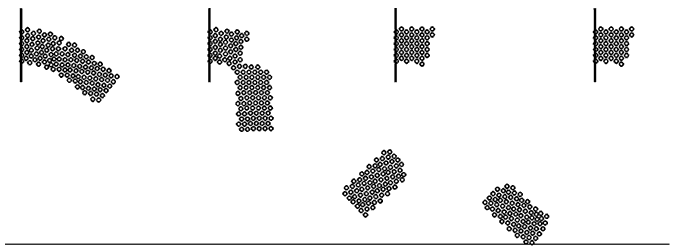
Рис. 3. Моделирование разрушения балки.
Программа ПР-3.
Рис. 4. Движение тела, упавшего на поверхность жидкости.
Программа ПР-4.
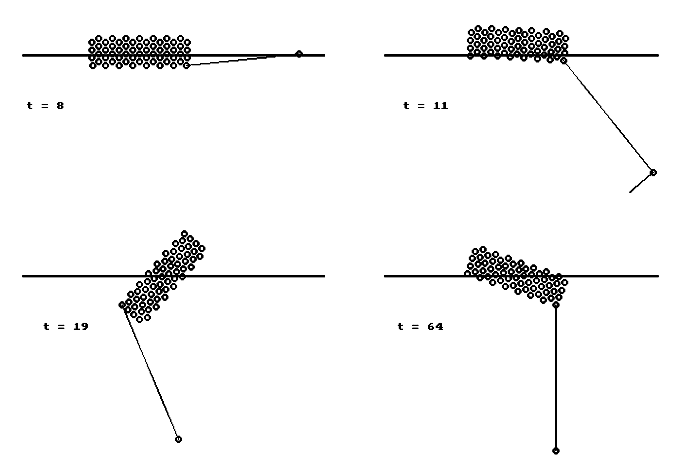
Рис. 5. Движение плавающего бревна и привязанного к нему груза.
Программа ПР-5.
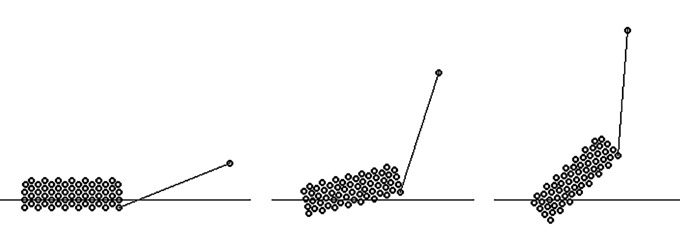
Рис. 6. Движение плавающего бревна, которое тянут за нить.
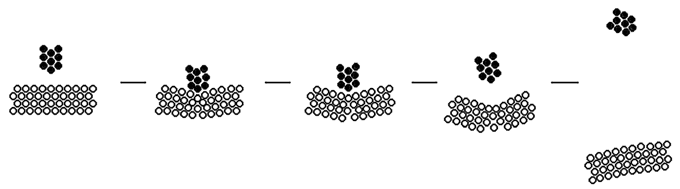
Чтобы построить двумерную модель взаимодействия снаряда и мишени незначительно модифицируем программу ПР-6. Результат моделирования частично упругого удара при достаточно большой массе мишени представлен на рис. 7. Видно, что сразу после удара мишень деформируется и "отталкивает" снаряд. В программе исключены силы притяжения, действующие между частицами снаряда и мишени. Программа ПР-6.
Рис. 7. Частично неупругое соударение снаряда и мишени. Если уменьшить коэффициенты упругости и вязкости, а также сделать так, чтобы модель учитывала силы притяжения, возникающие при сближении частиц снаряда и мишени, то удастся промоделировать абсолютно неупругий удар (рис. 8). После взаимодействия деформированные снаряд и мишень движутся с равными скорстями и вращаются, что соответствует законам сохранения импульса и момента импульса.
Рис. 8. Абсолютно неупругое соударение снаряда и мишени.
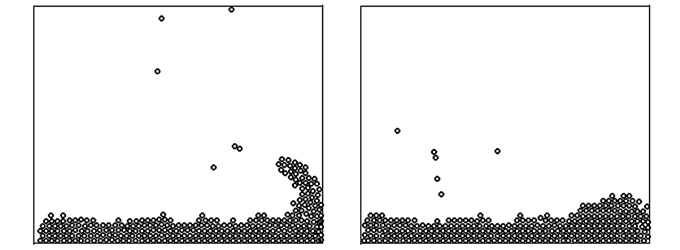
Задача решается аналогично, необходимо только иначе задать силу взаимодействия между частицами F(r): Если r больше 10, то F=0; (частицы не взаимодействуют) Если r лежит в интервале [7; 10], то F=-1000; (частицы притягиваются) Если r меньше 7, то F=20000; (частицы отталкиваются).Кроме того, следует задать условие отражения молекул от границ сосуда и начальное состояние системы. При запуске программы ПР-7 моделируется обрушение столба жидкости, которая движется по дну сосуда к его правой стенке, соударяется с ней, а потом движется обратно (рис. 9). Модель также позволяет изучить поведение системы в случае, когда жидкость имеет высокую вязкость и медленно растекается по дну сосуда. Программа ПР-7.
Рис. 9. Обрушение столба жидкости.
Используется предыдущая программа ПР-7. Чтобы заставить "перемещаться" левую стенку сосуда, следует задать условный оператор: если x[i] меньше 160+30*tt, то Fx[i]:=5E+4. Получающийся результат представлен на рис. 10. Видно, что сначала у левой стенки образуется подъем, средняя часть жидкости начинает двигаться вправо и упирается в правую стенку сосуда. У правой стенки сосуда частицы жидкости начинают двигаться вверх и влево. Средний уровень поверхности жидкости в сосуде повышается. Внеся незначительные изменения в программу ПР-7, можно добиться того, что на экране через равные промежутки времени вместо частиц будут появляться отрезки, сонаправленные с векторами скорости (то есть поле скоростей).
Рис. 10. Сгребание жидкости, лежащей на дне сосуда.
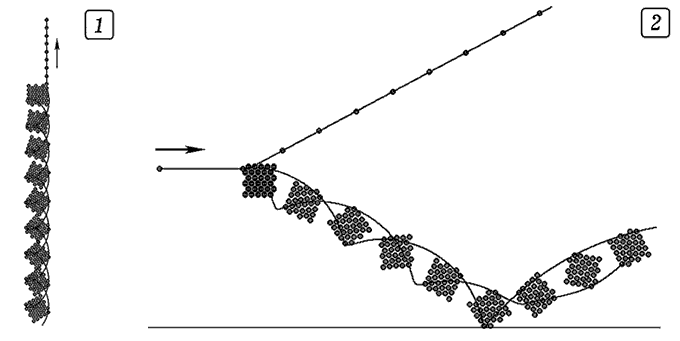
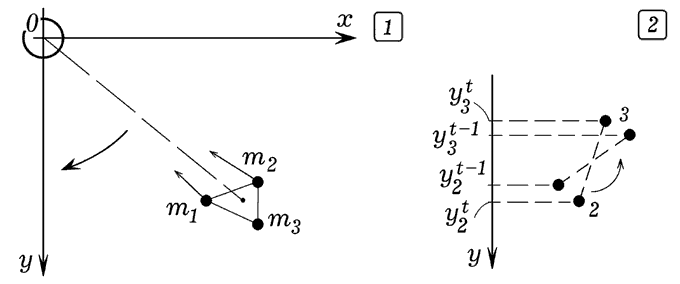
Рис. 11. Моделирование вращения вязкого спутника. Метод решения этой задачи рассмотрен в книге Woolfson M.M., Pert G.J. An Introduction to Computer Simulation (Oxford University Press, 1999. –– 311 p.) на страницах 17-22. Он состоит в рассмотрении движения и взаимодействия трех частиц, моделирующих спутник, связанных упругими силами, и движущимися вокруг планеты расположенной в начале координат O (рис. 11). Со стороны планеты на каждую из трех частиц действует сила гравитационного притяжения. Частицы притягиваются друг к другу, а при сближении взаимодействуют друг с другом с силами упругости. При относительном движении между частицами действует сила вязкого трения. Программа ПР-8.
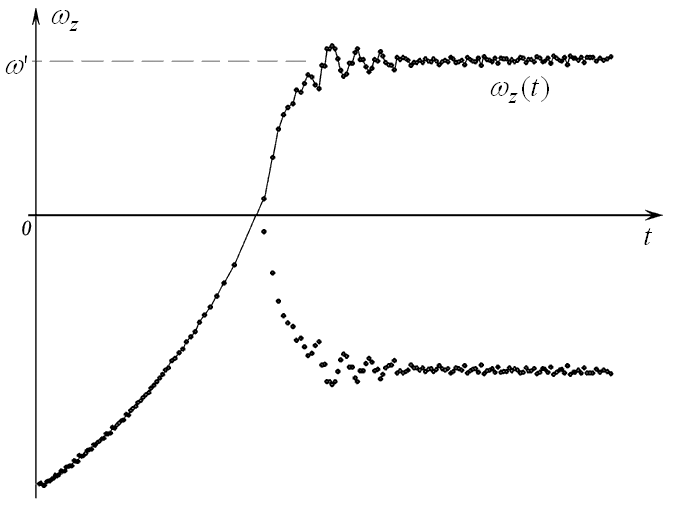
Используется программа ПР-8. Она позволяет рассчитать положение планеты и трех частиц, моделирующих спутник, а также строит график зависимости угловой скорости вращения спутника от времени. Начальные условия заданы так, что спутник вращается вокруг планеты по часовой стрелке, а вокруг своей оси -- в противоположном направлении, то есть против часовой стрелки. В результате движения в неоднородном поле планеты образующаяся приливная волна (обусловденная деформацией спутника и действием сил вязкого трения) уменьшает скорость вращения спутника вокруг своей оси, а затем заставляет его вращаться в направлении орбитального движения. На экране получается график зависимости модуля угловой скорости вращения спутника от времени (рис. 12). Видно, что угловая скорость спутника стремится меняет знак и затем стремится к некоторой постоянной величине ω'. Ее значение совершает затухающие колебания относительно ω'. Следует понимать, что в нашем случае спутник движется не по эллиптической орбите с небольшим эксцентриситетом (как Луна вокруг Земли), а по сильно вытянутой незамкнутой орбите. При этом он близко приближается к планете (в область с сильно неоднородным гравитационным полем); в этот момент приливная волна оказывает наибольшее влияние на торможение спутника и его раскручивание в обратном направлении.
Рис. 12. Зависимость скорости вращения спутника от времени. Тексты программ находятся в zip-архиве, файл gl1-10.pas. ВВЕРХ
Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net . |