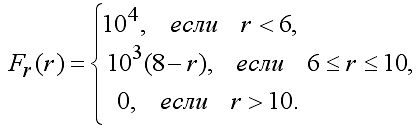НАЗАД
Здесь расстояние между частицами r и сила взаимодействия F заданы в условных единицах. Для нахождения силы вязкого трения определяют скорость смещения i-той частицы относительно каждой частицы, находящейся в ее окрестности, и вычисляют проекции r(l-s1[i,j])cosα/dt и r(l-s1[i,j])sinα/dt. Здесь α -- угол между прямой, соединяющей i-ую и j-ую частицы, и горизонтальной осью Ox. Тогда cosα=(xi-xj)/l, sinα=(yi-yj)/l. В самом начале работы программа создает массив s[i,j], в котором сохраняются расстояния между частицами тела при отсутствии деформаций. Содержимое этого массива не изменяется. Состояние системы в последующие моменты времени рассчитываются в цикле по t Repeat ... until. На каждом временном шаге определяются проекции ускорения ax, ay, скорости vx, vy и координаты x, y всех частиц тела, а также определяются расстояния между ними, которые сохраняются в массиве s1[i,j]. Зная расстояния между i-той и j-той частицами в недеформированном и деформированном состояниях можно найти проекции силы упругости. Определив скорость из относительного смещения частиц, можно вычислить проекции силы вязкого трения.
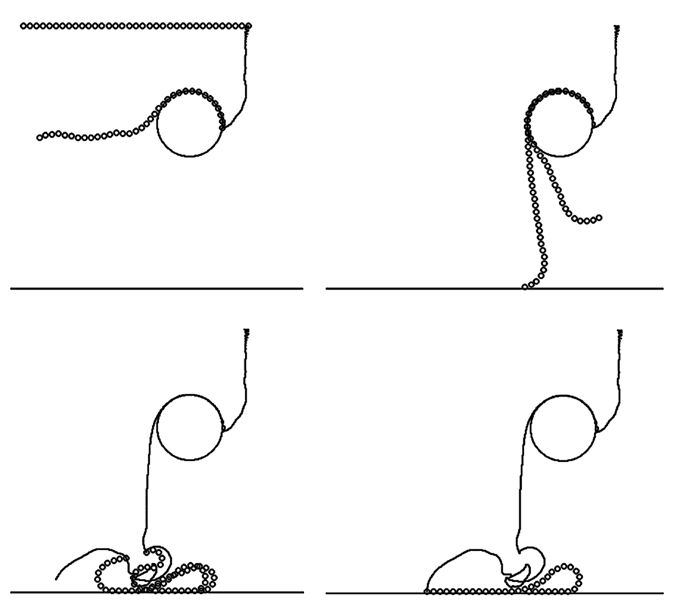
Рис. 1. Силы, действующие на частицы тела. При соударении линейки с горизонтально расположенным цилиндром на i-тую частицу, соприкасающуюся с цилиндром, действует сила F (рис. 1.2). В программе рассчитываются синус и косинус угла α между прямой, идущей от центра цилиндра к этой i-той частице, и горизонтальной осью Ox: cosα=(x0-xi)/r, sinα=(y0-yi)/r. Здесь r -- радиус цилиндра. Если i-тая частица приблизилась к точке O' на расстояние меньшее r, то программа "отодвигает" частицу на расстояние чуть большее r и уменьшает ее проекции скорости. Программа ПР-1.
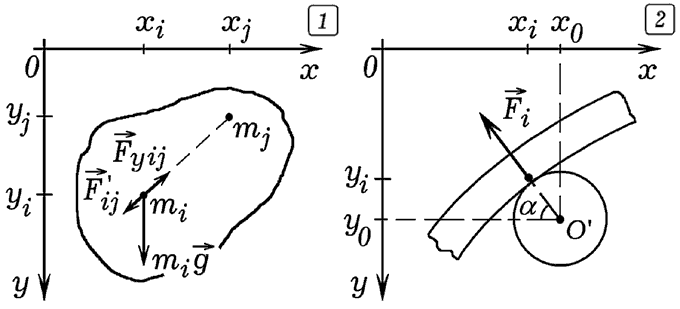
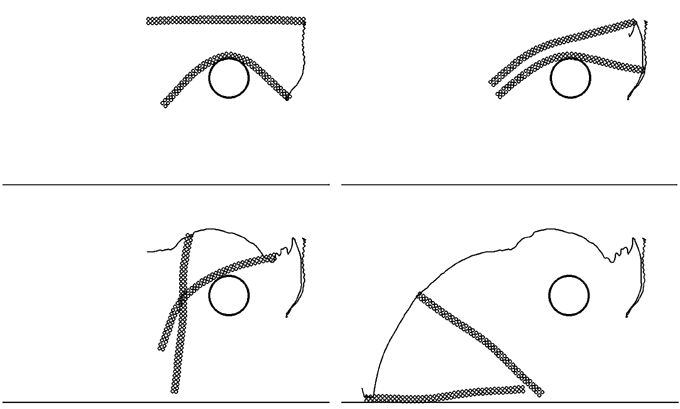
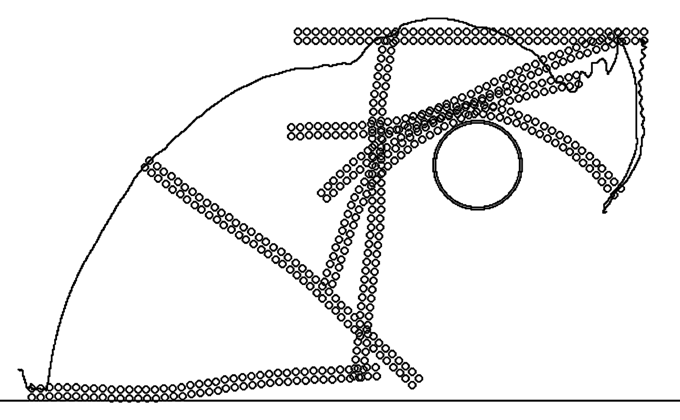
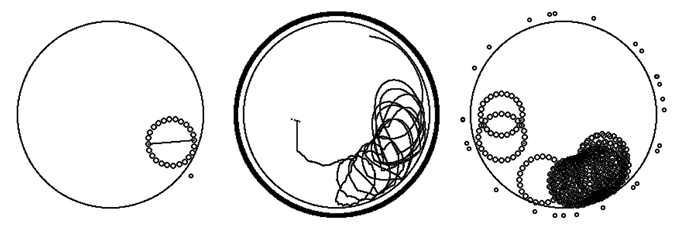
Используется программа ПР-1. Результаты моделирования движения вязкоупругого стержня при падении на цилиндр, а затем на горизонтальную плоскость представлены на рис. 1 и 2. На них показаны положения стержня в различные моменты времени и траектория одной из точек тела. Сначала стержень движется практически поступательно, после удара о цилиндр стержень подпрыгивает и совершает свободные колебания, изгибаясь в ту и другую стороны. Под действием силы тяжести центр масс стержня стремится занять самое низкое положение. Стержень переворачивается, соударяется с горизонтальной плоскостью, по нему бежит изгибная волна. Через некоторое время за счет действия сил вязкого трения система переходит в состояние покоя.
Рис. 2. Падение неупругого тела на цилиндр и поверхность.
Рис. 3. Падение неупругого стержня на цилиндр и поверхность.
В предыдщей задаче стержень моделировался двумя рядами частиц, между которыми действовали вязкоупругие силы. Чтобы промоделировать нить достаточно рассмотреть один ряд частиц. Во всем остальном задача решается совершенно аналогично. Программа ПР-2.
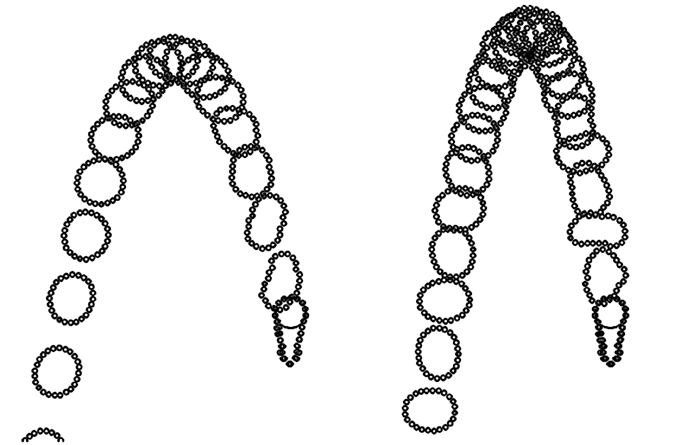
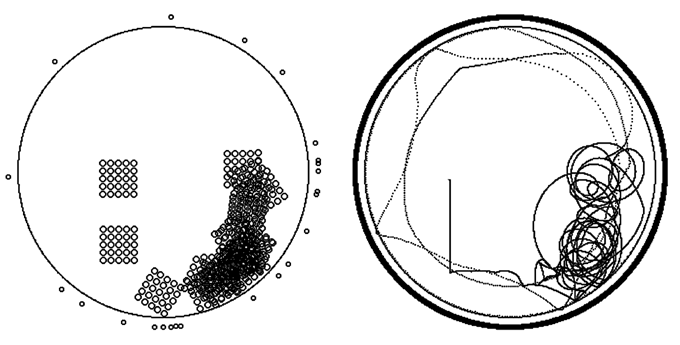
Используется программа ПР-2. На рис. 4 показано положение нити в различные моменты времени, а также траетория движения частицы с номером i=N. Видно, как нить охватывает цилиндр, затем соскальзывает с него на горизонтальную поверхность.
Рис. 4. Падение нити на горизонтальный цилиндр, а затем на поверхность.
Программа ПР-3.
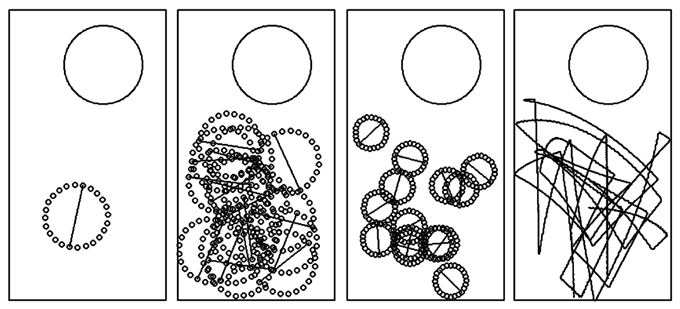
Рис. 5. Движение резинового кольца.
Программа ПР-4.
Используется программа ПР-4. На рис. 6 приведены типичные результаты моделирования, показаны положения шарика в различные моменты времени, а также траектория движения одной из его частиц. Видно, система находится в состоянии, которое называется динамический хаос.
Рис. 6. Движение шарика в сосуде с колеблющимся дном.
Используется метод больших частиц, вместо кольца будем рассматривать совокупность частиц, связанных между собой вязкоупругими силами. Задача решается тем же методом, что и предыдущие. Используется программа ПР-5, результаты моделирования -- на рис. 7. Программа ПР-5.
Рис. 7. Движение кольца (цилиндра) внутри вращающейся трубы.
Программа ПР-6.
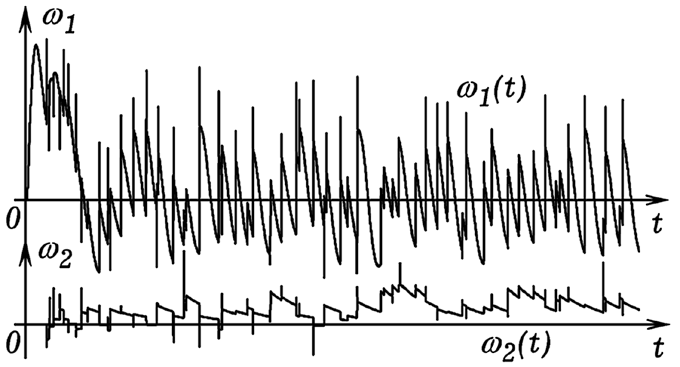
Рис. 8. Движение куба внутри вращающейся трубы. Получающиеся графики представлены на рис. 9. Видно, что угловая скорость w1 совершает затухающие колебания относительно нулевого значения. Это объясняется тем, что изначально система находилась не в положении равновесия (кубик падал на внутреннюю поверхность вращающейся трубы левее вертикального осевого сечения). Так как кубик чаще вращается против часовой стрелки, то w2 как правило положительна. Вертикальные участки графиков соответствуют моментам, когда кубик не скользит относительно трубы, а движется вместе с ней. В случае, когда кубик отрывается от внутренней поверхности трубы, его центр масс медленно движется вверх, затем вниз, а сам кубик вращается вокруг него с медленно уменьшающейся скоростью.
Рис. 9. Графики зависимостей угловых скоростей w1z и w2z от времени. Тексты программ находятся в zip-архиве, файл gl1-11.pas. ВВЕРХ
Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net . |