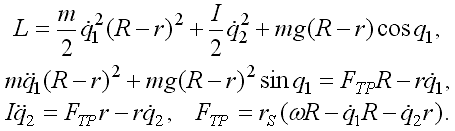НАЗАД
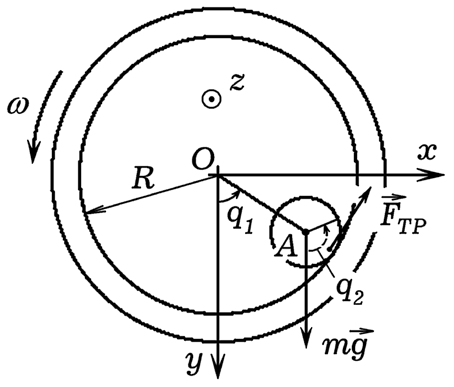
Рис. 1. Расчет качения цилиндра во вращающейся трубе. Система имеет две степени свободы. Введем две обобщенные координаты q1 и q2 (в рад). Запишем функцию Лагранжа и систему из двух уравнений Лагранжа:
При этом учитывается, что сила вязкого трения между поверхностями трубы и цилиндра пропорциональна скорости движения точек одной поверхности относительно другой. Тормозящий момент, действующий в подшипниках пропорционален угловой скорости вращения. Программа ПР-1.
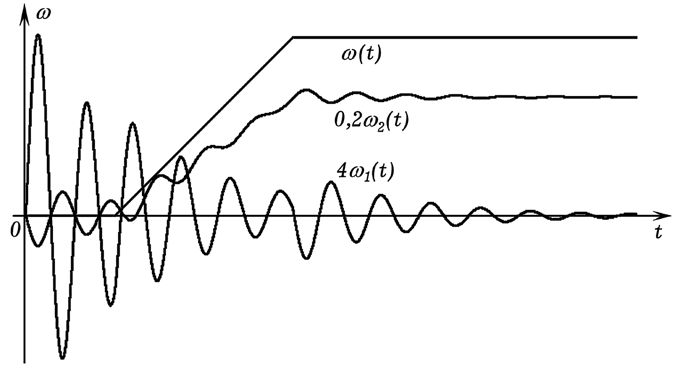
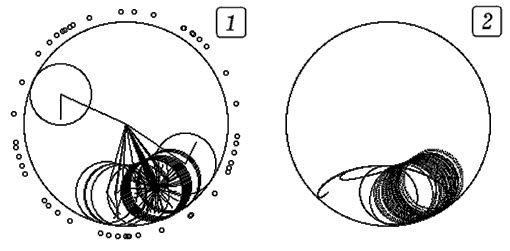
Используется программа ПР-1, результаты моделирования движения цилиндра представлены на рис. 2 и 3. Допустим, что в начальный момент система находилась в состоянии q1=-1, q2=0 и w1z и w2z=0, причем труба была неподвижна. Систему предоставляют самой себе и через некоторое время t1 скорость вращения трубы w начинает расти пропорционально времени, а затем, достигнув некоторого значения w', остается постоянной. Из графиков, изображенных на рис. 2, понятно, как изменяются проекции угловой скорости движения кривошипа ОА w1z и скорость вращения цилиндра w2z с течением времени. Так как система выведена из положения равновесия, то кривошип (а значит и w1z) сначала совершает затухающие колебания; после разгона трубы он продолжает колебаться относительно положения, смещенного от положения равновесия. Угловая скорость цилиндра сначала также совершает затухающие колебания, а после разгона трубы увеличивается стремясь к некоторому положительному значению. При этом цилиндр находится в правом нижнем положении и вращается против часовой стрелки (рис. 2.1). На рис. 2.2 изображена траектория движения одной из точек на боковой цилиндра.
Рис. 2. Расчет качения цилиндра во вращающейся трубе.
Рис. 3. Расчет качения цилиндра во вращающейся трубе. Тексты программ находятся в zip-архиве, файл gl1-11.pas. ВВЕРХ
Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net . |