Задача 1. Имеется Общество, в котором люди могут дожить до 80 лет. Люди в возрасте от 0 до 20 лет учатся за за счет Общества, а в возрасте от 20 до 60 лет работают, увеличивая размеры Госбюджета. Люди в возрасте от 20 до 40 лет способны родить ребенка, причем эта способность пропорциональна уровню жизни. За счет болезней люди всех возрастов умирают. Часть Госбюджета идет на социальные нужды: пособие за рождение ребенка, обучение людей до 20 лет. Создайте имитационную модель общества, которое существует стабильно. Получите распределение численности L людей по возрастам v=1, 2,..., 80.

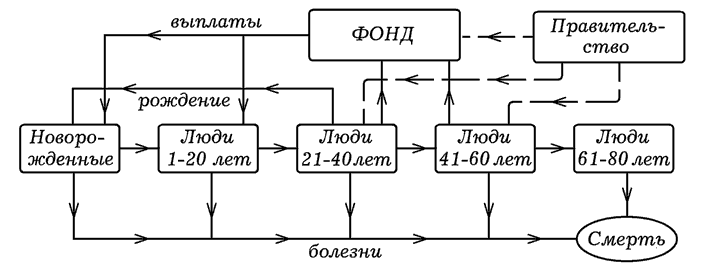
Рис. 1. Кибернетическая модель Общества.

Для решения задачи будем использовать кибернетический подход (рис.1). Все население разобьем на несколько категорий: новорожденные (их родители получают выплаты за рождение), люди в возрасте 1-20 лет (учатся за счет государства), люди в возрасте 21-40 лет (работают, платят налоги), люди в возрасте 41-60 лет (работают, платят налоги), люди в возрасте 61-80 лет (получают пенсию). Пусть время t изменяется с шагом 1 год. Число людей в возрасте m лет обозначим через Lm, а число людей возраст которых лежит в интервале от n до m лет включительно -- через Ln-m. Количество денег в Госбюджете B(t+1) в t+1 году равно:

B(t+1)=B(t)+p₁L_20-60(t) -p₂L₀(t)- p₃L_0-20(t),

где B(t) -- объем Госбюджета в t-ом году, p₁ -- прирост Госбюджета, приносимый одним человеком в возрасте от 20 до 60 лет за 1 год (налоги), p₂ -- объем однократного пособия за рождение ребенка, p₃ -- средняя стоимость одного года обучения человека в возрасте от 0 до 20 лет. Через L₀(t) обозначим число родившихся в t-ом году детей. Часть всех имеющихся у государства денег идет на социальные выплаты S(t)=k₁B(t), которые равномерно распределяются между всеми членами Общества, и каждый получает S(t)/L_0-80(t). Этой величине пропорционален уровень жизни U(t), находящийся в интервале от 0 до 1. Можно записать:

U(t)=k₂ S(t)/L(t)_0-80.

Количество родившихся в (t+1)-ом году детей прямо пропорционально количеству людей репродуктивного возраста от 20 до 40 лет L_20-40(t+1) и уровню жизни U(t+1). Можно записать:

L₀(t+1)= αL_20-40(t)(U(t+1)+k₃).

За счет болезней люди умирают, их количество сокращается: L(t+1)=L_i(t)(1-b), где b -- коэффициент смертности, который зависит от возраста.

Алгоритм АЛ-1.

Программа ПР-1, моделирующая Общество, реализует алгоритм АЛ-1. Она содержит цикл по t, в котором пересчитываются все характеристики системы с шагом 1 год и результаты выводятся на экран. Понятно, что рассматриваемая модель очень грубая и не учитывает многих факторов и представляет интерес только для учебных целей. Параметры подобраны так, чтобы после запуска система, совершив несколько колебаний, оказалась бы в состоянии динамического равновесия, число людей в государстве оставалось бы практически постоянным.

Программа ПР-1.

При случайном задании параметров компьютерная модель ведет себя нестабильно: численность населения либо начинает резко возрастать, либо уменьшается до нуля. Даже при удачном подборе параметров не получится подобрать правильное распределение числа людей по возрастам, при котором Общество сразу существовало бы стабильно (без скачков и провалов численности населения). В этом случае после запуска программы система совершает затухающие колебания и переходит в устойчивое состояние.

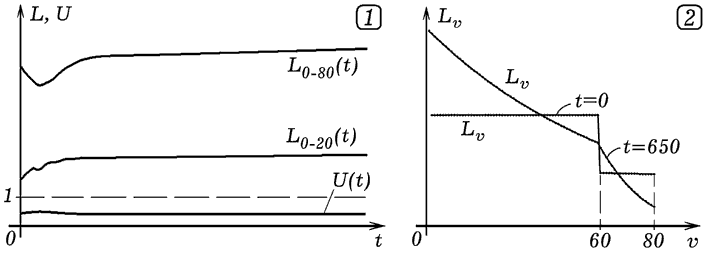
Рис. 2. Переход модели Общества в устойчивое состояние.

В нашей модели исходное распределение численности по возрастам задано так: до 60 лет L_v(0)=100, а после 60 L_v(0)=50; ему соответствует кривая L_v(0) на рис. 2.2. Это достаточно произвольное задание начального состояния системы. После запуска программы модель стремится перейти к правильному распределению численности населения по возрастам, соответствующему заданным параметрам. На рис. 2.2 ему соответствует график L_v(650) в момент t=650 лет. После этого ни численность населения, ни ее распределение по возрастам существенно не изменяются. Если начальное распределение численности людей по возрастам задать иначе, то система все равно через некоторое время будет стремиться к состоянию динамического равновесия, соответсвующему распределению L_v(650).

Задача 2. Создайте компьютерную модель Общества, которое существует стабильно. Изучите зависимость численности населения от времени в случаях, когда доля выплат из Госбюджета в Социальный фонд: а) увеличивается; б) уменьшается.

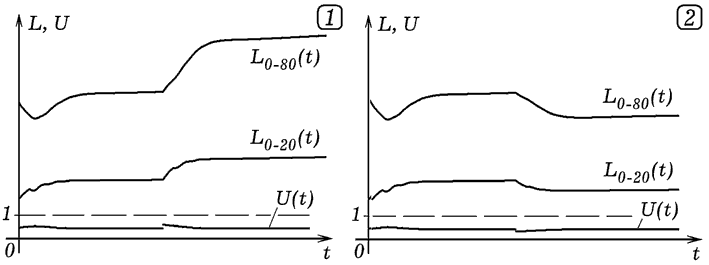
Допустим, с 300 года Правительство решает увеличить объем социального фонда и повышает k от 0,25 до 0,35: If god>300 then k:=0.35;. Реакция системы видна из рис. 3: уровень жизни и численность населения увеличиваются, затем уровень жизни возвращается к первоначальному значению, численность населения стабилизируется на каком-то более высоком уровне. Это обусловлено тем, что рождение большего количества детей приводят к увеличению затрат на пособия и их обучение.

При уменьшении доли k от 0,25 до 0,20 уровень жизни уменьшается, что приводит к снижению рождаемости. Уменьшение неработающих членов Общества приводит к возврату уровня жизни на прежний уровень и стабилизации рождаемости и численности населения на более низком уровне.

Рис. 3. Реакция модели Общества на изменение размера соцфонда.

Задача 3. Допустим Общество находилась в состоянии динамического равновесия и в момент t случился кризис, в результате которого количество денег в Госбюджете резко уменьшилось (допустим, они были вывезены из страны). Необходимо промоделировать Общества до и после кризиса.

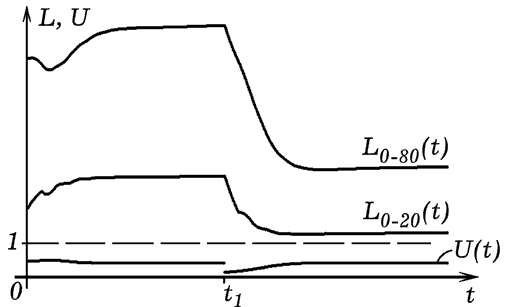
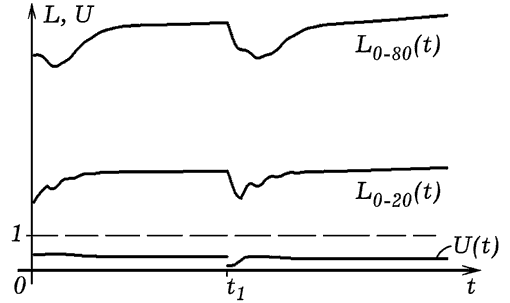
При запуске программы ПР-1 сначала происходит переходный процесс: модель входит в состояние динамического равновесия (левая часть графика на рис. 4). После этого моделируемое Общество развивается стабильно, численность населения изменяется очень медленно. Предположим, что в некоторый момент t=300 лет происходит экономический кризис, количество денег в Госбюджете уменьшается в 3 раза. Чтобы промоделировать эту ситуацию, необходимо активизировать оператор:

Результат работы программы представлен на рис. 4. Хорошо видно, что при уменьшении количества денег в бюджете государства наступает демографический кризис: резко падает уровень жизни и как следствие уменьшается рождаемость и численность населения. Снижение уровня жизни граждан приводит к падению рождаемости. Численность населения уменьшается, затем ситуация снова стабилизируется, но численность населения не восстанавливается. Это объясняется тем, что в результате кризиса в Обществе родилось меньше людей, способных в будущем дать новое поколение.

Рис. 4. Моделирование кризиса при резком уменьшении Госбюджете.

Задача 4. Допустим Общество находилась в состоянии динамического равновесия и в момент t случился кризис, в результате которого количество денег в Госюджете резко уменьшилось в 3 раза. С помощью имитационной модели найдите выход из демографического кризиса. Что должно сделать Правительство, чтобы вернуть численность населения на прежний уровень?

Представим себе, что Правительство с некоторым запаздыванием реагирует на ухудшение экономической ситуации и с 310 по 330 году плавно повышает долю социальных выплат, изменяя коэффициент k₁ c 0,25 до 0,6 со скоростью на 0,02 в год. Теперь представим себе, что Правительство, используя средства массовой информации, сумело заинтересовать молодых людей в рождении большего количества детей, и в период 310--330 повысило коэффициент рождаемости α с 0,1 до 0,11. Необходимо раскомментировать соответствующий оператор.

Из рис. 5 видно, что имеет место "демографическая яма" : численность населения сразу после кризиса падает, затем, после соответствующих действий правительства через 100 лет возвращается к исходному уровню. Колебания численности населения в возрасте 0-20 лет имеют периодичность, сравнимую с длительностью поколения. Они объясняются тем, что поколение с большим числом людей через 20-30 лет воспроизводит новое поколение с большим числом людей.

Рис. 5. Выход из демографического кризиса.

Рассмотренная модель не учитывает большое количество факторов и достаточно приближенно отражает процессы происходящие в реальном Обществе. Тем не менее она позволяет понять основную идею использования имитационных моделей для понимания некоторых социальных и экономических процессов.

Тексты программ находятся в zip-архиве, файл gl2-11.pas.

Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net .