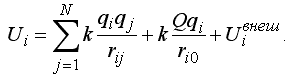РАСПРЕДЕЛЕНИЕ ЗАРЯДОВ В ПРОВОДНИКЕ
Задача 1.

Проводник помещают во внешнее электрическое поле. Необходимо промоделировать распределение электронов, если: 1) поле создано точечным зарядом; 2) поле однородное.

При внесении проводника во внешнее электростатическое поле происходит электростатическая индукция. При этом электроны в проводнике перераспределяются так, что суммарная потенциальная энергия U их взаимодействия друг с другом и внешним полем становится минимальной. Используемая программа ПР-1 содержит цикл, в котором случайным образом изменяются координаты xi и yi каждого заряда и вычисляется потенциальная энергия его взаимодействия с другими зарядами по формуле:

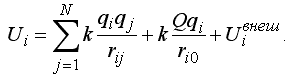
Если полученное новое значение потенциальной энергии Ui оказывается меньше старого, то это изменение координат принимается, а в противном случает -- отвергается. Затем все повторяется снова.

Программа ПР-1.

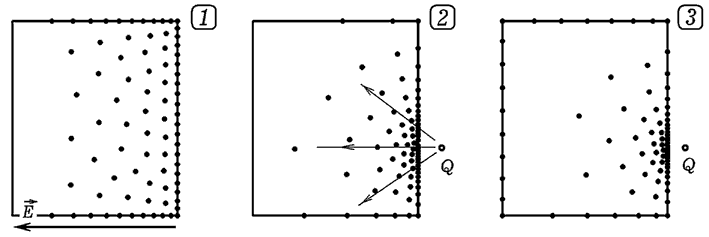
Рис. 1. Распределение электронов в проводнике во внешнем поле.

Рис. 1. Распределение электронов в проводнике во внешнем поле.

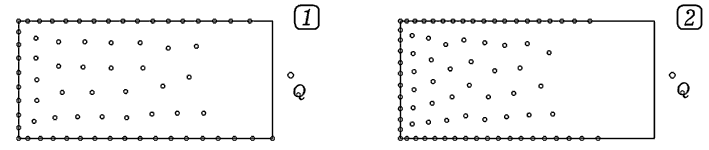
Рис. 2. Распределение электронов в поле отрицательного заряда.

Рис. 2. Распределение электронов в поле отрицательного заряда.

Результаты вычислений представлены на рис. 1 и 2. Видно, что в случае положительного заряда Q минимуму потенциальной энергии соответствует расположение электронов, при котором они приближаются к заряду Q. В случае отрицательного заряда Q электроны стараются максимально удалиться от него. Так как электроны отталкиваются друг от друга, то часть из них располагаются на поверхности проводника.

Задача 2.

К прямоугольному проводящему заряженному телу приблизили заряженный шар. Необходимо промоделировать распределение свободных электронов, если тело и шар имеют: 1) заряды одного знака; 2) заряды противоположных знаков.

Задача решается аналогичным образом. Все частицы разделяются на две группы: 1) принадлежащие телу 1 и имеющие заряд q1; 2) принадлежащие телу 2 и имеющие заряд q2. Используется программа ПР-2, в которой вычисляется суммарная потенциальная энергия взаимодействия U всех зарядов и ищется такое их распределение, при котором U минимально. На рис. 3 представлены результаты моделирования для случаев: 1) заряды одноименные (рис. 3.1); 2) заряды разноименные (рис. 3.2).

Программа ПР-2.

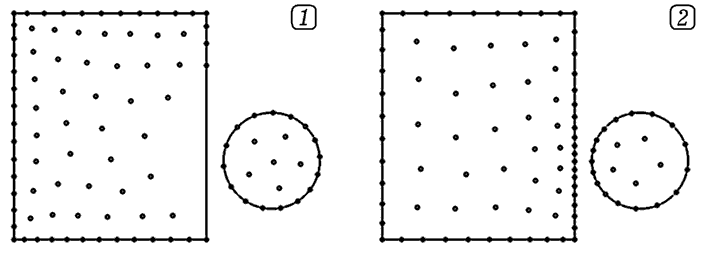
Рис. 3. Распределение электронов в проводящих заряженных телах.

Рис. 3. Распределение электронов в проводящих заряженных телах.

Задача 3.

К проводящему кольцу приблизили точечный заряд Q так, чтобы он лежал в одной плоскости. Необходимо промоделировать перераспределение зарядов в кольце.

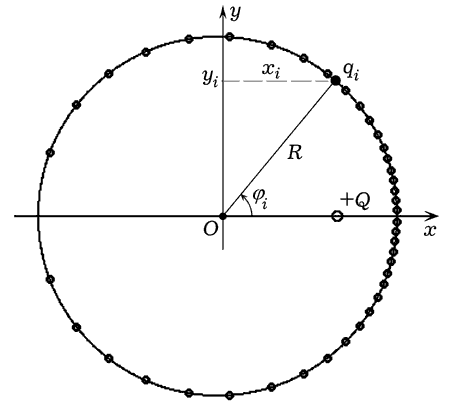
Рис. 4. Распределение электронов в кольце в поле точечного заряда.

Распределение зарядов в кольце симметрично относительно прямой, проходящей через его центр О и заряд Q (рис. 4). Рассмотрим совокупность из 2N точечных зарядов qi, равноудаленных от центра кольца О на расстояние R. Положение каждого заряда характеризуется углом φi, причем каждому i-ому заряду из верхней половыны кольца соответствует (i+N)-ый заряд из нижней половины.

Программа ПР-3.

Используемая программа ПР-3 работает так: случайным образом изменяются углы φi, каждый раз пересчитываются координаты зарядов и суммарная потенциальная энергия системы U. Если она уменьшается, то изменение φi принимается, а иначе -- отвергается. Результаты вычислений для случаев, когда заряд Q находится внутри кольца и вне его представлены на рис. 4 и 5.

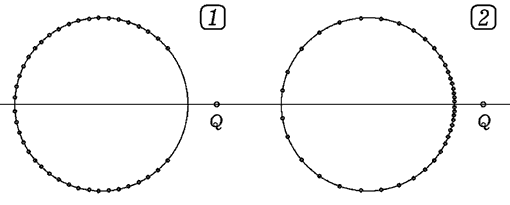
Рис. 5. Распределение электронов в кольце в поле точечного заряда.

Тексты программ находятся в zip-архиве, файл gl2-12.pas.

ВВЕРХ

Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net .