Задача 1. На смачиваемой горизонтальной поверхности висит капля жидкости. Необходимо рассчитать ее форму.

Решение известной задачи о расчете формы капли можно найти в книге В.А. Саранина "Равновесие жидкости и его устойчивость. Простая теория и доступные опыты", 2002 (с. 88 - 92). В ней показано, что форма осевого сечения капли, висящей под горизонтальной смачивающейся поверхностью в поле тяжести, определяется из дифференциального уравнения:

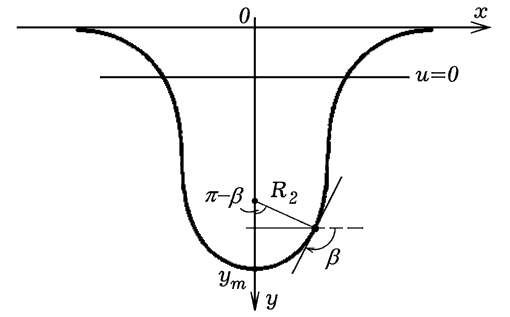
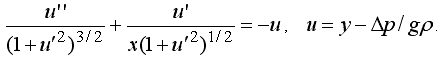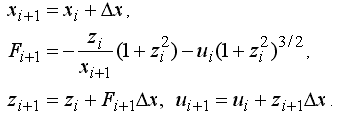Это обезразмеренное уравнение равновесия висящей капли (рис. 1), выполняющееся для любой жидкости и поля тяжести. Начало отсчета u=0 соответствует тому горизонтальному сечению капли, где кривизна ее поверхности равна 0. В той же книге приведена программа на языке Basic, решающая это уравнение.

Рис. 1. Форма осевого сечения капли (из книги В.А.Саранина).

Если использовать подстановку z=u', то уравнение равновесия висящей капли в конечных разностях будет выглядеть так:

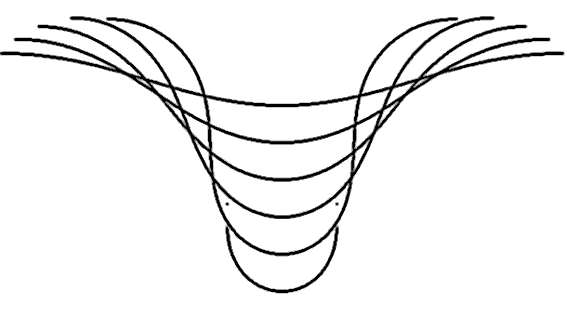
Для реализации этой конечно-разностной схемы используется программа ПР-1. Результаты расчетов для различных 6 начальных значений u (при x=0) представлены на рис. 2.

Программа ПР-1.

Рис. 2. Результаты расчетов формы капли.

Задача 2. Рассчитайте форму поверхности капли жидкости, лежащей на горизонтальной несмачивающейся поверхности.

Чтобы из висящей капли получить лежащую каплю, необходимо "перевернуть" горизонтальную поверхность с жидкостью так, что ось OY будет направлена вверх, противоположно ускорению свободного падения. Тогда z=-du/dx. Если поверхность не смачивается жидкостью, то капля похожа на сплюснутый шар и имеет верхнюю и нижнюю поверхности. В точках переход от нижней поверхности к верхней производная du/dx стремится к бесконечности.

Программа ПР-2.

Используемая программа ПР-2 состоит из двух частей, в которых по отдельности рассчитываются верхние и нижние поверхности капель различной формы. Результаты расчетов представлены на рис. 3 и 4. Если поверхность смачивается жидкостью, то капля имеет только верхнюю поверхность; достоточно использовать первую половину программы. Угол смачивания определяется начальным значением u.

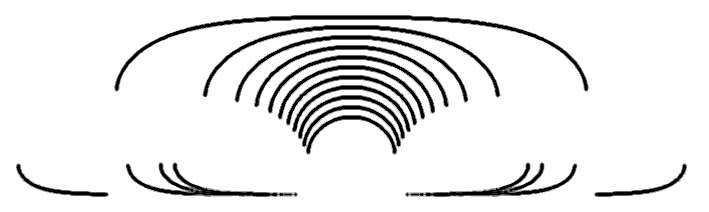
Рис. 3. Верхние и нижние поверхности капель, лежащих на несмачиваемой поверхности.

Рис. 4. Результаты расчета формы капель, лежащих на несмачиваемой и смачиваемой поверхности.

Тексты программ находятся в zip-архиве, файл gl2-4.pas.

Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net .