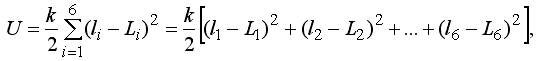РАСЧЕТ КОНСТРУКЦИЙ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ

Сущность метода конечных элементов (КЭ) состоит в следующем: конструкция или сплошная среда моделируется путем разбиения ее на конечные элементы (области небольшого размера). После этого формулируют и решают вариационную задачу о нахождении экстремали соответствующего функционала (например, потенциальной энергии). Метод КЭ используется при расчетах конструкций, поля температур, течений жидкости, электромагнитных полей и т.д. Рассмотрим несколько задач, решаемых методом КЭ. В них требуется промоделировать плоскую деформацию тела (конструкции), при которой его точки смещаются параллельно плоскости рисунка. В состоянии равновесия система имеет минимальное значение потенциальной энергии. Тело разбивают на стержневые или четырехугольные элементы. Программа содержит процедуру, в которой перебираются все элементы конструкции и вычисляется суммарная потенциальная энергия U системы. Узлы сетки смещаются на небольшие случайные величины, после чего еще раз рассчитывается потенциальная энергия U1. Если U1 меньше U, то эти смещения принимаются, а если нет -- отвергаются. Эта процедура повторяется многократно. В результате последовательности итераций определяется искомое состояние системы с наименьшим значением потенциальной энергии.

Задача 1.

Рассчитайте деформацию фермовой конструкции из 5 звеньев, к концу которой подвешен груз.

Для решения этой задачи следует использовать программу ПР-1, в которой перебираются все стержни, вычисляется их удлинение (сжатие) и суммарная потенциальная энергия системы U. Рассмотренным выше методом определяется ее состояние, при котором U минимально. Результат решения задачи -- на рис. 1.

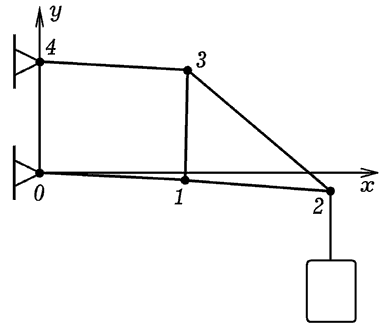
Рис. 1. Результаты расчета деформации фермы с грузом.

Рис. 1. Результаты расчета деформации фермы с грузом.

Программа ПР-1.

Задача 2.

В вертикальную стену вмонтирована горизонтальная балка (консольное закрепление). К ее концу привязан трос с грузом m1, перекинутый через неподвижный блок. К средней части балки подвешен груз m2. Необходимо рассчитать форму балки в состоянии равновесия.

От реальной конструкции перейдем к конечно-элементной аппроксимации. Сечение балки разобьем на четырехугольные элементы. Потенциальная энергия системы:

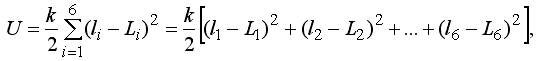
где L1, l1 (i= 1, 2, ..., 6) -- длины четырех сторон и двух диагоналей четырехугольного элемента в ненапряженном и деформированном состояниях, k -- коэффициент жесткости. При этом приближенно считается, что этот конечный элемент эквивалентен четырехугольнику, вершины которого соединены упругими стержнями. В отдельной процедуре рассчитывается суммарная энергия элементов 1-2-13-14, 2-3-12-13, 3-4-11-12 и т.д. К этому значению U прибавляется потенциальная энергия грузов m1gh1 +m2gh2. используется программа ПР-2, результаты моделирования -- на рис. 2.

Программа ПР-2.

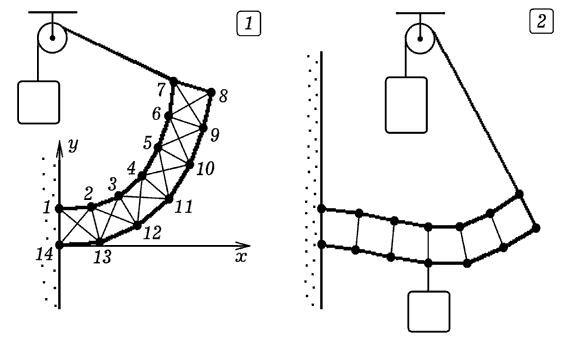
Рис. 2. Форма деформированной балки.

Рис. 2. Форма деформированной балки.

Задача 3.

К верхней части упругого вертикального стержня прикреплена горизонтальная жесткая балка AB длиной L, на конце которой расположен груз массы m. Рассчитайте форму стержня.

Пронумеруем вершины, как показано на рис. 3. Используемая программа ПР-3 представлена ниже. Координаты вершин четырехугольных элементов сохранены в массивах x[i], y[i]. С помощью функции вычисляется потенциальная энергия 6 стержней, соответствующих четырехугольнику с вершинами W(a1, a2, a3, a4), ai i=1, 2, 3, 4. В процедуре Pot_En рассчитывается суммарная потенциальная энергия всей системы, включая энергию груза на стержне AB (рис. 3).

Программа ПР-3.

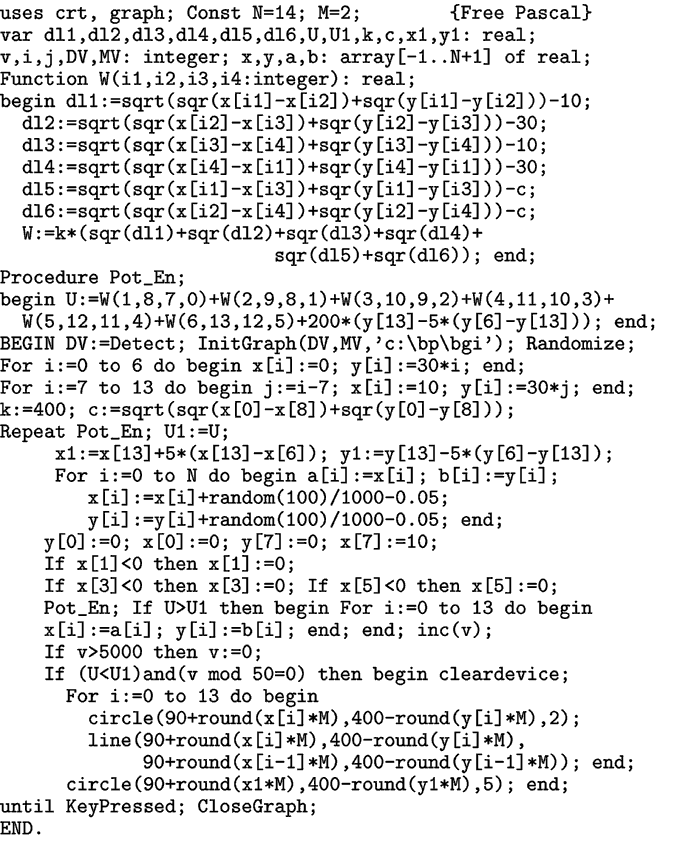
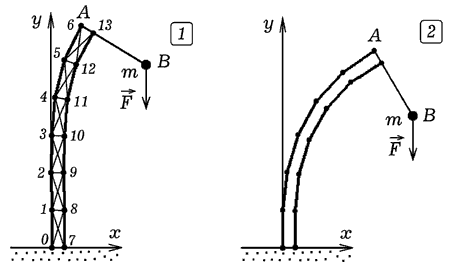
Рис. 3. Расчет деформации столба с грузом.

Рис. 3. Расчет деформации столба с грузом.

Задача 4.

К консоли переменного сечения приложены силы F1, F2 и F3, направленные вертикально вниз. Необходимо рассчитать форму консоли.

Задача решается аналогичным способом. Используется программа ПР-4. Результаты вычислений представлены на рис. 4.

Программа ПР-4.

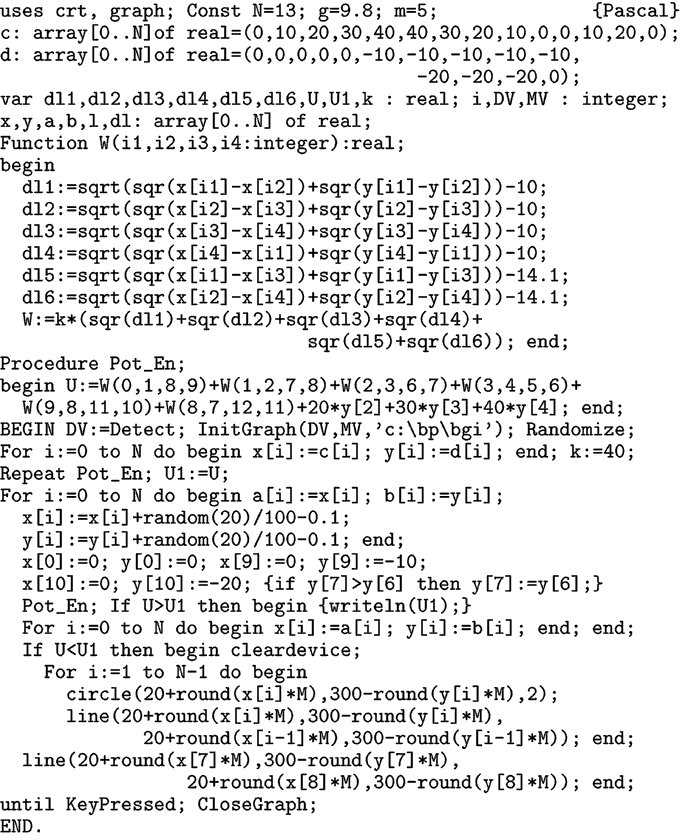
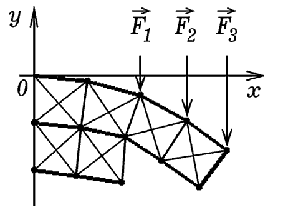
Рис. 4. Расчет деформации консоли переменного сечения.

Рис. 4. Расчет деформации консоли переменного сечения.

Задача 5.

Труба прямоугольного сечения из упругого материала сжимается с противоположных сторон. Рассчитайте ее форму при различных нагрузках.

Для решения задачи достаточно рассмотреть деформацию четверти трубы. Разбиение на элементы, нумерация вершин и результаты моделирования представлены на рис. 5 и 6. Тексты используемых программ ПР-5 и ПР-6 приведены ниже. Тем же способом может быть рассчитана форма П-образной пластины, к которой приложена механическая нагрузка.

Программа ПР-5.

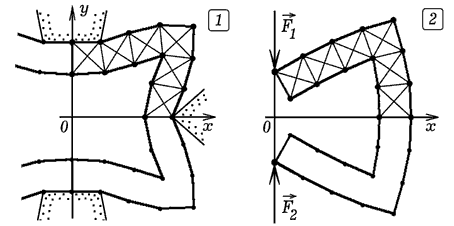
Рис. 5. Форма деформированной трубы прямоугольного сечения.

Рис. 5. Форма деформированной трубы прямоугольного сечения.

Программа ПР-6.

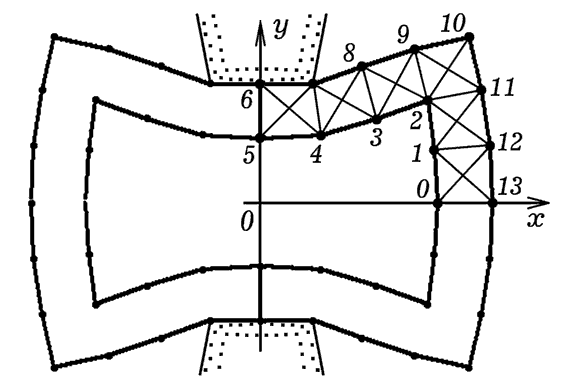
Рис. 6. Форма деформированной трубы прямоугольного сечения.

Рис. 6. Форма деформированной трубы прямоугольного сечения.

Задача 6.

Труба круглого сечения из упругого материала сжимается в вертикальном направлении. В горизонтальном направлении она ограничена вертикальными пластинами. Необходимо рассчитать ее форму при различных нагрузках.

Задача решается аналогично. Используется программа ПР-7, результаты расчетов -- на рис. 7 и 8.

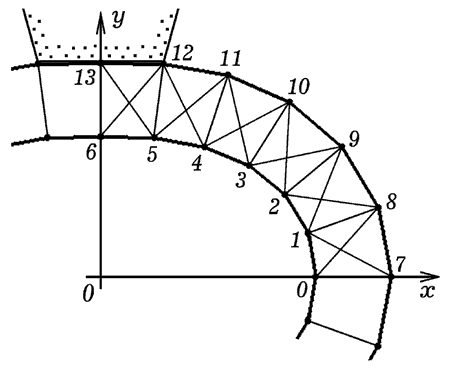
Рис. 7. Расчет деформации круглой трубы.

Рис. 7. Расчет деформации круглой трубы.

Программа ПР-7.

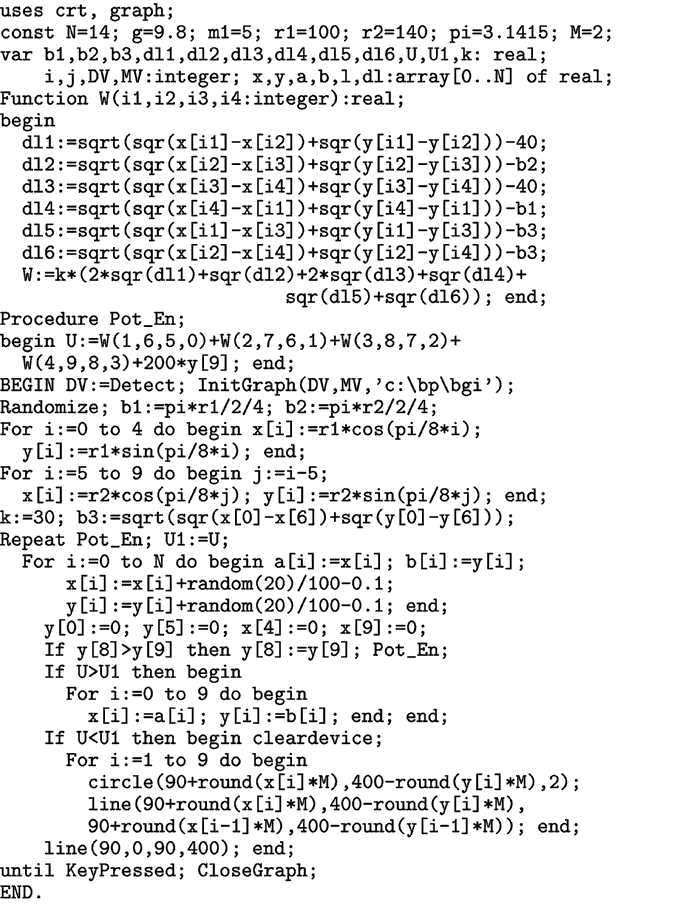
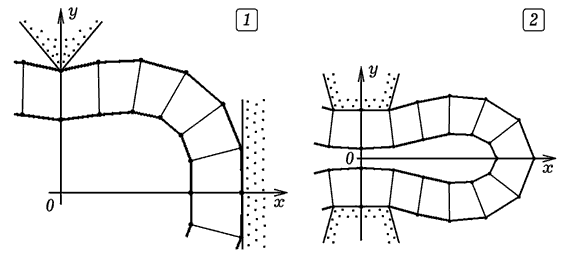
Рис. 8. Расчет деформации круглой трубы.

Рис. 8. Расчет деформации круглой трубы.

Задача 7.

На вертикальной плоскости находится прямоугольная пластина. Некоторые ее точки закреплены, а к другим точкам приложены вертикальные силы. Необходимо, используя метод конечных элементов, рассчитать форму пластины.

Разобьем пластину на квадратные элементы и пронумеруем вершины, как показано на рис. 9. Задача является двумерной, все точки пластины смещаются в плоскости XOY. Используемая программа ПР-8 представлена ниже. Координаты вершин четырехугольных элементов сохраняются в массивах x[i], y[i], а их начальные значения -- в массивах x0[i], y0[i]. С помощью процедуры Pot_En; вычисляется потенциальная энергия 6 стержней (4 стороны и 2 диагонали). Рассмотрены две ситуации: 1) узлы 0 и 5 закреплены, к узлам 27, 28, 29 приложены силы, направленные вниз (рис. 9.1); 2) узлы 0, 11, 12, 23 и 24 закреплены, к узлам 27, 28, 29 приложены силы, направленные вниз (Рис.9.2).

Программа ПР-8.

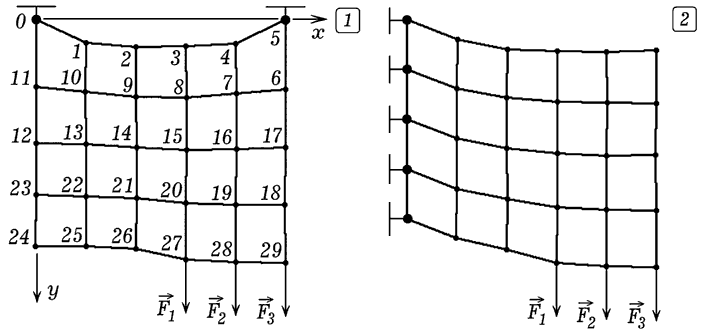
Рис. 9. Деформация плоской пластины.

Рис. 9. Деформация плоской пластины.

Программа ПР-8 позволяет рассчитать деформацию пластины при симметричной нагрузке (рис. 10). Чтобы решить эту задачу достаточно расмотреть левую половину пластины, у которой узлы 0, 11, 12, 23, 24 закреплены (координаты x и y остаются постоянными), а у узлов 5, 6, 17, 18, 29 координата x имеет фиксированное значение 50.

Рис. 10. Результаты расчета формы пластины.

Рис. 10. Результаты расчета формы пластины.

Задача 8.

В вертикальной плоскости за две точки подвешен прямоугольная упругая пластина (ткань) известной массы. К заданным точкам приложены силы определенной величины и направления. Необходимо рассчитать, какую форму примет упругая пластина под действием этих сил и сил тяжести.

Разобьем пластину на квадратные элементы и пронумеруем вершины также, как в предыдущей задаче. Используемая программа ПР-9 отличается тем, что в ней варьируются все три координаты x, y и z кждого узла. С помощью процедуры Pot_En; вычисляется потенциальная энергия 6 стержней (4 стороны и 2 диагонали). При этом учитывается, что на пластину действует сила тяжести (узлы имеют массу). Результаты моделирования представлены на рис. 10.

Программа ПР-9.

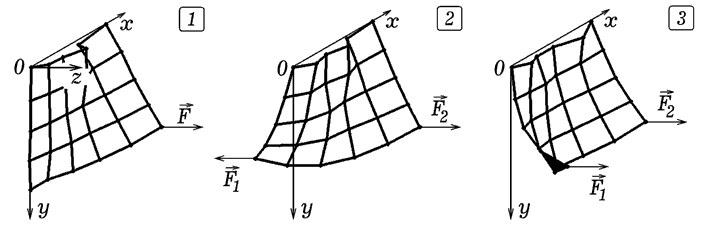
Рис. 10. Деформация упругой ткани подвешенной в вертикальной плоскости.

Рис. 10. Деформация упругой ткани подвешенной в вертикальной плоскости.

Тексты программ находятся в zip-архиве, файл g2-5.pas.

ВВЕРХ

Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net .