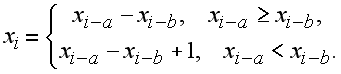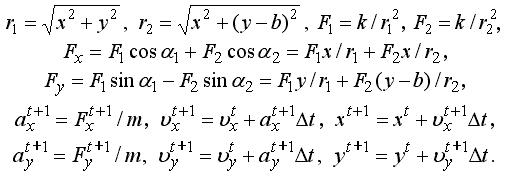Задача 1. Промоделируйте одномерные случайные блуждания молекулы газа, используя фибоначчиевый генератор случайных чисел. Получите распределение конечной координаты zN блуждающей точки при различном количестве совершенных шагов N. Убедитесь в том, что квадрат смещения случайной величины zN прямо пропорионален N.

Молекула из-за хаотических соударений с другими молекулами случайным образом движется вдоль оси координат. Будем использовать метод статистических испытаний. Программа ПР-1, моделирующая такое движение, содержит цикл, в котором случайным образом определяется направление и величина смещения молекулы на следующем временном шаге. Цикл совершает требуемое число итераций (равное количеству шагов N), в результате чего определяется конечная координата молекулы zN. Затем осуществляется новая реализация этого процесса, и так 1000 раз. При этом вычисляется дисперсия случайной величины zN и находится ее распределение.

Для генерации случайных величин, имеющих равномерное распределение, применяется метод Фибоначчи с запаздываниями. Он состоит в использовании следующей рекуррентной формулы:

Здесь x_i -- действительные числа из диапазона [0; 1], а a и b -- лаги (целые положительные числа), причем a больше b. Лаги специально подбираются так, чтобы в результате получалась равномерно распределенная случайная величина: a=55, b=24. Чем больше a, тем выше качество получающейся последовательности. Для работы этого генератора псевдослучайных чисел необходимо в памяти ЭВМ хранить a предыдущих случайных чисел. Преимущество этого метода в том, что он не требует умножения, а недостатки, -- необходимость большого объема памяти и исходного массива чисел для запуска программы.

Программа ПР-1.

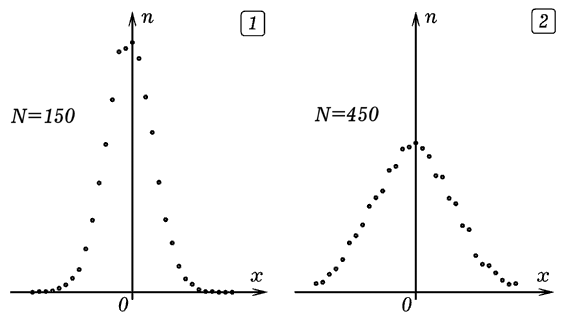
Рис. 1. Распределение z_N в результате 10000 испытаний (150 и 450 шагов).

На рис. 1 показаны получающиеся распределения конечной координаты молекулы z_N после 150 и 450 шагов (10000 испытаний). Видно, что получается нормальное распределение Гаусса. Можно отключить графический режим и вывести на экран квадрат дисперсии (СКО) z_N при заданном N. Если построить график квадрата смещения z_N от количества шагов N, то получится прямая пропорциональность (рис. 2).

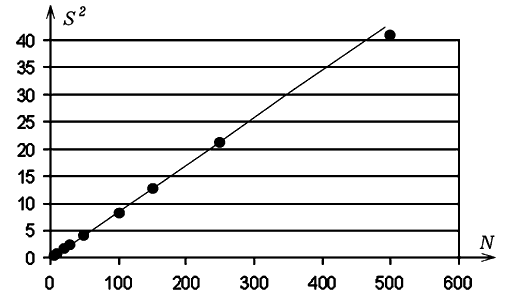
Рис. 2. Квадрат координаты z_N пропорционален числу шагов N.

Получающиеся результаты можно интерпретировать двояко: 1) с течением времени увеличивается область, в которой может находится хаотически движущаяся молекула; 2) если из небольшого объема выходит 10000 молекул некоторого вещества, то через некоторое время (пропорциональное количеству шагов N) молекулы вследствие диффузии расползутся и займут большую область. Программа моделирует одномерную диффузию молекул газа, которые изначально находились в небольшом объеме.

Задача 2. Создайте имитационную модель опыта Резерфорда по рассеянию альфа-частиц атомами золота. Рассчитайте траекторию движения частицы в поле отталкивания двух атомов. Методом статистических испытаний изучите зависимость числа альфа-частиц от угла отклонения при случайных значениях прицельного параметра.

Эксперимент Резерфорда состоял в следующем: на пути пучка альфа-частиц в вакууме располагалась тонкая золотая фольга и с помощью сцинтилляционного экрана иследовалось отклонение альфа-частиц от прямолинейного движения. Было обнаружено, что существенная часть альфа-частиц довольно сильно изменяют траекторию движения, а некоторые вообще отбрасываются назад (под углами близкими к 180o). Рассмотрим два ядра с зарядами +q, расположенных в точках с координатами (0; 0) и (0; b), которым подлетает альфа-частица. Прицельным параметр ρ отсчитывают, как показано на рис. 3.

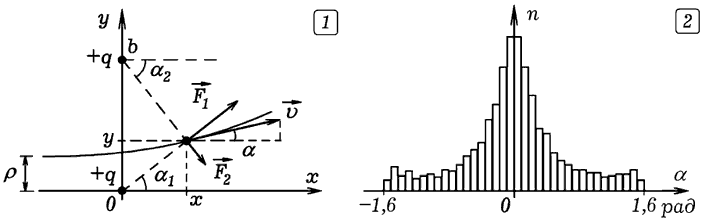
Рис. 3. Движение альфа-частицы в поле атомов золота.

Траектория движения альфа-частицы при заданном прицельном параметре (рис. 3.1) рассчитывается с помощью программы ПР-2, содержащей цикл по времени t, в теле которого закодированы формулы:

Угол отклонения альфа-частиц от первоначального направления движения раcсчитывается из формулы: α=arctg(v_y/v_x). В результате однократной реализации процесса получается значение угла α, соответствующее случайно выбранному ρ. В пучке находится много альфа-частиц, которые имеют всевозможные значения ρ. Поэтому в программе необходимо создать цикл, в котором прицельный параметр ρ изменяется случайным образом, каждый раз рассчитывается траектория движения альфа-частицы и определяется соответствующее отклонение α. На рис. 3.2 представлены результаты многократных испытаний, полученные при имитационном моделировании.

Программа ПР-2.

Задача 3. Имеется металлическая сетка M x M, расположенная между двумя электродами, из которой случайным образом с заданной вероятностью q удалены некоторые узлы или ячейки (а с вероятностью p=1-q заняты). При небольших q существует путь, соединяющий электроды, и сетка проводит ток. Необходимо изучить зависимость вероятности P возникновения перколяционного кластера, пронизывающего всю структуру, от вероятности p.

При больших q будет вырезано слишком много узлов, и исчезнет путь, соединяющий нижний электрод с верхним, -- сетка перестанет проводить ток. Если вырезано мало узлов, то будет существовать один или несколько перколяционных кластеров, пронизывающих данную структуру насквозь и соединяющих электроды. Этот переход из состояния, при котором нет соединяющего кластера в состояние, содержащее соединяющий кластер, является фазовым переходом. Проблема состоит в нахождении порога перколяции pc, то есть критического значения вероятности наличия узла p=1-q, при котором возникает хотя бы один кластер из бесконечного числа узлов.

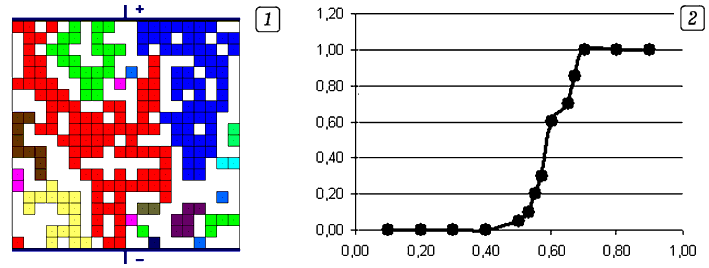
Совокупность занятых ячеек, связанных с ближайшими по стороне, образуют кластер. Две ячейки относятся к одному кластеру, если существует путь из занятых ячеек, соединяющий их друг с другом. На рис. 5.1 ячейки, входящие в один кластер закрашены одним цветом. Красные ячейки образую перколяционный кластер, пронизывающий всю структуру и соединяющий верхний и нижний электроды. Найдем зависимость вероятности образования перколяционного кластера от вероятности p наличия узла.

Для этого используется метод статистических испытаний, реализованный в программе ПР-3. Сначала, исходя из заданной вероятности p наличия занятой ячейки, случайным образом формируется ячеистая структура (рис. 4.1), после чего определяется, содержит она перколяционный кластер или нет. Эта процедура многократно повторяется, что позволяет определить вероятность перколяции P при данном значении p. Затем проводится аналогичный вычислительный эксперимент при других p и строится график зависимости P=P(p).

Для установления факта наличия или отсутствия перколяции создается список связности, в котором существующим (не вырезанным) узлам сетки, входящим в один кластер, присваивается один и тот же номер. Программа находит существующий узел (i,j) и присваивает ему номер кластера N_кл=1, который записывается в специальный массив g[k]. После этого перебираются все существующие узлы (ячейки), и если они являются смежными, то есть удалены от узла (i,j) на 1, то им тоже присваивается номер N_кл=1. Если узел существует (является смежным), то для него повторяют эту процедуру, находя все узлы смежные с ним. В результате все узлы, относящиеся кластеру с номером N_кл=1, получают номер 1, который хранится в массиве g[k].

После этого программа, перебирая все существующие узлы, находят любой узел, у которого номер N_кл=0, то есть он не отнесен к первому кластеру. Ему присваивается номер N_кл=2, и этот же номер получают все остальные существующие узлы, образующие с ним один кластер. После этого, снова перебирая все существующие узлы сетки, находят любой узел, у которого номер N_кл=0, то есть он не отнесен ни к первому, ни ко второму кластеру. Ему присваивают номер N_кл=3 и т.д.

Программа ПР-3.

Рис. 4. Изучение перколяции методом статистического моделирования (дискретная модель).

После того, как все занятые ячейки отнесены к тому или иному кластеру и имеют номера, записанные в массиве g[k], устанавливается факт существования перколяционного кластера. Перебирая все узлы, ищут такие два, для которых выполняются условия: 1) один узел контактирует с верхней пластиной (j=1), а другой с нижней (j=M); 2) оба узла относятся к одному и тому же кластеру, то есть имеют одинаковые номера N_кл. При перколяции на экран выводится 1, при ее отсутствии -- 0. Для нахождения вероятности P образования пронизывающего кластера процедура формирования новой ячеистой структуры и установления факта существования перколяции многократно повторяется. В программе ПР-7 выполняется S= 20-50 испытаний, получающиеся результаты выводятся на экран. Это позволяет оценить вероятность P перколяции при различных p и построить график (рис. 4.2). Из него видно, что с ростом p от 0,4 до 0,7 резко увеличивается вероятность перколяции P. Для увеличения статистической значимости результатов следует провести большее количество испытаний.

Задача 4. Внутрь квадратной области 100 x 100 случайным образом бросают N одинаковых металлических дисков радиусом R=4. Нижняя и верхняя стороны квадрата являются электродами, на которые подано напряжение. Необходимо изучить зависимость зависимость вероятности P замыкания электродов образовавшимся перколяционным кластером от количества дисков N.

Так как координаты центров проводящих кругов -- непрерывная величины, то и используемая модель перколяции называется непрерывной. Моделирующая программа ПР-4 содержит цикл, в котором случайным образом рассчитываются координаты N дисков, заполняющих рассматриваемую область. В следующем цикле перебираются все диски и создается список связности. Каждому i-ому диску ставится целочисленная переменная g[i], равная номеру кластера, к которому принадлежит данный диск. На последнем этапе устанавливается факт существования перколяционного кластера. Для этого перебираются все диски и ищется как минимум одна пара i и j, которые принадлежат к одному кластеру (g[i]=g[j]), причем один из дисков касается верхней стороны квадратной области (y[j] больше 100-R), а другой -- нижней (y[i] меньше R). Если хотя бы одна такая пара дисков существует, значит имеется перколяционный кластер, пронизывающий всю структуру, и на экран выводится цифра 1, а в противном случае -- 0.

Программа ПР-4.

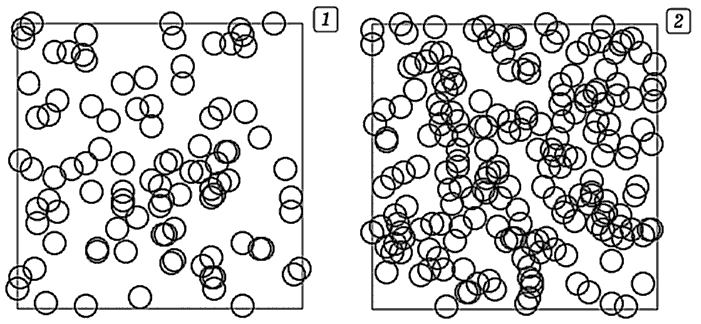
Результаты работы программы приведены на рис. 5. Видно, что при N=100 перколяция отсутствует (рис. 5.1), а при N=200 возникает перколирующий кластер (рис. 5.2). Для того, чтобы изучить зависимость вероятности возникновения перколяционного кластера от числа дисков, используют метод статистических испытаний. Необходимо дополнить программу так, чтобы она моделировала многократное проведение серии опытов, в которых бросаются N₁ дисков и определяется вероятность перколяции при N=N₁. Такая программа позволит определить вероятность P при других N₂, N₃, N₄ и построить график P=P(N).

Рис. 5. Образование перколяционного кластера (непрерывная модель).

Рассмотренные дискретная и непрерывная модели перколяции, имеют большое значение для теории перколяции (просачивания или протекания). Эта теория описывает физические процессы, происходящие в неоднородных средах со случайными свойствами. К ней относятся исследования электропроводности композиционных материалов, состоящих из проводящих и непроводящих компонентов, изучения фазовых переходов газа в жидкость, образования магнитных доменов, диффузии в неупорядо-ченных средах и т.д.

Задача 5. Источник вырабатывает сообщение 10110010: Кодер разбивает его на блоки длиной D-1 и добавляет 1 бит четности так, что получаются кадры длиной D. Они поступают в канал связи, в котором с вероятностью p вносятся ошибки (инвертируются биты), и, пройдя через него, попадают в декодер. На передачу 1 бита затрачивается 1 такт машинного времени (допустим, 1 мс). Реализуется система с переспросом: декодер выявляет кадры с ошибками и по каналу переспроса посылает сигнал о повторе передачи соответствующего кадра. На его повторную передачу снова затрачивается N тактов. Сигнал по каналу переспроса не вносит задержки. Промоделируйте этот процесс на ПЭВМ, определите скорость передачи.

Для компьютерного моделирования используется программа ПР-5. Длина кадра D равна величине константы Dlina_k, при этом число информационных бит составляет D-1, число кадров равно Chislo_k= 500. В программе организован цикл, в котором моделируется покадровая передача информации. При каждой итерации время t увеличивается на D.

Программа ПР-5.

В кадре длиной D происходит ошибка с вероятностью pD. Генерируется случайное число x и если оно меньше pD, то происходит ошибка и по каналу связи повторно передается тот же кадр (для этого i уменьшается на 1). При безошибочной передаче кадра на экран просто выводится время t. Скорость передачи определяется так: v= Chislo_k (D-1)/t, где (D-1) -- число информационных бит, t -- число тактов. Она зависит от длины кадров и вероятности ошибки p.

В случае, когда длина кадра D=8, и сообщение передается без помех (p=0), cскорость передачи полезной информации в результате моделирования получается равной v=0,875 бит/c. В самом деле, к семи информационным битам прибавляется восьмой проверочный, поэтому скорость передачи можно рассчитать так: v=7/8= 0,875. Проведя серию вычислительных экспериментов можно убедиться, в том что при увеличении вероятности p ошибки скорость v передачи информации уменьшается: 1) при p=0,001, v=0,867 бит/с; 2) при p=0,01, v=0,800 бит/с; 3) при p=0,02, v=0,724 бит/с; 4) при p=0,05, v=0,522 бит/с.

Задача 6. Используя компьютерную модель, изучите зависимость скорости передачи информации по каналу связи от вероятности ошибки p, постройте графики. Длина кадра равна: 1) 4 бит; 2) 8 бит.

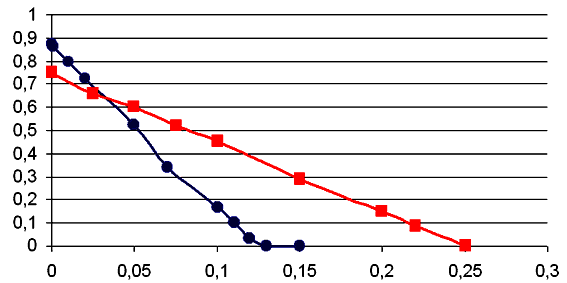
Используется программа ПР-5. При увеличении вероятности ошибки растет частота переспросов, скорость передачи информации уменьшается. Поэтому графиком зависимости v=v(p) является убывающая кривая, которая с увеличением p приближается к 0 (рис. 6). Если длина кадра D=8, то уже при p=1/8=0,125 каждый кадр будет содержать ошибку, поэтому передать информацию не удастся (v=0). Для кадров длиной D=4 такая ситуация наступает при p=1/4=0,25.

Рис. 6. Зависимость скорости передачи от вероятности ошибки: 1) длина кадра D=8 (красный); 2) длина кадра D=4 (синий).

Задача 7. Постройте график зависимости скорости передачи информации от длины кадра, если вероятность ошибки постоянна и равна 0,02; 0,1; 0,3.

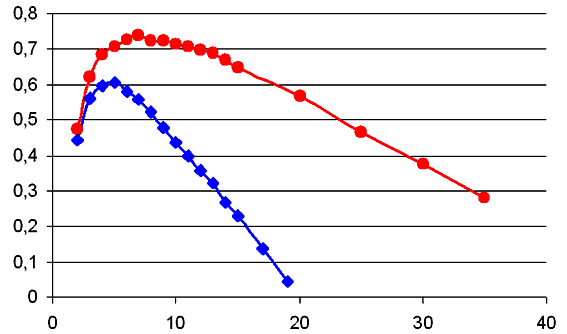
Используется программа ПР-5. Если p= 0,1, то при длине кадра 2 или 3 бита скорость передачи невелика за счет большого числа проверочных битов четности. С ростом длины кадра она уменьшается из-за увеличения вероятности ошибки в кадре и затрат времени на повторную его передачу. Существует некоторая оптимальная длина кадра, при которой скорость максимальна. Результаты моделирования -- на рис. 7.

Рис. 7. Зависимость скорости передачи от длины кадра D при вероятностях ошибки: 1) p=0,02 (красный); 2) p=0,05 (синий).

Задача 8. Считая, что емкость канала связи C равна максимальной скорости передачи информации, изучите зависимость емкости канала от вероятности ошибки, постройте график. Сравните полученные результаты с расчетными значениями для двоичного симметричного канала с шумом.

Емкость (пропускная способность) двоичного симметричного канала связи с вероятностями ошибки p и правильной передачи (1 - p) равна C=C0(1+plog2p+(1-p)log2(1-p)). При p = 0 (ошибок нет) емкость канала максимальна и равна C0=1; когда p = 0,5, емкость канала C=0. Используется программа ПР-8. Для нахождения емкости C моделируемого канала связи с переспросом зададим вероятность ошибки 0,05 и найдем скорости передачи при различных длинах кадра. Обнаружим, что при N = 5 скорость передачи максимальна и равна 0,60, -- эту величину и следует приближенно считать емкостью канала связи C. Повторим эту процедуру при других p, каждый раз определяя максимальную скорость передачи.

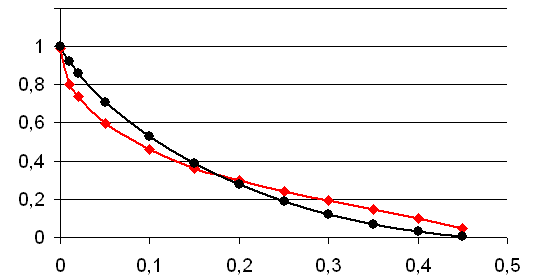
Рис. 8. Зависимость емкости канала связи от вероятности ошибки (черный цвет -- теория, красный -- моделирование).

Построим график зависимости емкости моделируемого канала связи от вероятности ошибки (рис. 8). Видно, что при увеличении p от 0 до 0,5 она уменьшается от 1 до 0. Эта зависимость похожа на расчетную кривую для двоичного симметричного канала связи, но точного совпадения нет.

Задача 9. Напишите программу, которая кодирует сообщение "1101011.." используя (5,2)--код, а затем осуществляет декодирование. При этом блок из 2 символов кодируется блоком из 5 символов по правилу: a1=x1, a2=x1, a3=x1 XOR x2, a4=x2, a5=x2. Декодирующая функция: b'=b1 XOR b3 XOR b5, y1=b1 XOR (b1 XOR b2)b', y2=b5 XOR (b5 XOR b4)b'. Промоделируйте передачу сообщения по каналу с шумом, в котором с заданной вероятностью q инвертируются биты.

Решением этой задачи является программа ПР-6. При ее запуске на экран выводится исходное сообщение, закодированное сообщение после кодера (перед каналом связи), сообщение с ошибками после канала связи и декодированное сообщение после декодера.

Программа ПР-6.

Тексты программ находятся в zip-архиве, файл gl2-6.pas.

Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net .