Задача 1. Создайте многокомпонентную модель обучения, учитывающую тот факт, что различные знания усваиваются с различной прочностью и забываются с разными скоростями. При достаточно долгом изучении какого вопроса вместе с ростом общего количества знаний происходит еще один процесс: приобретенные знания становятся более прочными и забываются медленнее. Промоделируйте процесс обучения на ПЭВМ.

Процесс усвоения и запоминания сообщаемой информации состоит в установлении ассоциативных связей между новыми и имеющимися знаниями. В результате приобретенные знания становятся более прочными и забываются значительно медленнее. Автором этой книги предложена многокомпонентная модель обучения, которая выражается системой уравнений:

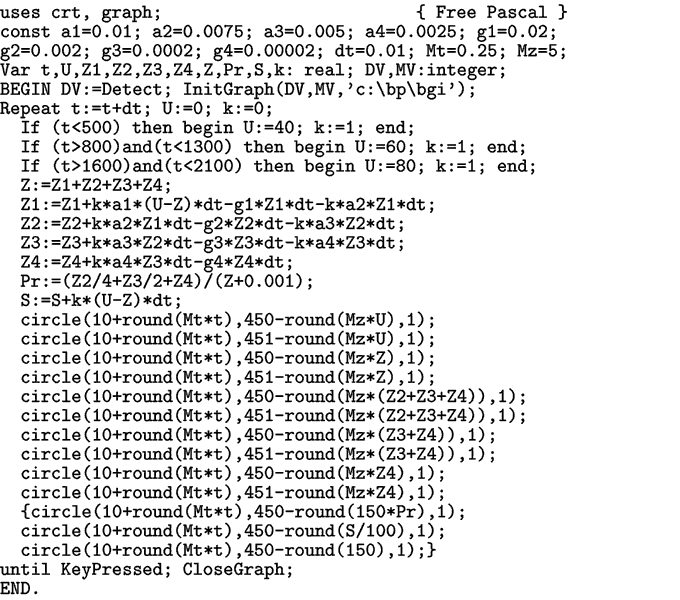
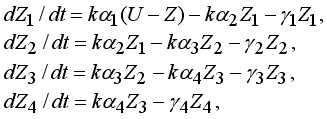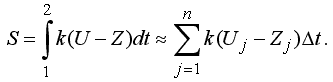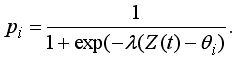где U –– уровень требований, предъявляемый учителем, равный сообщаемым знаниям Z₀, Z –– суммарные знания, Z₁ –– самые “непрочные” знания первой категории с высоким коэффициентом забывания γ₁ (гамма), а Z₄ –– самые “прочные” знания четвертой категории с низким γ₄ (γ_i+1 меньше γ_i, i= 1, 2, 3). Коэффициенты усвоения α_i (альфа) характеризуют быстроту перехода знаний (i-1)–ой категории в знания i–ой категории. Пока происходит обучение, k=1, а когда оно прекращается k=0. Коэффициент забывания γ_i=1/τ_i, где τ_i –– время, в течение которого количество знаний i–ой категории уменьшается в e = 2,72... раза. Результат обучения характеризуется не только суммарным уровнем приобретенных знаний Z= Z₁+ Z₂+ Z₃+ Z₄, но и коэффициентом “прочности”: Pr=(Z₂/4+ Z₃/2+Z₄)/Z. При изучении одной темы сначала растет уровень знаний Z₁, затем постепенно происходит увеличение количества более прочных знаний Z₂, Z₃, Z₄. При этом повышается прочность Pr.

Программа ПР-1.

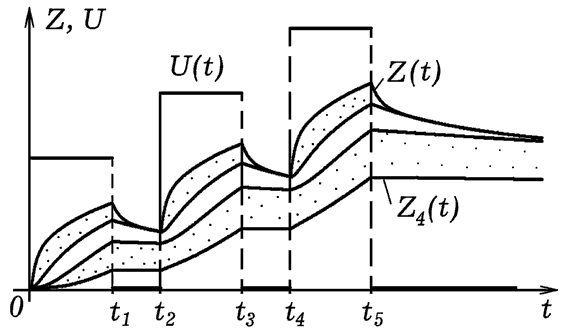
Рис. 1. Четырехкомпонентная модель обучения.

При использовании компьютерной программы ПР-1 получаются результаты, представленные на рис. 1. Уровень требований в течение каждого из трех занятий остается постоянным, уровень усвоенных знаний и их прочность возрастают.

Задача 2. Промоделируйте процесс обучения учащегося в течение трех занятий с помощью двухкомпонентной модели. Длительности занятий и перерывов между ними, а также уровень предъявляемых требований U в течение каждого занятия растет пропорционально времени.

Для исследования двухкомпонентной модели обучения используется программа ПР-2, результаты имитационного моделирования -- на рис. 2. Учитель проводит три урока, в течение которых уровень требований растет пропорционально времени: U=a(t-t0)+b. Видно, что во время перерывов и после обучения уровень "непрочных" знаний Z1 быстро уменьшается, а прочные знания Z2 забываются существенно медленнее.

Программа ПР-2.

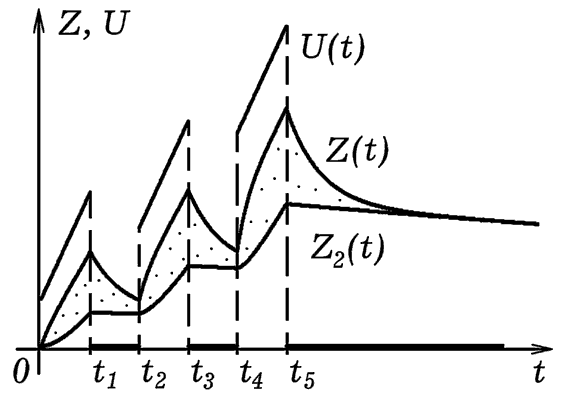
Рис. 2. Двухкомпонентная модель обучения.

Задача 3. Обучение осуществляется в согласованном режиме, когда уровень требований оптимален, учащийся работает достаточно интенсивно, мотивация к обучению не исчезет. Учитель проводит три занятия одинаковой длительности T, начинающиеся в фиксированные моменты времени t1, t2, t3. Необходимо определить длительность T занятий, при которой уровень знаний после обучения в момент t' будет равен Z''.

При согласованном обучении уровень требований учителя превышает знания учащегося на максимально возможную величину, при которой у учащегося не пропадает мотивация к учебной деятельности. Для нахождения эффективного пути обучения, соответствующего минимальным затратах энергии учителя и учащегося, в качестве целевой функции рассматриваемой оптимизационной задачи возьмем функционал:

Нагрузка на учащегося должна быть равномерно распределена по всем занятиям так, чтобы не было переутомления. Поэтому для каждого занятия продолжительностью Δt нужно вычислять затраты энергии S_i=k(U-Z)Δt и сравнивать их с пороговым значением. Кроме того, можно потребовать, чтобы уровень сформированности "прочных" знаний составлял, допустим, не менее 70 % от уровня Ur.

Программа ПР-3.

Для решения этой многокритериальной оптимизационной задачи использовалась программа ПР-3, содержащая цикл, в котором случайным образом изменяется длительность урока T, затем пересчитывается Z и выясняется, приблизился уровень знаний к требуемому значению или нет. Если да, –– изменения T принимаются, если нет, –– отвергаются, и все повторяется снова. Результаты оптимизации представлены на рис. 3.

Рис. 3. Нахождение оптимальной длительности занятий T.

Задача 4. Учитель проводит пять занятий заданной длительности T, начинающиеся в фиксированные моменты времени ti, i=1, 2, 3, 4, 5. В течение каждого занятия уровни требований Ui остаются постоянными. Необходимо подобрать такие Ui, чтобы уровень знаний учащегося достиг заданного значения Z''.

Для решения задачи используется программа ПР-4. В ней варьируются уровни требований U1, U2, U3, U4, U5 и подбираются такие Ui, при которых уровень знаний учащегося достиг заданного значения Z''. Результаты имитационного моделирования представлены на рис. 4.

Программа ПР-4.

Рис. 4. Нахождение оптимальных значений U_i.

Задача 5. Учитель обучает ученика решать N задач возрастающей сложности. Для этого он расположил задачи в порядке возрастания сложности и задает их ученику через промежутки времени Δt. Если ученик не решил задачу, то учитель обучает, а затем снова предлагает решить такую же задачу. Необходимо изучить зависимость количества знаний ученика от времени.

Будем считать, что сложность θi i-ой задачи равна количеству знаний Z, требующихся для ее решения. Учитель располагает N=10 задач в порядке возрастания сложности и задает их ученику через равные промежутки времени Δt. Если ученик не решил i-тую задачу, то учитель его обучает в течение времени Δt, а затем снова предлагает эту же или аналогичную задачу той же сложности θi. Если общее количество знаний Z больше или равно θi, то ученик решает задачу в течение времени Δt, Z не увеличивается, но часть "непрочных" знаний становится "прочными". После этого учитель предъявляет ему (i+1)-ую задачу с более высоким уровнем сложности θi. Если у ученика знаний меньше чем θi, то он не может решить задачу сразу. Учитель в течение времени Δt объясняет материал, уровень требований U=θi, знания Z1 и Z1 растет. Затем ученик снова пробует решить задачу. Занятия длительностью TЗ чередуются переменами продолжительностью TП, которые много больше Δt.

Программа ПР-5.

Для моделирования используется программа ПР-5, в ней решение задачи рассматривается как случайный процесс, вероятность которого вычисляется по формуле Роша:

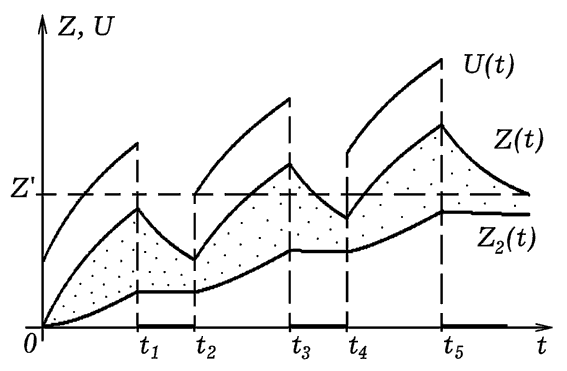
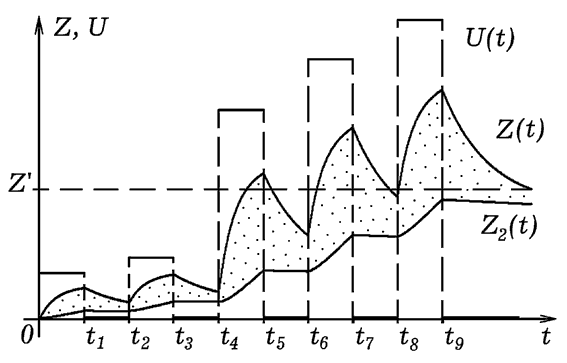
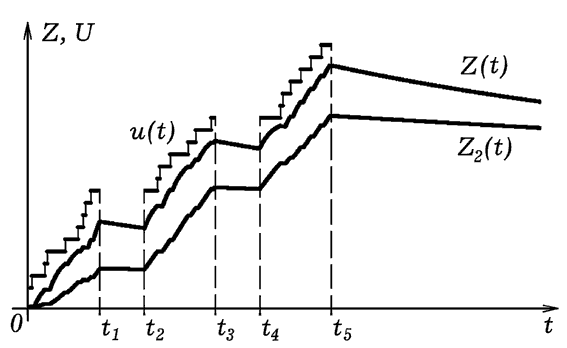
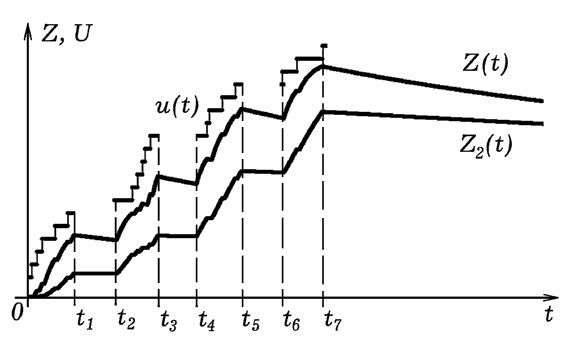
Результаты имитационного моделирования обучения на трех и четырех занятиях представлены на рис. 5. Ступенчатая линия показывает, как меняется сложность θ(t) решаемых задач; графики Z(t), Z₁(t) и Z₂(t) характеризуют динамику роста “непрочных” и “прочных” знаний. Рассмотренные имитационные модели позволяют проанализировать различные ситуации, возникающие в процессе обучения, выявить и обосновать описывающие их закономерности.

Рис. 5. Модель обучения путем решения задач возрастающей сложности.

Задача 6. Решение учебной задачи требует выполнения N операций в правильной последовательности. Сначала учащийся необучен, вероятности верного выполнения операций малы и равны 0,1. Учащийся решает последовательность задач, ошибается и, видя неверный результат, обращается за помощью к учителю. Тот проверяет решение и находит число правильно выполненных операций, сообщая об этом ученику. После этого ученик либо начинает решать задачу сначала, либо пытается закончить решение задачи, выполняя следующие операции. Промоделируйте этот процесс на ЭВМ.

При решении сложной задачи учащийся ведет себя как вероятностный автомат (ВА), осуществляющий ту или иную последовательность операций из некоторого множества O ={01, 02, ..., 0N}. Пусть решение всегда начинается с операции 1; последовательность 1 --> 2 --> 3 --> N является правильной. Вероятность выбора операции 2 после 1 обозначим p1, выбора (i+1)-ой операции после i-ой -- pi. Решение задачи аналогично поиску выхода из лабиринта. Все операции ВА совершает безошибочно; если же он допускает ошибку, значит выполняет какую-то другую операцию. Вероятность решения задачи с первой попытки равна произведению p1p2p3 ... . Если алгоритм решения известен, то pi=1, и ВА ведет себя как детерминированный автомат, достигая результата за минимальное число шагов.

В начале обучения вероятности p_i правильного выполнения (i+1)-ой операции после i-ой операции малы и равны 0,1. Ученик приступает к решению s-ой задачи. При правильном выборе первой операции, он переходит ко второй и т.д. На каждый шаг затрачивается одинаковое время Δt. Допустим, он ошибся и продолжает двигаться по неправильному пути. ВА совершает заданное количество шагов k (k>N), и, видя неверный результат, обращается к учителю. Учитель в течение времени Δt проверяет решение и находит число j первых правильно выполненных операций. Он сообщает ученику, что операции 1, 2, 3, ,.., j выполнены правильно и подсказывает (j+1)-ую операцию. В результате этого подкрепления и подсказки соответствующие вероятности p_i (i=1,2,3,...,j,j+1) правильных переходов увеличиваются на a(1-p_i). После этого ученик либо возвращается к операции 1, либо пытается закончить решение задачи, выполняя (j+1), (j+2) и последующие операции. В случае ошибки он снова обращается к учителю.

После того, как задача решена правильно, происходит подкрепление, и вероятности p_i (i= 1, 2, ..., N) выбора правильных действий увеличиваются на a(1-p_i). Вычисляется вероятность решения задачи P=p₁p₂... p_N, характеризующая степень обученности ученика. Затем он приступает к решению следующей задачи того же типа и все повторяется.

Программа ПР-6.

Программа ПР-6, моделирующая решение задачи, представлена выше. Номер выполняемой операции сохраняется в массиве O[i]. При правильном решении O[1]=1, O[2]=2, ... O[N]=N. Если допущена ошибка в выборе k-ой операции, то O[k]= -1. На экране строится графики зависимостей номера выполняемой операции и вероятности решения задачи от времени. Когда решение задачи не потребовало вмешательства учителя первый график имеет вид возрастающей прямой, идущей от первой к N-ой операции. При наличии ошибок в решении этот график будет содержать горизонтальные участки. Графиком зависимости вероятности правильного решения от времени является логистическая S-кривая. Чтобы промоделировать ситуацию, когда учащийся после обнаружения ошибки не продолжает решать задачу, а возвращается к первой операции, необходимо в программе раскомментировать оператор: {Если j меньше N, то j:=1;}.

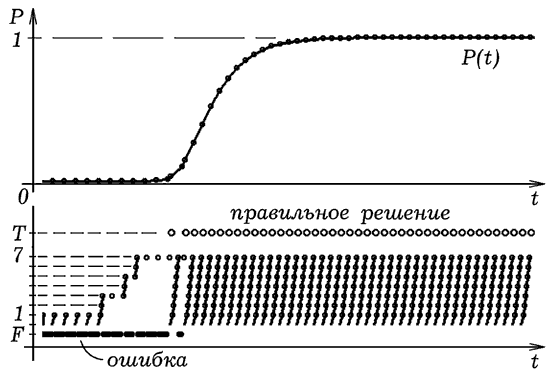
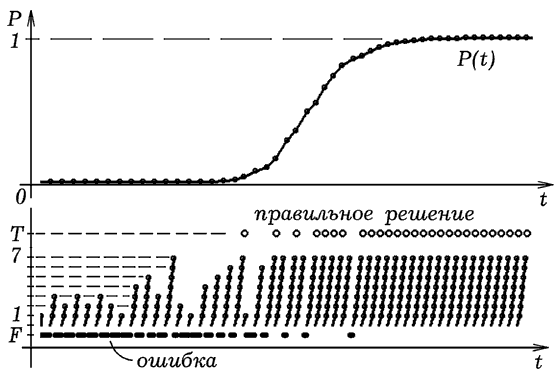
Рис. 6. Модель решения задачи учащимся (стратегия 1).

На рис. 6 и 7 представлены типичные результаты имитационного моделирования решения сложной задачи для двух стратегий поведения: 1) учащийся после совершения и ошибки и подсказки учителя продолжает решать данную задачу (рис. 6); 2) учащийся возвращается к началу решения задачи (рис 7). При запуске программа рисует ступенчатую кривую, показывающую, как изменяется номер выполняемой учащимся операции, и строит график зависимости вероятности решения задачи данного типа от времени P=P(t). В случае ошибки учащегося ПЭВМ ставит точку на уровне F (FALSE). Если задача решена правильно и до конца, то ПЭВМ ставит точку на уровне T (TRUE). Видно, что в обоих случаях формирование навыка происходит в соответствии с логистической функцией, графиком зависимости P(t) является S-кривая. В первом случае формирование навыка происходит заметно быстрее, чем во втором. Это объясняется тем, что каждый раз возвращаясь к началу решения (стратегия 2), ученик сначала учится выполнять операции 1, 2, 3 и не может сразу приступить к выполнению операций 4, 5, 6, 7. В первом случае учащийся одновременно усваивает все операции.

Рис. 7. Модель решения задачи учащимся (стратегия 2).

Задача 7. Создайте компьютерную программу, моделирующую решение учащимся некоторой задачи (движение в лабиринте). Вероятности правильного выполнения операций заданы.

Для того, чтобы оценить среднее время решения задачи данного типа используется метод статистических испытаний. Создается компьютерная модель вероятностного автомата, который моделирует движение учащегося по некоторому пути в лабиринте. В одном случае автомат выполняет шагов в некотором направлении (проходит несколько узлов лабиринта) и, если ему не удается получить ответ (выйти из лабиринта), возвращается к началу пути. Затем повторяет все снова и так N раз. В другом случае ВА, моделирующий деятельность учащегося, перед каждым шагом "решает", следует выполнять новое действие или лучше вернуться к началу -- операции 1. Используется программа ПР-7.

Программа ПР-7.

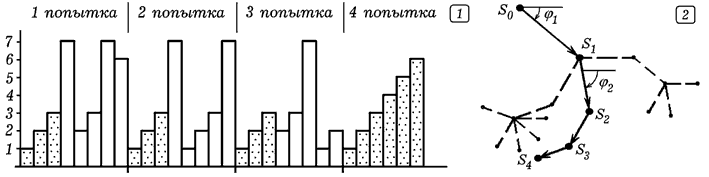
Результаты моделирования -- на рис. 8.1; по вертикали откладывается номер операции. Последняя попытка соответствует правильному пути 1 --> 2 --> 3 --> ... --> 6. ВА не обучается, при фиксированных вероятностях p_i время T_з (число шагов n) решения задачи, -- случайная величина. Чтобы определить среднее значение T_з, использовался метод статистических испытаний. В программу добавляют цикл, в котором 500 раз запускается вероятностный автомат, решающий задачу. Подсчитывается общее число шагов, число отказов от решения, после чего результаты усредняются.

Рис. 8. Моделирование решения задачи учащимся.

Чтобы построить граф решения (рис. 8.2), от начальной точки S₀, соответствующей начальному состоянию, откладывается вектор S₀S₁ длиной L₁=1 под углом φ₁= jΔφ к горизонтали, где j - номер операции. Затем от точки S₁ откладывается вектор S₁S₂ длиной L₂=1/2 под углом φ₂= jΔφ к горизонтали и т.д. В результате перебора всех различных сочетаний и последовательностей операций получается граф, имеющий фрактальную структуру. Правильному решению задачи соответствует некоторый путь из состояния S₀ в состояние S_N, где N -- число операций.

Тексты программ находятся в zip-архиве, файл gl2-7.pas.

Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net .