ОПТИМИЗАЦИЯ ПРОЦЕССА ОБУЧЕНИЯ

Задача 1.

Учащийся изучает N=3 темы, и по каждой из тем учитель может решить различное число задач. Время обучения ограничено, общее количество задач, которое решает учащийся, M=200. Коэффициенты усвоения второй и третьей тем зависят от уровней знаний Z1 и Z2 следующим образом: a2=a1Z1/2, a3=a1Z2. Все темы имеют одинаковую важность: V1=V2=V3=1. Необходимо найти такое распределение задач, при котором результаты тестирования в конце обучения максимальны. Забыванием пренебречь.

Допустим, на решение одной задачи затрачивается время Δt, при этом вероятность решения учащимся задачи данного типа повышается на Δp=a(1-p), где a - коэффициент научения. Уровень знаний Zi i-ой темы равен вероятности pi решения задачи по i-ой теме. В общем случае сложность задач i-ой темы зависит от уровня овладения предыдущих тем. При этом коэффициент научения ai, соответствующий i-ой теме, с ростом уровня знаний Zj (j меньше i) увеличивается (например, a3=kZ1+0,1). В конце обучения проводится тестирование, его результат равен T= V1Z1+ V2Z2+ V3Z3, где V1, V2, V3 -- коэффициенты важности, характеризующие степень значимости изученных тем. Необходимо найти оптимальную последовательность решения задач (функцию U(t)), при которой результат тестирования T в конце обучения максимален. Будем использовать метод имитационного моделирования.

Для решения этой оптимизационной задачи используется программа ПР-1. В ней случайным образом перебираются различные пути изучения этих тем (последовательности решения задач) и на каждом шаге выбирается тот, при котором T больше. Результаты оптимизации при a1=0,025 представлены на рис. 1.1, а при a1=0,05 -- на рис. 1.2. В интервале [0, t1] следует решать задачи из темы 1, в интервале [t1, t2] -- задачи из темы 2, а в интервале [t2, t3] -- задачи из темы 3. Во втором случае коэффициенты усвоения в два раза больше, поэтому и результаты тестирования после выполнения того же числа задач выше. Оценки за тест: T1=1,91, T2=2,74, при Tmax=3.

Программа ПР-1.

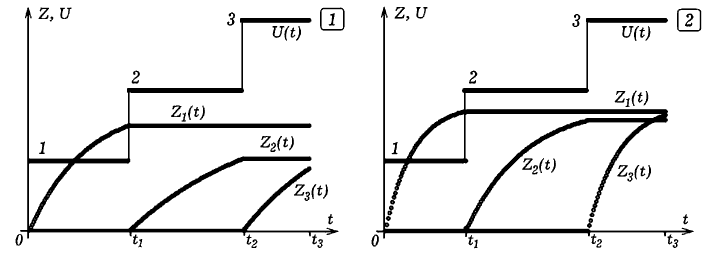
Рис. 1. Результаты оптимизации процесса обучения.

Рис. 1. Результаты оптимизации процесса обучения.

Задача 2.

Учащийся изучает N=3 темы, и по каждой из тем учитель может решить различное число задач. Время обучения ограничено, общее количество задач, которое решает учащийся, M=200. Коэффициенты усвоения тем: a1= 0,025, a2=a1Z1, a3=a1(Z1+Z2). При тестировании проверяются знания только третьей темы: V1=V2, V3=1. Необходимо найти такое распределение задач, при котором результаты тестирования в конце обучения максимальны.

Задача решается тем же способом, используется программа ПР-1. Результаты оптимизации U(t) представлены на рис. 2.1. Оценка за тест T1=0,97 при Tmax=1.

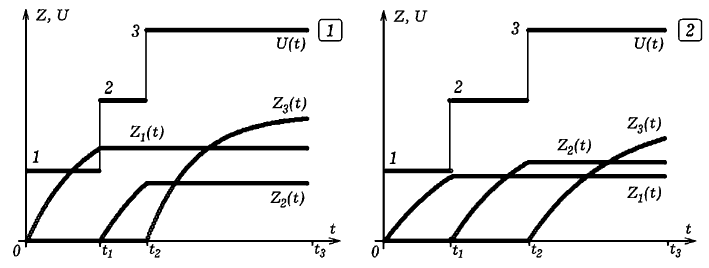
Рис. 2. Результаты оптимизации процесса обучения.

Рис. 2. Результаты оптимизации процесса обучения.

Задача 3.

Учащийся изучает N=3 темы, и по каждой из тем учитель может решить различное число задач. Время обучения ограничено, общее количество задач M=200. Коэффициенты усвоения тем: a1= 0,015, a2=0,015 Z1+0,01, a3=0,015(Z1+Z2). При тестировании проверяются знания только третьей темы: V1=0, V2=1, V3=5. Необходимо найти такое распределение задач, при котором результаты тестирования в конце обучения максимальны.

Результаты оптимизации представлены на рис. 2.2. Оценка за тест T=4,69, Tmax=6.

Задача 4.

Учащийся изучает N=6 темы, и по каждой из тем учитель может решить различное число задач. Время обучения ограничено, общее количество задач M=200. Коэффициент усвоения (i-1)-ой темы пропорционален уровню знаний предыдущей i-ой темы: a1= 0,04, a2= 0,04Z1, ai= 0,04Zi-1. Тест проверяет знания шестой темы; коэффициенты важности равны: V1=V2=...=V5=0, V6=1. Необходимо найти такое распределение задач, при котором результаты тестирования в конце обучения максимальны.

Результаты оптимизации -- на рис. 3.1. Оценка за тест T=0,67, Tmax=1.

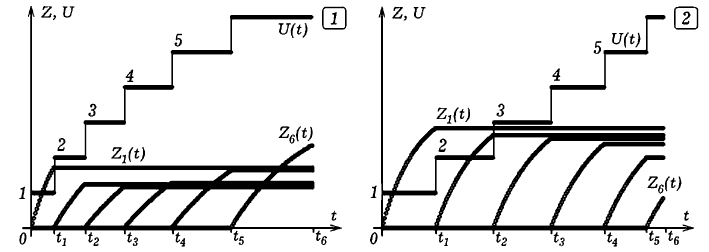
Рис. 3. Результаты оптимизации процесса обучения.

Рис. 3. Результаты оптимизации процесса обучения.

Задача 5.

Учащийся изучает N=6 темы, и по каждой из тем учитель может решить различное число задач. Время обучения ограничено, общее количество задач M=200. Коэффициент усвоения (i-1)-ой темы пропорционален уровню знаний предыдущей i-ой темы: a1= 0,04, a2= 0,04Z1, ai= 0,04Zi-1. Тест проверяет знания всех темы; коэффициенты важности равны: V1=V2=...=V5=1. Необходимо найти такое распределение задач, при котором результаты тестирования в конце обучения максимальны.

Результаты оптимизации представлены на рис. 3.2. Оценка за тест T=3,67 при Tmax=6.

Из результатов моделирования следует: 1. Если изучение i-ой темы приводит к увеличению коэффициента усвоения j-ой темы, то сначала следует изучать i-ую тему, а затем j-ую. 2. Если в выходном тесте в большей степени представлены задачи i-ой темы (то есть они имеют большую важность), то большую часть учебного времени следует решать задачи i-ой темы. Это приведет к более высоким результатам тестирования и повышению эффективности обучения.

Тексты программ находятся в zip-архиве, файл gl2-8.pas.

ВВЕРХ

Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс]. - Глазов: ГГПИ, 2012 // Web-site http://maier-rv.glazov.net .