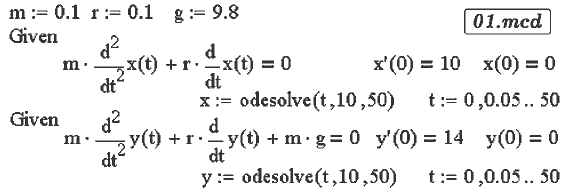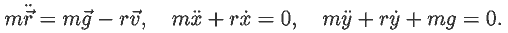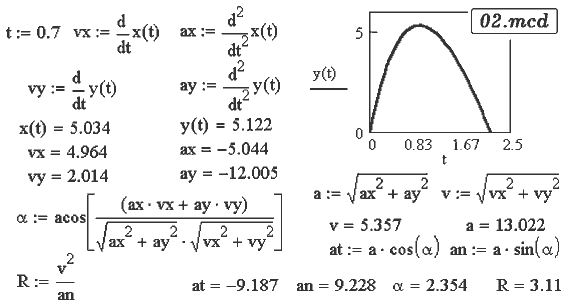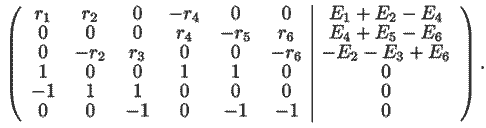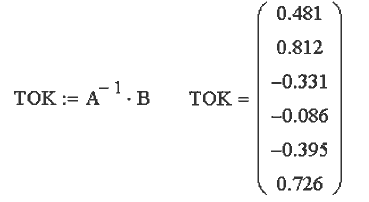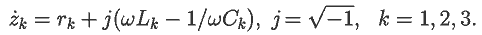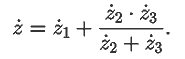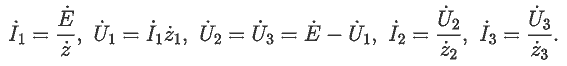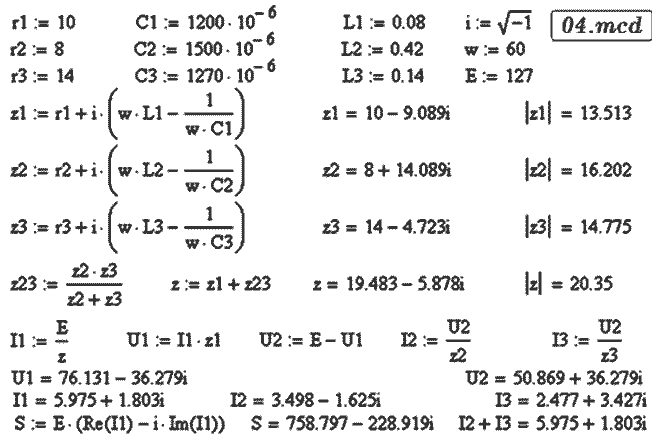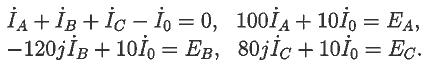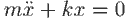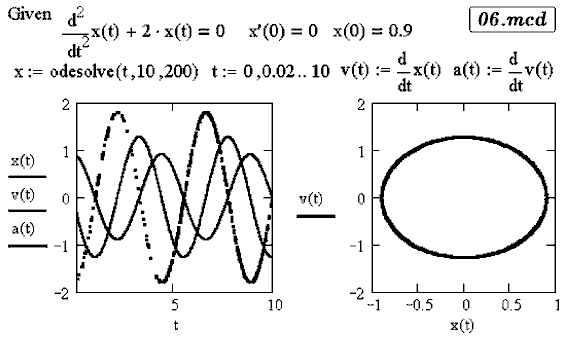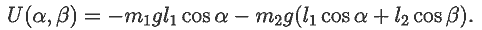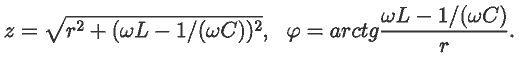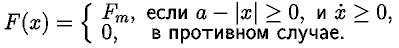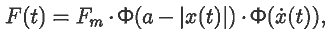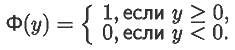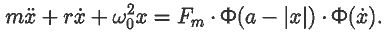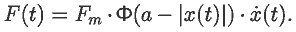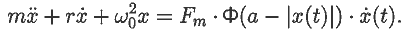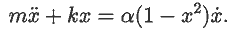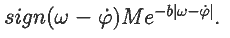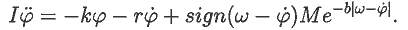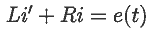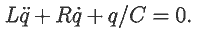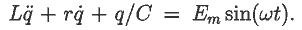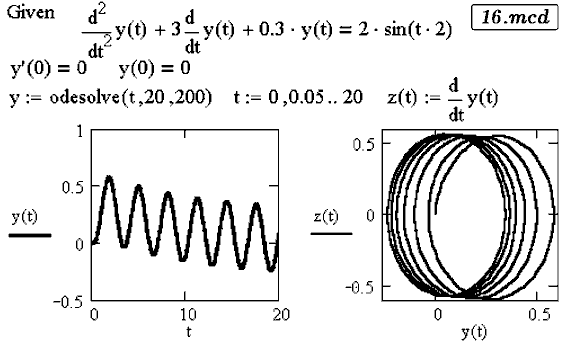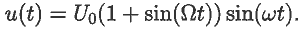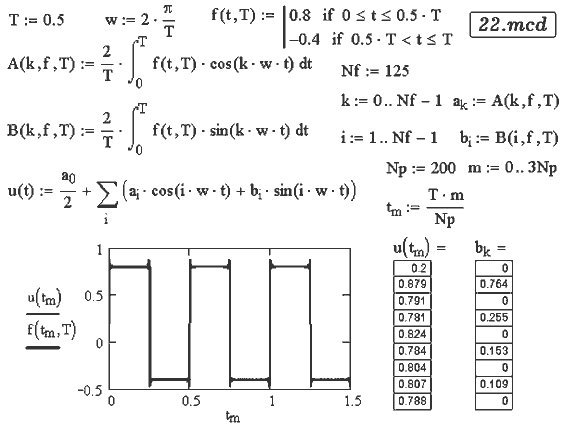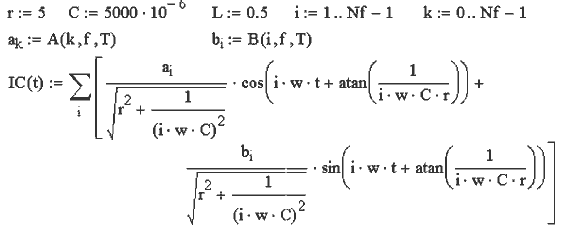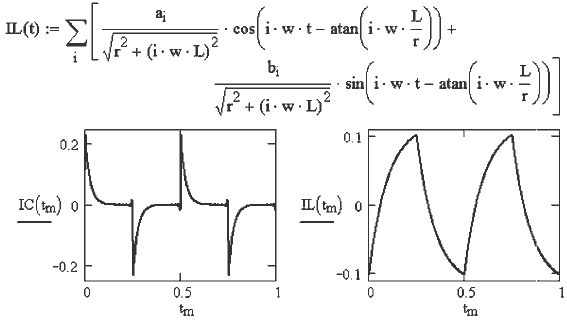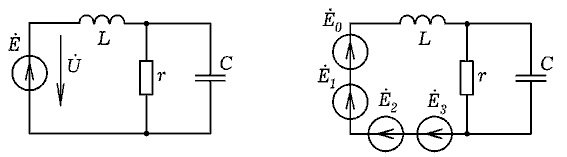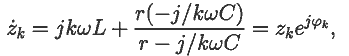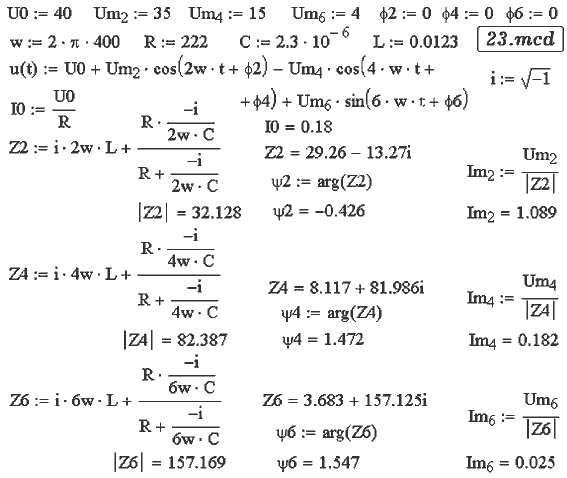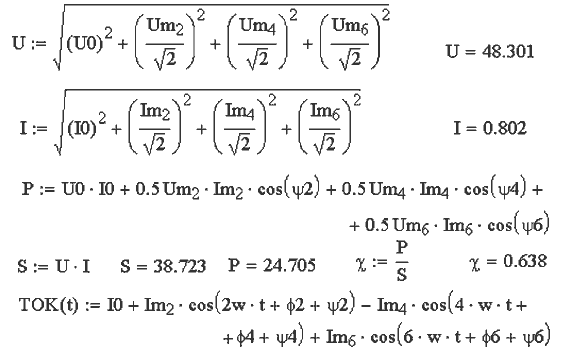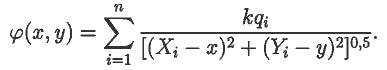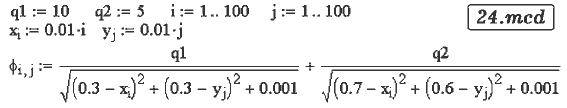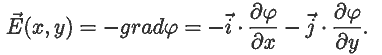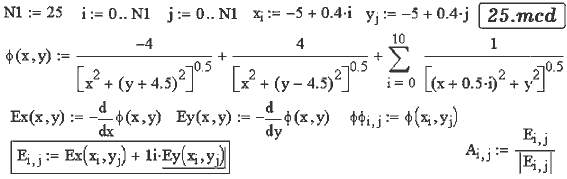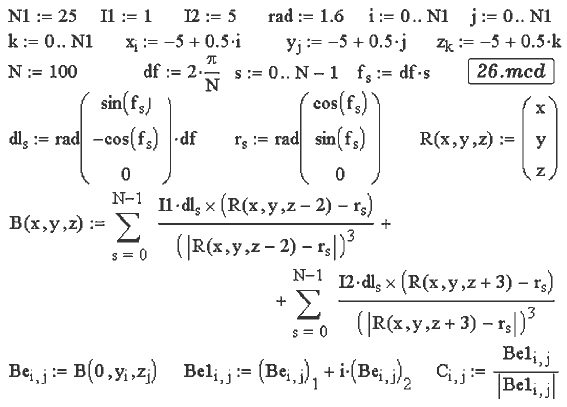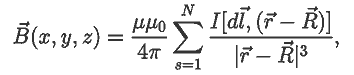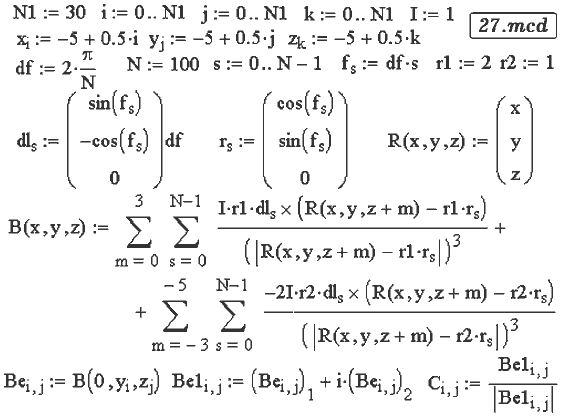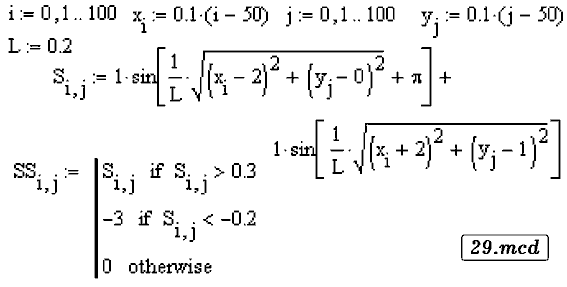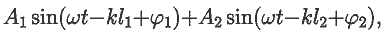ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования Глазовский государственный педагогический институт имени В.Г.Короленко . . Майер Р.В. РЕШЕНИЕ ФИЗИЧЕСКИХ ЗАДАЧ С ПОМОЩЬЮ ПАКЕТА MathCAD . . Глазов 2006

Майер, Р.В. Решение физических задач с помощью пакета MathCAD [Электронный ресурс] / Р.В.Майер. --- Глазов: ГГПИ, 2006. --- 37 c. В краткой форме рассмотрены некоторые способы решения физических задач с помощью математического пакета MathCAD. Показаны методы рассчета электрических цепей постоянного тока, однофазных и трехфазных цепей переменного тока, колебательных систем, переходных процессов, способы разложения функций в ряд Фурье и проведения спектрального анализа. Приведены примеры использования комплексных чисел, решения дифференциальных уравнений, построения графиков. Для студентов высших учебных заведений. СОДЕРЖАНИЕ 0. ПРЕДИСЛОВИЕ 1. ДВИЖЕНИЕ ТОЧКИ В ОДНОРОДНОМ ПОЛЕ С УЧЕТОМ СИЛЫ СОПРОТИВЛЕНИЯ 2. ЦЕПИ ПОСТОЯННОГО ТОКА 3. ОДНОФАЗНЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА 4. ТРЕХФАЗНЫЕ ЦЕПИ 5. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ 6. АВТОКОЛЕБАТЕЛЬНЫЕ ПРОЦЕССЫ 7. РЕЛАКСАЦИОННЫЕ ПРОЦЕССЫ 8. РАЗЛОЖЕНИЕ В РЯД ФУРЬЕ. СПЕКТРАЛЬНЫЙ АНАЛИЗ 9. ВЛИЯНИЕ ЕМКОСТИ И ИНДУКТИВНОСТИ НА КРИВУЮ ТОКА 10. РАСЧЕТ ЦЕПЕЙ, СОДЕРЖАЩИХ ИСТОЧНИК НЕГАРМОНИЧЕСКОЙ ЭДС 11. ЭЛЕКТРИЧЕСКОЕ И МАГНИТНОЕ ПОЛЕ 12. ИНТЕРФЕРЕНЦИЯ ВОЛН 13. МОДЕЛИРОВАНИЕ ЯВЛЕНИЙ ПЕРЕНОСА 14. ДИНАМИЧЕСКИЙ ХАОС ЛИТЕРАТУРА ПРИЛОЖЕНИЕ (цветные рисунки)

. ПРЕДИСЛОВИЕ Компьютерное моделирование, проведение вычислительного эксперимента является одним из современных методов исследования физических явлений. Он имеет свои особенности, преимущества и недостатки по сравнению с другими методами изучения физических систем. Совершенно очевидно, что студенты высших учебных заведений должны иметь представления о компьютерных моделях, численных методах изучения различных объектов познания, достаточно свободно ориентироваться в современных программных продуктах. Современный персональный компьютер позволяет за несколько секунд решить сложную систему уравнений, построить график изучаемой зависимости, промоделировать трудновоспроизводимый эксперимент. Важным уровнем овладения методами вычислительной математики и физики является самостоятельное написание студентами различных компьютерных программ на алгоритмических языках программирования Basic, Pascal, Visual Basic, Delphi. Создавая подобные компьютерные модели "с нуля", работая с исходным кодом программы, студент глубже понимает конкретные способы обработки информации, методы программирования. С другой стороны необходимо уметь работать с современными математическими пакетами, различными системами компьютерной математики. К ним относится пакет MathCAD --- достаточно распространенная система автоматического проектирования (САПР), в которой объединены редактор документов, системный интегратор, центр ресурсов, электронные книги, справочная система, броузер Интернета. Пакет MathCAD имеет мощный математический аппарат, позволяющий выполнять символьные вычисления, решать системы алгебраических и дифференциальных уравнений, операции с векторами и матрицами, писать программы, строить графики и поверхности, и т.д. Основы работы в MathCAD подробно изложены в соответствующей литературе и в настоящей работе не рассматриваются. В предлагаемом пособии проанализированы некоторые типы задач общего курса физики, которые могут быть решены средствами MathCAD и позволяют сформировать представления о возможностях использования этого математического пакета при изучении физики. ВВЕРХ

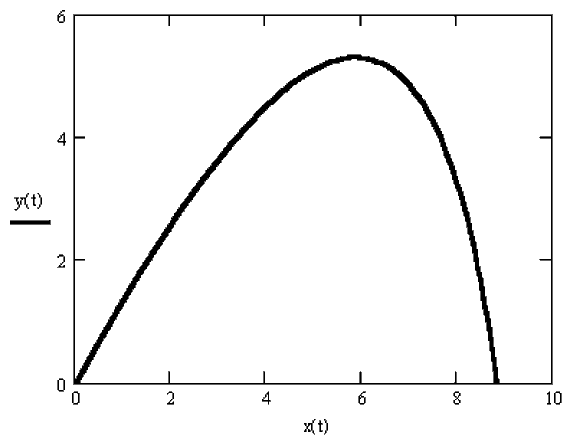
. 1. ДВИЖЕНИЕ ТОЧКИ В ОДНОРОДНОМ ПОЛЕ С УЧЕТОМ СИЛЫ СОПРОТИВЛЕНИЯ Задача 1. Тело бросили под углом к горизонту в однородном поле тяжести. Начальные координаты и скорость тела, коэффициент сопротивления воздуха известны. Напишите дифференциальные уравнения и построить траекторию движения тела. Из второго закона Ньютона: Решение этой системы уравнений --- в документе 01.mcd. Задача 2. Исследуйте движение тела в поле тяжести при других начальных условиях. Докажите, что из--за силы сопротивления воздуха время подъема меньше времени спуска на тот же уровень. Для этого достаточно проанализировать график y=y(t). Задача 3. Вычислите скорость и ее проекции на оси в данный момент времени времени. Найдите нормальное и тангенциальное ускорение, радиус кривизны траектории. Когда ускорение тела больше g? ВВЕРХ

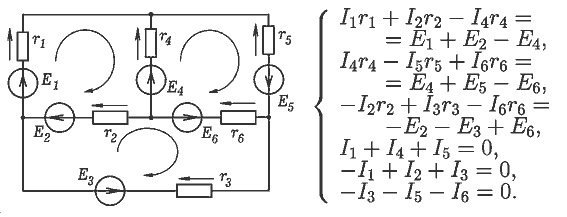
. 2. ЦЕПИ ПОСТОЯННОГО ТОКА Задача 5. Цепь состоит из нескольких ветвей, в каждой из которых находится источник ЭДС и резистор (рис.1). Необходимо рассчитать цепь, то есть определить токи во всех ее ветвях. Из законов Кирхгофа получаем систему уравнений: Для решения этой системы уравнений запишем матрицу: Левую часть матрицы, содержащую коэффициенты при токах Ii, обозначим через A, а правую --- через B. Чтобы получить матрицу токов в MathCAD используется оператор TOK:=A-1 · B. Решение задачи представлено в документе 03.mcd. Задача 6. Рассчитайте цепь, состоящую из нескольких источников ЭДС и резисторов, и составьте баланс мощностей. ВВЕРХ

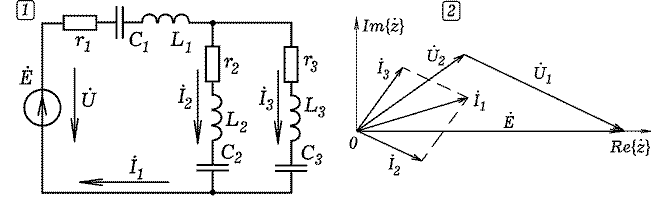
. 3. ОДНОФАЗНЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА Задача 7. Цепь состоит из источника переменной ЭДС и трех ветвей, в каждой из которых резистор, конденсатор и катушка индуктивности. Вторая и третья ветви соединены параллельно между собой, последовательно с ними включена первая ветвь. Рассчитайте все токи и напряжения, полную, активную и реактивную мощности. Постройте векторную диаграмму. Определите действующие значения всех токов и напряжений. Импеданс k--ой ветви, содержащей последовательно соединенные резистор rk, конденсатор Ck и катушку индуктивности Lk, равен: Если ветви 2 и 3 соединены параллельно, а ветвь 1 --- последовательно с ними, то импеданс цепи: Неизвестные токи и напряжения найдем из закона Ома: Это позволяет построить векторную диаграмму цепи, рассчитать комплекс полной мощности. Решение задачи представлено в файле 04.mcd. Задача 8. Добавьте к предыдущей цепи четвертую ветвь параллельно источнику. Величины сопротивления, емкости и индуктивности подберите сами. Рассчитайте цепь, постройте векторную диаграмму. Задача 9. Решите задачу 7 для случая, когда первая и третья ветви состоят их резистора, конденсатора и катушки индуктивности, соединенных параллельно. Постройте векторную диаграмму. ВВЕРХ

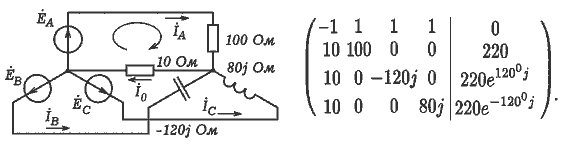
. 4. ТРЕХФАЗНЫЕ ЦЕПИ Задача 10. Имеется четырехпроводная трехфазная цепь с несимметричной нагрузкой. Определите комплексы токов во всех линейных и нейтральном проводах, их модули, вычислите мощность, постройте векторные диаграммы. Из законов Кирхгофа получаем систему: Для ее решения создают две матрицы A и B, затем получают третью матрицу TOK:=A-1· B, элементами которой являются комплексы токов (документ 05.mcd). Их модули равны действующим значениям токов. Задача 11. Рассчитайте четырехпроводную трехфазную цепь с несимметричной нагрузкой, каждая фаза которой содержит резистор, конденсатор, катушку индуктивности, соединенные смешанно. Задача 12. Рассчитайте трехфазную цепь с несимметричной нагрузкой, соединенной треугольником. Каждая фаза нагрузки содержит резистор, конденсатор, катушку индуктивности, соединенные смешанно. Задача 13. Фазоуказатель состоит из конденсатора и двух одинаковых лампочек, соединенных звездой без нейтрали. Какая из лампочек будет гореть ярче, если конденсатор находится в фазе A? ВВЕРХ

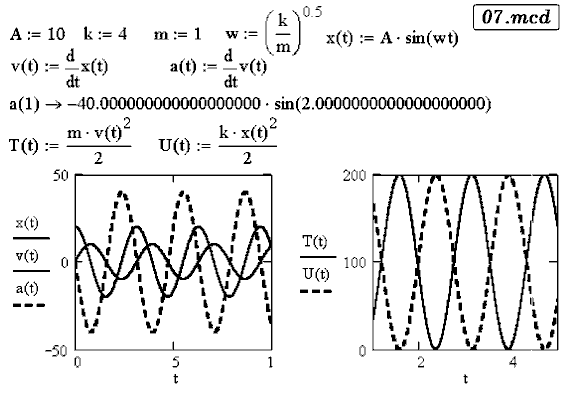
. 5. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ Задача 14. Имеется идеальная колебательная система. Ее вывели из состояния равновесия и предоставили самой себе. Получите график колебательного движения и фазовую кривую. Решение дифференциального уравнения незатухающих колебаний: представлено в документе 06.mcd. Задача 15. Тело, подвешенное на пружине, совершает гармонические колебания x(t)=Asin(ωt+φ). Средствами MathCAD продифференцируйте эту зависимость, постройте графики зависимости кинетической и потенциальной энергии от времени (07.mcd). Задача 16. Двойной маятник состоит из подвешенной на нити длиной L1 материальной точки m1, к которой с помощью нити длиной L2 подвешена материальная точка m2. Изучите зависимость потенциальной энергии от углов α и β, которые образуют нити с вертикалью. 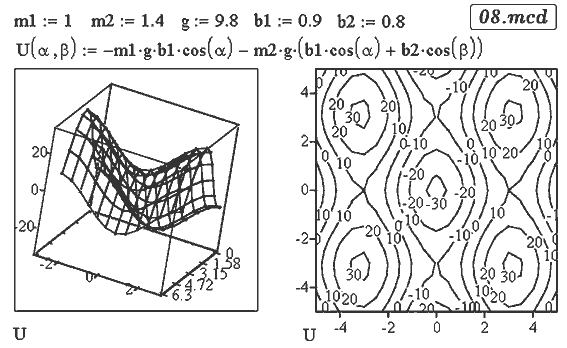Маятник движется в одной вертикальной плоскости, система имеет две степени свободы. Ее потенциальная энергия равна: В файле 08.mcd построена поверхность U=U(α,β), характеризующая зависимость потенциальной энергии от координат маятника. Видно, что значениям α=π и β=0 соответствует седлообразное положение равновесия: потенциальная энергия по координате α достигает максимума, а по координате β --- минимума. 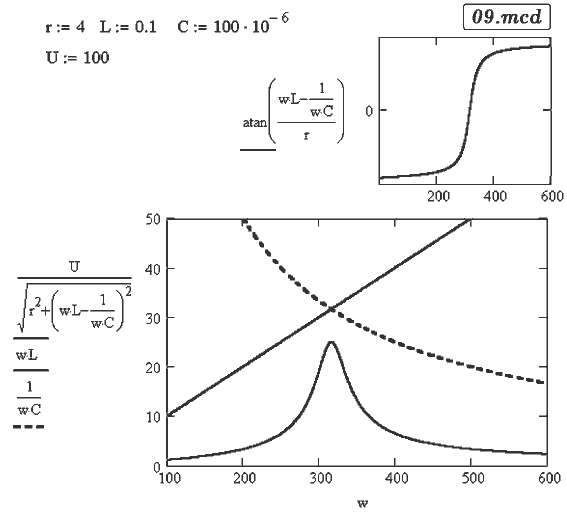Задача 17. Последовательный колебательный контур, состоящий из резистора, конденсатора и катушки индуктивности, подключен к источнику переменного напряжения регулируемой частоты. Постройте график зависимости тока, напряжения на конденсаторе и катушке индуктивности, сдвига колебаниями тока и напряжения питания от частоты. Полное сопротивление колебательного контура и сдвиг фаз между колебаниями тока и напряжения: Ток в контуре равен I=U/z. Решение задачи --- в документе 09.mcd. ВВЕРХ

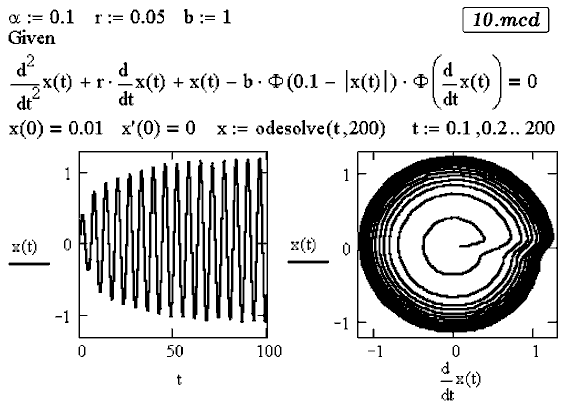
. 6. АВТОКОЛЕБАТЕЛЬНЫЕ ПРОЦЕССЫ Задача 18. Исследуйте автоколебательную систему, в которой один раз за период осциллятору сообщается энергия (действует постоянная сила). Постройте график колебаний и фазовую траекторию. Рассмотрим колебательную систему, на которую при смещениях x в интервале [-a; a] и движении в положительном направлении действует постоянная сила, равная Fm: Силу запишем иначе: В этом случае уравнение автоколебаний принимает вид: Соответствующий документ MathCAD представлен в файле 10.mcd. На фазовой кривой хорошо виден скачок, соответствующий увеличению амплитуды колебаний при передаче колебательной системе очередной порции энергии. Множество точек, к которому стремится фазовая кривая называется аттрактором. Задача 19. Промоделируйте движение автоколебательной системы, в которой каждый раз при прохождении положения равновесия (дважды за период) осциллятору сообщается энергия (действует постоянная сила). 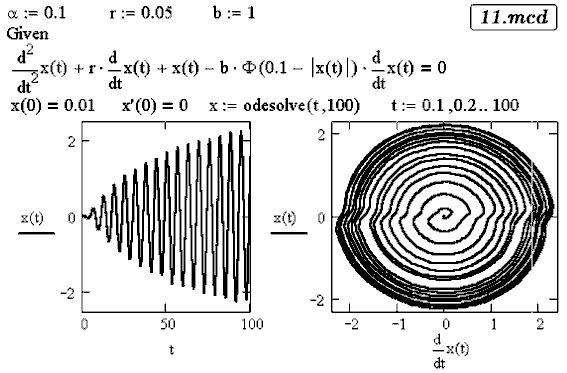Пусть система подталкивает осциллятор вблизи положения равновесия, действуя на него с постоянной силой b: Из второго закона Ньютона получаем дифференциальное уравнение: Решение этого уравнения представлено в файле 11.mcd. 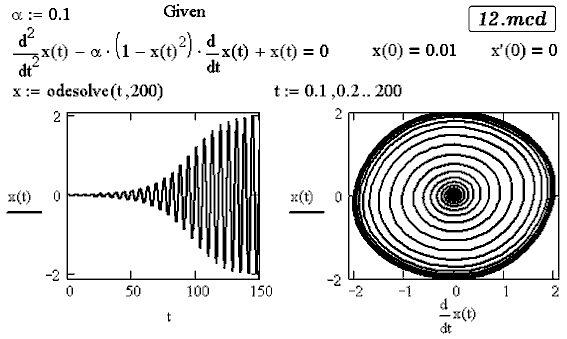Задача 20. Промоделируйте автоколебательную систему, описывающуюся уравнением Ван-дер-Поля: Решение задачи приведено в документе 12.mcd. Колебательная система воздействует посредством положительной обратной связи на клапан, регулирующий поступление энергии от источника, в результате чего возникают автоколебания. Их амплитуда растет до тех пор, пока энергия потерь за период не будет равна энергии от источника. 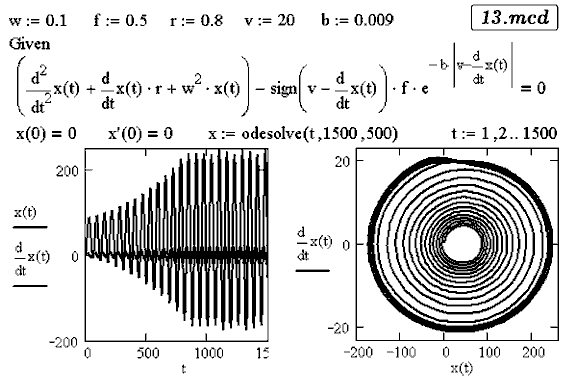Задача 21. Фрикционный маятник Фроуда состоит из физического маятника, расположенного на вращающемся валу. Сила трения между валом и маятником с увеличением их относительной скорости убывает. Исследуйте колебания маятника. Проекцию вращающего момента, действующего со стороны вала на маятник, будем считать равной Если маятник движется в направлении вращения и его скорость меньше скорости вала, то со стороны вала на него действует достаточно большой момент силы трения в направлении вращения вала. Когда маятник движется в противоположном направлении, его скорость относительно вала велика, поэтому момент силы трения мал. Так автоколебательная система регулирует поступление энергии к осциллятору. Запишем второй закон Ньютона в проекциях: Для решения этого дифференциального уравнения используется документ 13.mcd. Из графиков x=x(t) и v=v(t) видно, что маятник Фроуда колеблется относительно нового положения равновесия, смещенного в сторону вращения вала, причем его скорость в установившемся режиме не превышает скорость вала ω. Замкнутая кривая на фазовой плоскости, при t стремящемся к бесконечности является аттрактором. Задача 22. Промоделируйте движения маятника Фроуда для случая, когда начальная скорость маятника превышает скорость вращения вала. Убедитесь, что через достаточно большой промежуток времени система переходит в установившееся состояние, фазовая кривая стремиться к аттрактору. ВВЕРХ

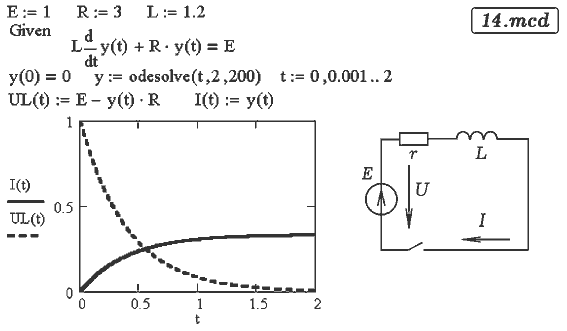
. 7. РЕЛАКСАЦИОННЫЕ ПРОЦЕССЫ Задача 23. Цепь состоит из резистора и катушки индуктивности, подключаемых к источнику постоянного напряжения. В начальный момент ток через катушку равен 0. Определите значение тока и напряжения на катушке в последующие моменты времени. Решение дифференциального уравнения переходного процесса представлено в документе 14.mcd. Задача 24. Колебательный контур содержит резистор, конденсатор, катушку индуктивности. Конденсатор зарядили и подключили к цепи. 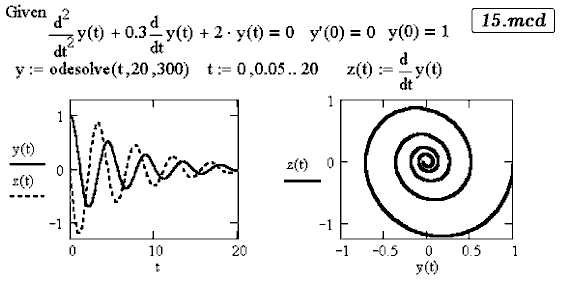Исследуйте получающиеся затухающие колебания. Дифференциальное уравнение затухающих колебаний выглядит так: Его решение представлено в документе 15.mcd. Задача 25. Исследуйте цепь из резистора, конденсатора и катушки индуктивности, подключаемых к источнику переменного напряжения. В начальный момент конденсатор разряжен, ток через катушку индуктивности равен 0. Запишем дифференциальное уравнение переходного процесса: Начальные условия: q(0)=Cu(0)=0, i(0)=q'(0)=0. Решение этого уравнения представлено в документе 16.mcd. ВВЕРХ

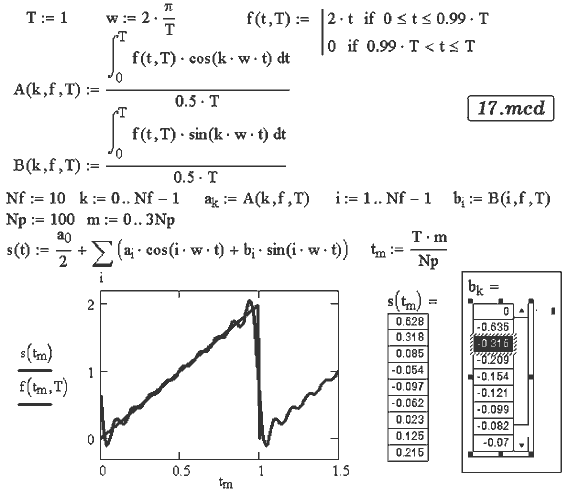
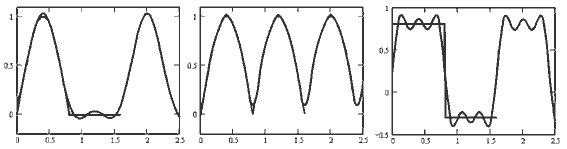
. 8. РАЗЛОЖЕНИЕ В РЯД ФУРЬЕ. СПЕКТРАЛЬНЫЙ АНАЛИЗ Задача 26. Разложите пилообразные импульсы напряжения u(t) в ряд Фурье. Восстановите сигнал по 3, 7, 15, 30 и 50 первым гармоникам. Сравните получившуюся функцию с исходной. Решение задачи предложено в документе 17.mcd. Задача 27. Разложите импульсы, получающиеся в результате однополупериодного и двухполупериодного выпрямления, в ряд Фурье. Восстановите сигнал по 3, 7, 15, 30 и 50 первым гармоникам. 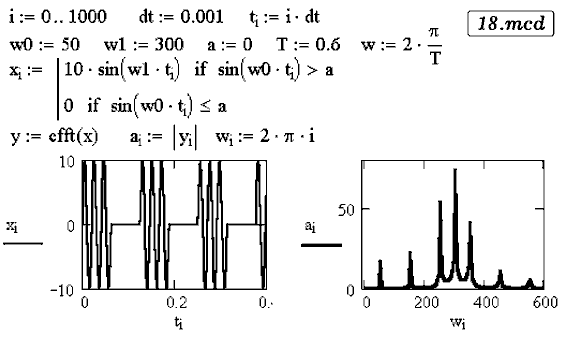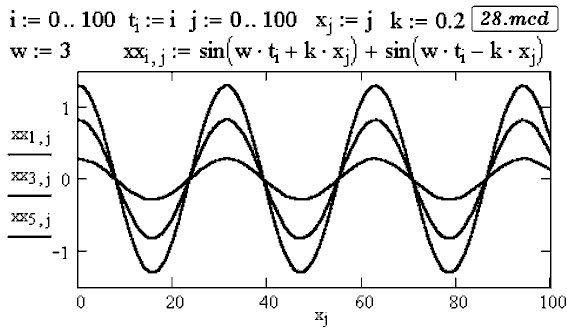Задача 28. Получите спектр последовательности радиоимпульсов, представляющих собой обрывки синусоидальных колебаний. Решение --- в документе 18.mcd. 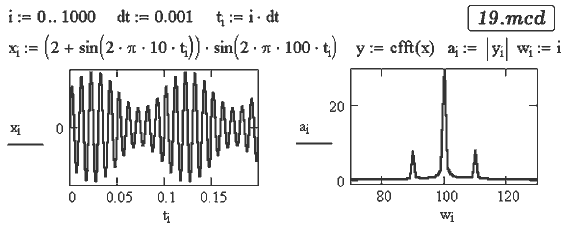Задача 29. Получите спектр амплитудно--модулированного сигнала Видно, что спектр содержит колебания на основной частоте и на двух зеркальных частотах (документ 19.mcd). 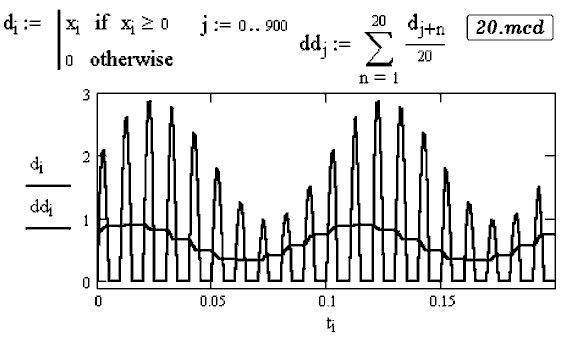Задача 30. Доработайте программу так, чтобы промоделировать детектирование амплитудно--модулированного сигнала. Детектором является диод, обрезающий нижнюю часть синусоиды, а сглаживание пульсаций осуществляется за счет емкостного фильтра (документ 20.mcd). 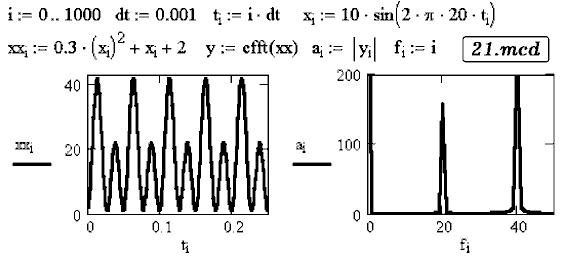Задача 31. Характеристика нелинейного элемента может быть аппроксимирована полиномом второй степени i(u)=au2+bu+c. Изучите спектральный состав отклика системы (силы тока) на оказываемое гармоническое воздействие (напряжение) (документ 21.mcd). ВВЕРХ

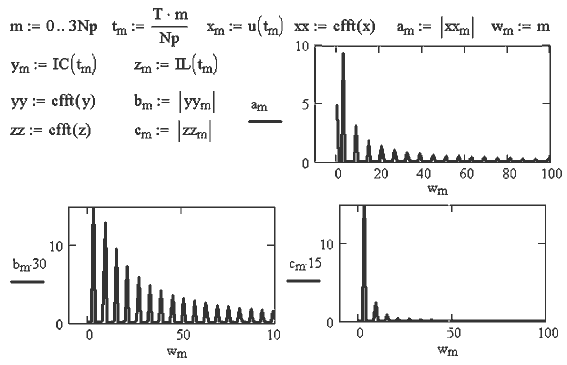
. 9. ВЛИЯНИЕ ЕМКОСТИ И ИНДУКТИВНОСТИ НА КРИВУЮ ТОКА Задача 32. К источнику периодической негармонической ЭДС подключена активно--емкостная (активно--индуктивная) нагрузка. Используя разложение в ряд Фурье, получите кривые тока и изучите их спектр. При активно--индуктивной нагрузке кривая тока в большей степени похожа на синусоиду, чем кривая напряжения, а в случае активно--емкостной --- наоборот (документ 22.mcd). Это объясняется тем, что гармоникам тока высокого порядка конденсатор оказывает меньшее сопротивление, а катушка индуктивности --- большее. ВВЕРХ

. 10. РАСЧЕТ ЦЕПЕЙ, СОДЕРЖАЩИХ ИСТОЧНИК НЕГАРМОНИЧЕСКОЙ ЭДС Задача 33. Цепь состоит из параллельно соединенных резистора и конденсатора, к которым последовательно подключена катушка индуктивности и источник негармонического напряжения u(t)=U0+Um1sin(ωt+φ1)+ Um2sin(2ω t+φ2)+ Um3sin (3ω t+φ3). Найдите токи в ветвях, их действующие значения, мощности. Заменим этот источник источником постоянной ЭДС U0 и тремя источниками переменной ЭДС Um1sin(ωt+φ1), Um2sin(2ωt+φ2), Um3sin(3ωt+φ3). Найдем импеданс цепи для k-ой гармоники: где tg(φk) равен отношению мнимой и действительной частей импеданса. 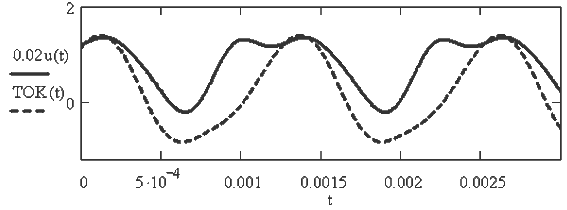Комплексная амплитуда k--ой гармоники тока определяется как отношение комплексной амплитуды напряжения к импедансу для k--ой гармоники. В представленном ниже документе MathCAD (23.mcd) построен график u(t), рассчитаны импедансы и амплитуды токов для различных гармоник, найдены действующие значения тока и напряжения, определена зависимость i(t), построен график. ВВЕРХ

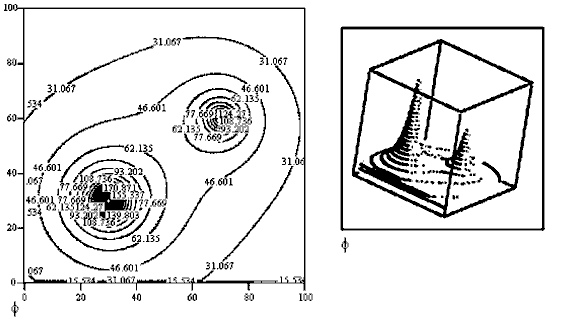
. 11. ЭЛЕКТРИЧЕСКОЕ И МАГНИТНОЕ ПОЛЕ Задача 34. Два точечных электрических заряда q1, q2 имеют координаты (X1,Y1) и (X2,Y2). Рассчитайте распределение потенциала электрического поля, постройте эквипотенциальные линии и поверхность φ=φ(x,y). Потенциал электрического поля, создаваемого зарядами qi с координатами (Xi,Yi), i=1, 2, ... в точке (x,y) равен: Результаты расчета эквипотенциальных линий и поверхности φ=φ(x,y) --- в документе 24.mcd. Заряды положительные, поэтому по мере приближения к каждому из них потенциал возрастает. 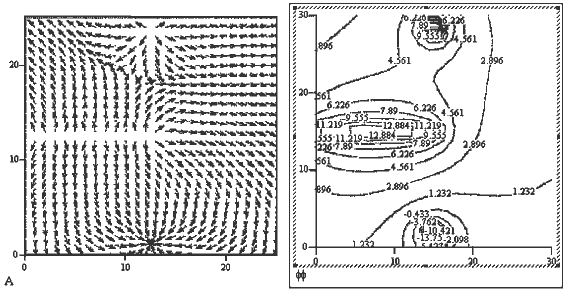Задача 35. Рядом с заряженной пластиной расположены два точечных заряда. Изучите распределение потенциала и постройте силовые линии напряженности электрического поля. Зависимость φ=φ(x,y) определяется как в предыдущей задаче, напряженность электрического поля в двумерном случае равна: Для построения силовых линий вычисляются проекции вектора напряженности на оси координат и создается матрица Ei,j:=Ex(xi,yj)+ 1i· Ey(xi,yj) и нормированная матрица Ai,j, используемая для построения векторного поля (25.mcd). Задача 36. Рассчитайте индукцию магнитного поля, создаваемого двумя витками с током, и постройте силовые линии в случаях, когда токи сонаправлены и противоположно направлены. 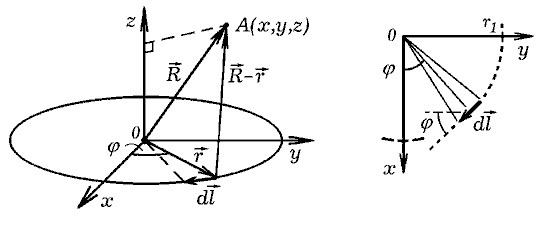Рассмотрим виток с током, лежащий в плоскости XOY, с центром в точке O. Разобъем его на элементы dls, определим элементарный магнитный момент, создаваемый каждым элементом в точке наблюдения, и просуммируем их. Элемент витка и точка наблюдения имеют координаты (r·cosφs, r·sinφs, 0), и (x, y, z) соответственно. Для расчета индукции магнитного поля используется закон Био--Савара--Лапласа: где μ0 --- магнитная постоянная, I --- сила тока. 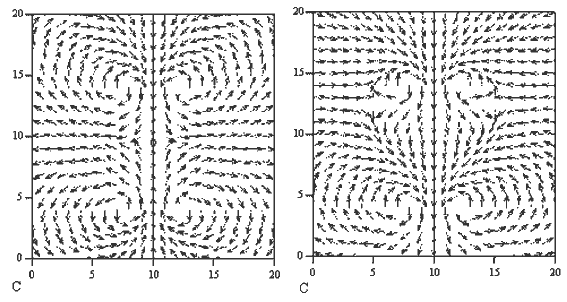Решение приведено в документе 26.mcd. Витки расположены параллельно плоскости XOY, на экране получаются силовые линии магнитного поля в плоскости YOZ. Задача 37. В рассмотренном случае постройте график зависимости модуля индукции магнитного поля от координаты вдоль оси витков с током и перпендикулярно ей. Задача 38. Получите проекции вектора индукции магнитного поля на плоскость перпендикулярную оси соленоида (витка) с током. Задача 39. Рассчитайте магнитное поле, создаваемое двумя (тремя) параллельными проводниками, по которым текут токи в различных направлениях. Задача 40. Изучите магнитное поле, создаваемое соленоидом и прямолинейным проводником с током. Получите проекции индукции магнитного поля на плоскость, содержащую проводник с током. 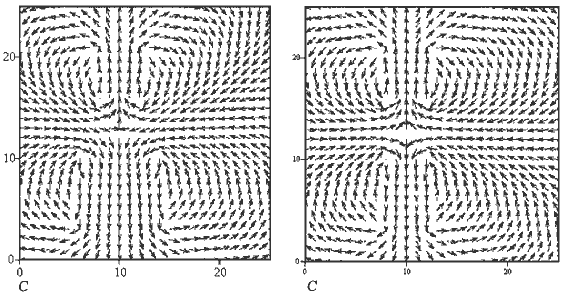Задача 41. Имеется два соленоида, расположенных соосно по отношению друг к другу. Постройте силовые линии магнитного поля в случаях, когда токи текут в одном направлении и в противоположных направлениях (27.mcd). ВВЕРХ

. 12. ИНТЕРФЕРЕНЦИЯ ВОЛН Задача 42. Две волны с равными частотами распространяются навстречу друг другу. В результате их наложения возникает стоячая волна. Постройте смещения частиц среды в различные моменты времени (28.mcd). Задача 43. Рассчитайте интерференционную картину, создаваемую двумя когерентными источниками, работающими в противофазе, в плоскости, содержащей эти источники. Расстояние от источников до точки наблюдения равно: где a, b задают смещение второго источника относительно первого. Pезультирующее колебание в точке наблюдения находится как сумма где k=2π/λ --- волновое число. Решение --- в файле 29.mcd. Задача 44. Рассчитайте интерференционную картину от двух источников, на плоскости, расположенной параллельно прямой, содержащей эти источники. Длина волны и расположение источников известны. Геометрическая разность хода и интенсивность равны: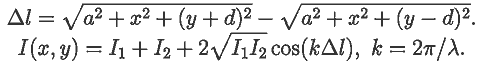 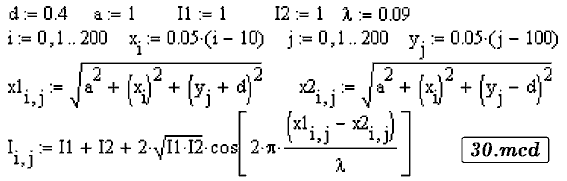Решение задачи представлено в документе 30.mcd. ВВЕРХ

. 13. МОДЕЛИРОВАНИЕ ЯВЛЕНИЙ ПЕРЕНОСА Задача 45. Однородный стержень с известным коэффициентом температуропроводности нагревают в середине. Правый конец поддерживается при постоянной температуре, левый --- теплоизолирован. Начальное распределение температуры и мощность источника известны. Определите температуру в последующие моменты времени. 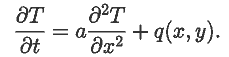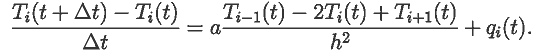Уравнение теплопроводности для стержня: В конечных разностях получаем: Решение задачи в документе 31.mcd. В результате вычислений получаются кривые T=T(t,x) зависимости температуры от координаты x в заданные моменты времени t. Видно, что температура средней части стержня за счет источников тепла повышается. 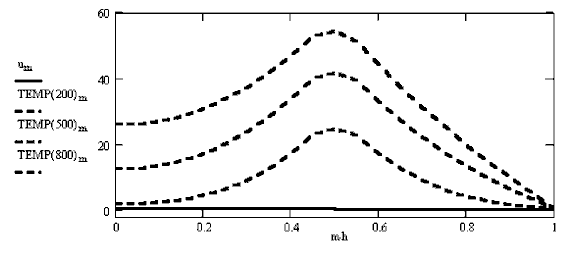Моделирование диффузии осуществляется аналогично. Задача 46. Стержень разрезали на две половины и одну из них нагрели, после чего половинки стержня соединили. Рассчитайте распределение температуры вдоль стержня в последующие моменты времени. Задача 47. Часть сосуда заполнена водным раствором соли, а другая часть --- чистой водой. Изучите самопроизвольное перемешивание жидкостей за счет диффузии. 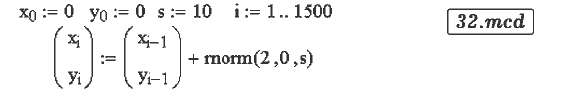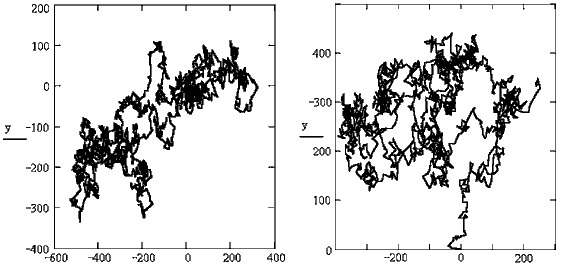ВВЕРХ

. 14. ДИНАМИЧЕСКИЙ ХАОС Задача 48. Промоделируйте хаотическое движение броуновской частицы. На броуновскую частицу со стороны окружающих ее молекул действует сила, хаотическим образом изменяющая свою величину и направление. Чтобы промоделировать ее движение необходимо прибавлять к координатам частицы случайные величины (документ 32.mcd). Траектория частицы является фракталом, то есть объектом, любая часть которого после увеличения подобна целому. 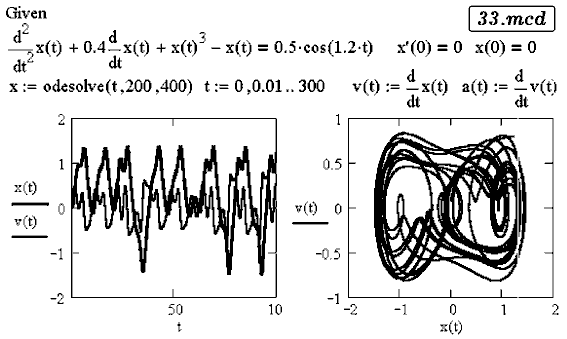Задача 49. Колебательная система состоит из шарика, находящегося внутри потенциальной ямы с двумя углублениями, задаваемой функцией: U(x)=0.25x4-0.5x2. 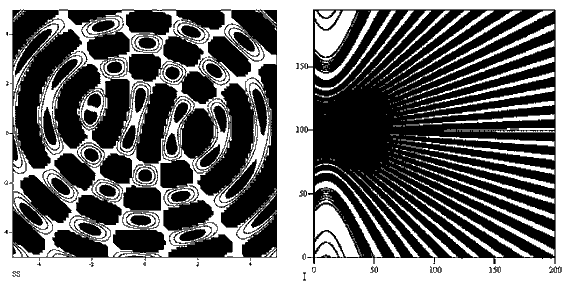На шарик действует вынуждающая сила F(t)=Fmcos(ω t). Исследуйте поведение системы. Потенциальное поле создает возвращающую силу 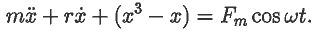Из второго закона Ньютона получаем дифференциальное уравнение колебаний: Два варианта решения представлены в документах 33.mcd и 34.mcd. Видно, что система совершает хаотические колебания относительно двух положений равновесия. 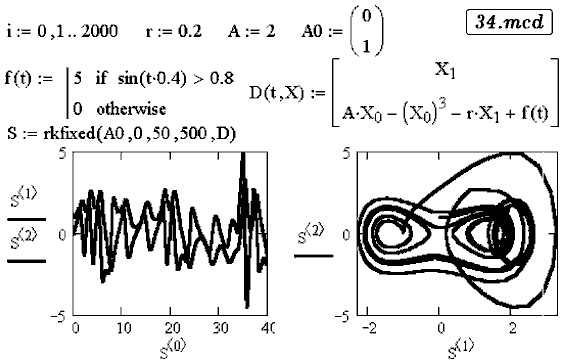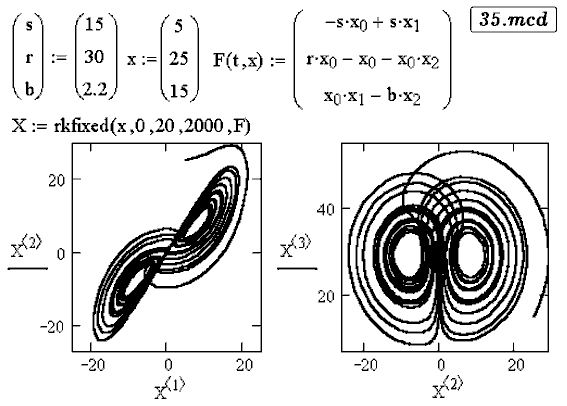Задача 50. Конвекционные потоки в атмосфере описываются системой дифференциальных уравнений dx/dt=a(-x+y), dy/dt=bx-y-xz, dz/dt=-cz+xy. Изучите поведение этой системы, получите странный аттрактор Лоренца. В чем состоит эффект бабочки? Решение задачи --- в документе 35.mcd. Видно, что аттрактор Лоренца похож на закрученную восьмерку, и захватывает две большие области фазового пространства. При этом малые изменения состояния атмосферы могут привести к существенным изменениям ее состояния в будущем. Например, бабочка, взмахнув крыльями в Австралии, при определенных метеорологических условиях может вызвать торнадо в Америке. 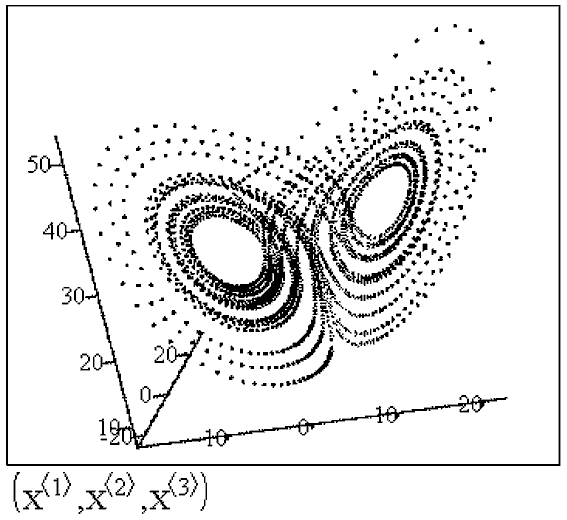ВВЕРХ

Внедрение в учебный процесс компьютерной техники позволяет существенным образом изменить методику изучения некоторых вопросов курса физики, связанных с осуществлением громоздких, многократно повторяющихся вычислительных процедур, решением систем дифференциальных уравнений, построением графиков и поверхностей, наглядным представлением результатов решения задачи. Если раньше поведение физической системы анализировалось исключительно аналитически, то теперь появилась возможность применения численных методов компьютерного моделирования, что имеет определенные преимущества. Рассмотренные выше задачи создают лишь общее представление о возможностях пакета MathCAD. Более глубокое изучение вопроса требует привлечения специальных руководств и пособий, некоторые из которых перечислены в списке литературы. Настоящее электронное пособие может быть использовано студентами и преподавателями при изучении основ компьютерного моделирования, методов математической физики, а также при решении задач курсов общей физики, электротехники и т.д. ВВЕРХ

. ЛИТЕРАТУРА Дьяконов, В. MathCAD 2000 [Текст]: учебный курс / В.Дьяконов --- СПб.: Питер, 2001. --- 592 с. Кирьянов, Д.В. MathCAD 12 [Текст]: наиболее полное руководство / Д.В.Кирьянов. --- Спб. БХВ -- Петербург, 2005. --- 562. Майер, Р.В. Информационные технологии и физическое образование [Текст] / Р.В.Майер. --- Глазов: ГГПИ, 2006. --- 64 с. Поршнев, С.В. Компьютерное моделирование физических процессов с использованием пакета MathCAD [Текст]: учебное пособие / С.В.Поршнев. --- М.: Горячая линия--Телеком, 2002. --- 252 c. Физическая энциклопедия / Гл. ред. А.М.Прохоров. Ред. кол. Д.М.Алексеев, А.М.Балдин, А.М.Бонч-Бруевич, А.С.Боровик--Романов и др. --- М.: Большая Российская энциклопедия. --- 1992--1995. (в 6 томах). ПРИЛОЖЕНИЕ Автор: МАЙЕР Роберт Валерьевич, доктор педагогических наук, профессор кафедры информационных технологий в физическом образовании физического факультета Глазовского государственного педагогического института. Издательская лицензия ИД N06035 от 12.10.2001. Формат 60 x 90 1/16. Усл. печ. л. 2,15. Глазовский государственный педагогический институт. 427621, Удмуртия, г. Глазов, ул. Первомайская, 25. ВВЕРХ