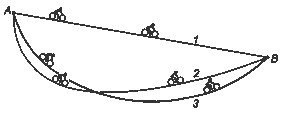
Представьте себе две произвольные точки A и B в поле тяжести Земли (рис.1). Их можно соединить бесконечно большим числом кривых 1, 2, 3 и т.д. Допустим, что каждая кривая является горкой, по которой под действием силы тяжести движется отпущенное в точке A без начальной скорости тело, например, не крутя педали, скатывается велосипедист или скользит лыжник. Понятно, что затрачиваемое время движения из A в B зависит от траектории движения и, видимо, существуют такая траектория, для которой оно минимально. На первый взгляд кажется, что быстрее всего из точки A в точку B можно скатиться по прямолинейной горке. Однако, это не так: иследования показали, что существует такая кривая 3, время спуска по которой минимально. Это кривая наикратчайшего спуска называется брахистохроной: brachistos --- кратчайший + chonos ---время. Оказывается брахистохроной является циклоида --- кривая, описываемая точкой окружности, без проскальзывания катящейся по прямой.

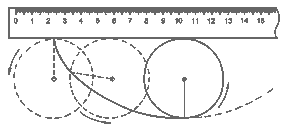
Циклоидальная кривая обладает еще одним замечательным свойством: если два тела одновременно отпустить без начальной скорости в разных точках циклоидальной горки, то они достигнут ее нижней точки также одновременно. За это циклоиду называют таутохроной: tauto --- тот же самый + chronos --- время, то есть равновременной кривой, время движения по которой не зависит от точки запуска.

Если вы хотите убедиться в брахистохронных и таутохронных свойствах циклоиды, то необходимо построить эту кривую. Для этого из картона вырежьте круг диаметром 80 мм, на краю которого поставьте метку. На лист плотной бумаги положите линейку и придвиньте к ней круг так, чтобы метка касалась линейки (рис. 2; для наглядности на круге проведен радиус, конец которого и является меткой). Карандашом на бумаге поставьте точку рядом с меткой и без проскальзываения катите круг по линейке, отмечая на листе последовательные положения метки. Продолжайте до тех пор, пока круг не совершит полный оборот, затем соедините обозначенные точки плавной кривой --- вы получите арку циклоиды. Аккуратно прорежьте бумагу вдоль построенной линии --- получившийся шаблон пригодиться в дальнейшем для изготовления циклоидальной направляющих.

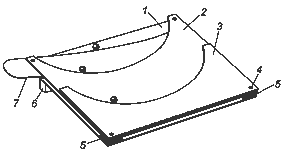
Основная сложность непосредственного наблюдения брахистохронных и таутохронных свойств циклоиды состоит в том, что время движения по циклоидальной горке разумных размеров слишком мало, чтобы визуально заметить одновременность или отставание одного из шариков. Увеличить время движения шариков, не увеличивая размеров траектории, можно, "уменьшив ускорение свободного падения". Для этого достаточно повернуть плоскость циклоиды вокруг горизонтальной оси так, чтобы она составила небольшой угол с горизонталью. В этом случае сущность явления не изменится, однако роль ускорения свободного падения будет играть его проекция на плоскость циклоиды.

На рис. 3 изображен эскиз прибора, позволяющего убедиться в брахистохронности и таутохронности циклоиды. На поверхности стола с помощью подставки 6 под углом 5--15 градусов установлена прямоугольная пластина 1 размером 2×200×280 мм, вырезанная из пластика или дюраля. На ней через прокладки 5 посредством винтов 4 закреплена пластина 2, верхняя кромка которой представляет собой арку циклоиды, вырезанную лобзиком по изготовленному как описано выше шаблону. К пластине 2 прикреплена циклоидальная пластина 3, верхняя кромка которой идентична верхней кромке пластины 2, то есть имеет форму арки циклоиды тех же размеров. Верхние кромки пластин 2 и 3 расположены точно друг под другом. В зазоре между пластинами 1 и 2, с возможностью поворота вокруг винта 4 в левом верхнем углу прибора, установлена пластина 7, верхняя кромка которой имеет вид произвольной кривой или просто прямолинейна. Выступающая за габариты прибора часть направляющей пластины 7, играет роль рукоятки для установки пластины в нужное положение. Для проведения опытов необходимы два одинаковых стальных шарика диаметром 7--9 мм. Допустимо использование более толстых пластин, шариков с большим диаметром, пропорциональные изменения всех размеров прибора.

Если шарики установить на нециклоидальную и циклоидальную направляющие (верхние кромки пластин 7 и 2) в левом верхнем углу прибора и одновременно отпустить, то второй шарик опережает первый, двигающийся по нециклоидальной траектории, и раньше достигает нижней точки пересечения двух направляющих, где и проваливается на пластину 1. После остановки шариков видна поледовательность их расположения по правой на рисунку части циклоидальной траектории, совпадающая с последовательностью их прихода в указанную точку. Если повернуть нециклоидальную направляющую или заменить ее на другую, то результат опыта не изменится.

Таутохронность циклоиды вы можете пронаблюдать так. Шарики установите в произвольных точках верхних кромок циклоидальных направляющих и одновременно отпустите. Вы увидете, что скатываясь по направляющим, шарики, независимо от точек запуска достигают нижних точек циклоидальных траекторий одновременно, затем, проскочив их по инерции, одновременно останавливаются в верхних точках своих траекторий, возвращаются назад и т.д. Иными словами, шарики cовершает синфазные колебания с разными амплитудами, но равными периодами, что и доказывает таутохронность циклоиды.

Демонстрационный прибор состоит из кодоскопа, прозрачного планшета, и магнитных ловушек для стальных шариков. В планшете прорезаны одна прямая и две идентичные циклоидальные направляющие. Перепад высот для каждой направляющей один и тот же и составляет 80--100 мм. Как видно из фотографии, циклоидальные направляющие могут иметь форму полуарки циклоиды. Планшет изготавливается из двух оргстеклянных пластин толщиной 2--4 мм, в одной из которых сделаны прорези, а другая является основанием. Демонстрацию проводят следующим образом. Планшет кладут на конденсор кодоскопа, установленного так, чтобы угол между плоскостью конденсора и горизонтальной плоскостью составлял 5--10^o. С помощью объектива планшет проецируют на вертикальный экран. Двумя пальцами устанавливают шарики в верхних точках выбранных направляющих. Одновременно отпускают шарики без начальной скорости сначала по прямой и циклоидальной направляющим, затем по циклоидальной и произвольной направляющим. При этом учащиеся убеждаются, что время движения по циклоиде действительно минимально. Фактически этот опыт качественно доказывает, что циклоида является брахистохроной. Чтобы продемонстрировать таутохронные свойства циклоиды, шарики запускают из различных точек циклоидальных траекторий. При проведении этих опытов аудитории кажется, что шарики движутся в вертикальной плоскости, но с очень небольшим "ускорением свободного падения".

1. Берман Г.Н. Циклоида. --- М.: Гостехтеориздат, 1954. --- С. 100--114.

2. Майер В.В., Майер Р.В. Экспериментальное изучение брахистохронных и таутохронных свойств циклоиды / Ред. журн."Изв. вузов. Физика". --- Томск, 1990. --- 33 с. --- Деп. в ВИНИТИ 28.11.90, N 6380--В90.

3. Майер В.В., Майер Р.В. Устройство для демонстрации брахисто-- и таутохронных свойств циклоиды: Патент N 2029990 С1, МКИ G09B 23/06.

Майер В.В., Майер Р.В. Удивительные свойства циклоиды // Учебная физика. --- 1998. --- N 2. --- С. 22--26.