Майер Р.В. Использование компьютерных моделей при изучении механики

МАЙЕР Р.В.

ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНЫХ МОДЕЛЕЙ ПРИ ИЗУЧЕНИИ МЕХАНИКИ

Приведены примеры решения некоторых задач механики на ПЭВМ. Используются традиционные методы и алгоритмы, рассматриваемые в литературе, посвященной основам вычислительной математики и физики. Предложенные задачи и программы могут быть использованы при изучении механики, а также основ компьютерного моделирования.

1. ОСНОВЫ КИНЕМАТИКИ

Задача 1.1. Первые t₁=8 с точка двигалась с ускорением a₁(t)=1*t. До момента t₂=30 с ускорение точки a₂=0,2 м/с, после чего движение происходит с ускорением a₃=-4 м/с. Постройте графики зависимостей координаты, скорости и ускорения от времени, если начальные координата и скорость точки равны -200 м и -15 м/с.

 ====== Программа ПР -- 1.1.
SCREEN 12: dt = .002: x = -200: v = -15           'QBASIC
WHILE INKEY$ = ""
IF t < 8 THEN a = 1 * t ELSE IF t < 30 THEN a = .2 ELSE a = -4
v = v + a * dt: x = x + v * dt: t = t + dt
CIRCLE (10*t+10, 240-.5*x), 2 : CIRCLE (10*t+10, 240-10*v), 1
CIRCLE (10 * t + 10, 240 - 10 * a), 1
WEND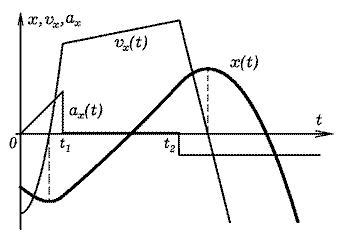

Задача 1.2. Точка движется по закону: x=3 cos(t) , y=2 cos(3.7t+2). Вычислите координаты x, y, проекции и модули скорости v_x, v_y, v и ускорения a_x, a_y, a, нормальное a_n и тангенциальное a_τ ускорения в последовательные моменты времени t=i Δt, i = 1, 2, 3, ...

 ===== Программа ПР -- 1.2. 
dt = .2: FOR t = 0 TO 10 STEP dt                  'QBASIC
x0 = x: y0 = y: vx0 = vx: vy0 = vy
x = 3 * COS(t): y = 2 * COS(3.7 * t + 2)
vx = (x - x0) / dt: vy = (y - y0) / dt
ax = (vx - vx0) / dt: ay = (vy - vy0) / dt
vv = SQR(vx * vx + vy * vy): aa = SQR(ax * ax + ay * ay)
cosa = (ax * vx + ay * vy) / (aa * vv): at = aa * cosa:
IF at < aa THEN an = SQR(aa * aa - (at * at))
PRINT t; x; y; vv; aa; at; an
NEXT

2. ДИНАМИКА СИСТЕМЫ ЧАСТИЦ

Задача 2.1. Камень бросили под углом α к горизонту со скоростью v₀. Сила сопротивления воздуха пропорциональна скорости: F=rv. Определите координаты и скорость камня в последующие моменты времени t. Постройте положения камня через равные промежутки времени.

 ===== Программа ПР -- 2.1. 
SCREEN 12                                         'QBASIC
m = 1: r = .5: g = 10: dt = .002: x = 0: y = 1: vx = 30: vy = 30
LINE (0, 400)-(640, 400): LINE (20, 0)-(20, 480)
WHILE y > 0
t = t + dt: k = k + 1
ax = -r * vx / m: ay = (-m * g - r * vy) / m
vx = vx + ax * dt: x = x + vx * dt
vy = vy + ay * dt: y = y + vy * dt
PSET (20 + 10 * x, 400 - 10 * y), 15
IF k / 50 = INT(k / 50) THEN CIRCLE (20 + 10 * x, 400 - 10 * y), 4
WEND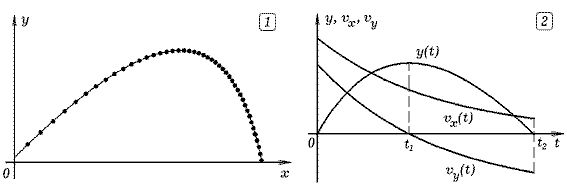

Задача 2.2. Тело брошено под углом к горизонту. Постройте графики зависимости координаты y тела и проекций его скорости от времени. Убедитесь в том, что время подъема меньше времени спуска. Сила сопротивления воздуха пропорциональна скорости.

 ===== Программа ПР -- 2.2. 
SCREEN 12                                         'QBASIC
m = 1: r = 2: g = 10: dt = .002: x = 0: y = .01
v = 10: A = 3.14 / 5
vx = v * COS(A): vy = v * SIN(A)
LINE (0, 300)-(640, 300): LINE (20, 0)-(20, 480)
WHILE y > 0
t = t + dt: ax = -r * vx / m: ay = (-m * g - r * vy) / m
vx = vx + ax * dt: x = x + vx * dt
vy = vy + ay * dt: y = y + vy * dt
CIRCLE (20 + 500 * t, 300 - 25 * vx), 1
CIRCLE (20 + 500 * t, 300 - 25 * vy), 1
CIRCLE (20 + 500 * t, 300 - 150 * y), 1
WEND

3. ДИНАМИКА ТВЕРДОГО ТЕЛА

Задача 3.1. Имеется неоднородная пластина, ограниченная функцией y=x^1/2, осью абсцисс, прямой x=2, плотность которой равна ρ(x,y)=2+0,4y+0,2x². Найдите момент инерции пластины относительно оси Ox.

 ===== Программа ПР -- 3.1. 
dx = .05: dy = .05: h = .02                       'QBASIC
FOR x = 0 TO 2 STEP dy
WHILE y < SQR(x)
y = y + dy: rho = 2 + .4 * y + .2 * x * x
dV = dx * dy * h: I = I + rho * dV * y * y
WEND: NEXT: PRINT I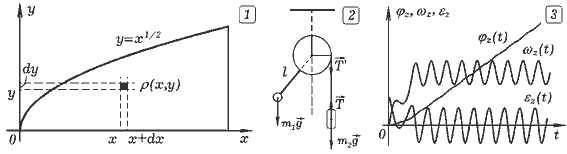

Задача 3.2. К шкиву массой m радиуса R, установленному на горизонтальной оси, с помощью невесомого стержня длиной l прикреплен груз массы m₁. На шкив намотана нить, к концу которой привязано тело массой m₂. При t=0 система покоилась. Рассчитайте угловые ускорение, скорость и перемещение шкива в последующие моменты времени, если тормозящий момент пропорционален скорости.

 ===== Программа ПР -- 3.2. 
SCREEN 12                                         'QBASIC
m1 = .1: m2 = .3: m = .1: R = .05: l = .1: dt = .001
FOR t = 0 TO 8 STEP dt
eps = (9.8 * m2 * R - 9.8 * m1 * l * SIN(fi) - .01 * w) / 
                          (m1 * l * l + (m2 + m / 2) * R * R)
fi = fi + w * dt: w = w + eps * dt
CIRCLE (10 + 100 * t, 400 - 10 * w), 1
CIRCLE (10 + 100 * t, 400 - 5 * fi), 1
CIRCLE (10 + 100 * t, 400 - 1 * eps), 1
NEXT

4. ЗАКОНЫ СОХРАНЕНИЯ

Задача 4.1. Рассчитайте движение ракеты, удаляющейся по прямой от Земли, если масса горючего уменьшается со скоростью b=const. Масса оболочки равна m_0, масса заправленной ракеты m>m₀. Относительная скорость вытекания газов равна v_отн. Постройте графики x(t), v_x(t), m(t).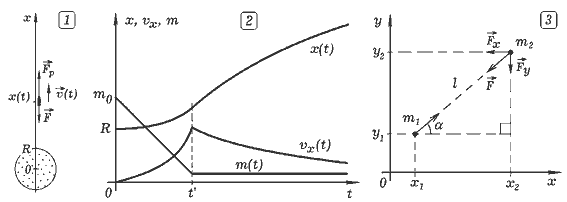

 ===== Программа ПР -- 4.1. 
SCREEN 12:  dt = .1: x = 50: m1 = 10              'QBASIC
b = 1: dt = .01: vot = 4: m0 = 1
LINE (0, 420)-(640, 420)
FOR t = 0 TO 100 STEP dt
m1 = m1 - b * dt: m2 = m1 - b * dt
IF m2 < m0 THEN b = 0
Fr = vot * (m1 - m2) / dt: F = 3000 / (x * x)
a = (Fr - F) / m1: v = v + a * dt: x = x + v * dt
CIRCLE (5 + 20 * t, 420 - 2.5 * x), 1
CIRCLE (5 + 20 * t, 420 - 18 * v), 1
CIRCLE (5 + 20 * t, 420 - 20 * m1), 1
NEXT

Задача 4.2. Промоделируйте движение двух МТ, взаимодействующих друг с другом: а) с силами отталкивания; б) с силами притяжения.

 ===== Программа ПР -- 4.2. 
SCREEN 12:  dt = .1: m1 = 1: m2 = 2               'QBASIC
x1 = 0: y1 = 200: v1x = 2: x2 = 640: y2 = 220: v2x = -2:
FOR t = 1 TO 1000 STEP dt: k = k + 1
ll = (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2)
cosA = (x2 - x1) / SQR(ll): sinA = (y2 - y1) / SQR(ll)
F = 500 / ll: a1x = -F * cosA / m1: a1y = -F * sinA / m1
v1x = v1x + a1x * dt: x1 = x1 + v1x * dt
v1y = v1y + a1y * dt: y1 = y1 + v1y * dt
a2x = F * cosA / m2: a2y = F * sinA / m2
v2x = v2x + a2x * dt: x2 = x2 + v2x * dt
v2y = v2y + a2y * dt: y2 = y2 + v2y * dt
PSET (x1, y1): PSET (x2, y2)
IF k / 100 = INT(k / 100) 
    THEN CIRCLE (x1, y1), 1: CIRCLE (x2, y2), 1
IF k / 100 = INT(k / 100) 
    THEN CIRCLE (x1, y1), 2: CIRCLE (x2, y2), 2
IF k / 100 = INT(k / 100) 
    THEN CIRCLE (x1, y1), 3: CIRCLE (x2, y2), 3
IF k / 100 = INT(k / 100) 
    THEN CIRCLE (x1, y1), 4: CIRCLE (x2, y2), 4
NEXT

5. СИЛЫ В МЕХАНИКЕ

Задача 5.1. Определите силу гравитационного притяжения, действующую со стороны шарообразного тела радиуса R на материальную точку массой m, находящуюся на расстоянии z' от центра. Плотность шара ρ(r)=100/r, где r --- расстояние от его центра.

 ===== Программа ПР -- 5.1. 
CLS: dr = .1: dtheta = .1: dfi = .2               'QBASIC
m = 1: rho1 = 100: z1 = 20
FOR r = 0 TO 3 STEP dr
FOR theta = 0 TO 3.14 STEP dtheta
FOR fi = 0 TO 6.28 STEP dfi
IF r < 1 THEN rho = 100 ELSE rho = 100 / r
z = r * COS(theta): y = r * SIN(theta) * SIN(fi)
x = r * SIN(theta) * COS(fi)
dm = rho * r * r * dtheta * dfi * dr
rast = SQR(x * x + y * y + (z1 - z) * (z1 - z))
l = z1 - r * COS(theta) 
F = F + m * dm * l / (rast * rast * rast)
NEXT: NEXT: PRINT F, r: NEXT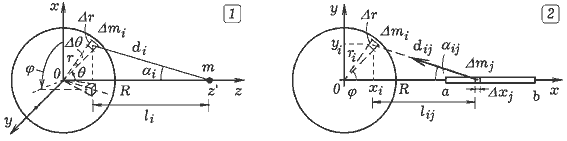

Задача 5.2. Определите силу гравитационного притяжения, действующую между неоднородным диском радиусом R, толщиной h и однородным стержнем массой m₁, концы которого имеют координаты a и b>R. Зависимость плотности диска от координаты: ρ(r)=100/r, где r --- расстояние от его центра O.

 ===== Программа ПР -- 5.2. 
CLS: dr = .1: dfi = .05: rho1 = 100               'QBASIC
dx1 = .1: dm1 = .2 * dx1: h = .1
FOR x1 = 5 TO 6 STEP dx1
FOR r = 0 TO 3 STEP dr
FOR fi = 0 TO 6.28 STEP dfi
IF r < 1 THEN rho = 100 ELSE rho = 100 / r
x = r * COS(fi): y = r * SIN(fi): dm = rho * h * r * dr * dfi
rast = SQR((x - x1) * (x - x1) + y * y): l = x1 - r * COS(fi)
F = F + dm1 * dm * l / (rast * rast * rast)
NEXT: NEXT: PRINT F, r, x1: NEXT

Задача 5.3. Три МТ массами m₁, m₂, m₃ имеют координаты (x₁, y₁, z₁), (x₂, y₂, z₂), (x₃, y₃, z₃). Рассчитайте напряженность поля во всех точках плоскости, содержащей эти МТ.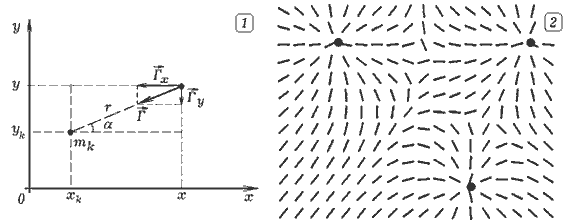

 ===== Программа ПР -- 5.3. 
uses crt, graph;                                  'PASCAL
var EC,D,DrV,MV,i,j,m1,m2,m3,x1,y1,x2,y2,x3,y3 : integer;
cosa1,cosa2,cosa3,sina1,sina2,sina3,
        a,a1,a2,r1,r2,r3,x,y,Gx,Gy,pi: real; Label metka;
BEGIN  
DrV:=Detect; InitGraph(DrV,MV,'c:\bp\bgi');
EC:=GraphResult; if EC<>grOK then Halt(1);
pi:=arctan(1)*4; x1:=150; y1:=240; m1:=15; 
x2:=300; y2:=100; m2:=20; x3:=450; y3:=400; m3:=10;
circle(x1,y1,2);circle(x2,y2,2);circle(x3,y3,2);
circle(x1,y1,4);circle(x2,y2,4);circle(x3,y3,4);
circle(x1,y1,6);circle(x2,y2,6);circle(x3,y3,6);
for i:=1 to 100 do for j:=1 to 100 do
begin x:=35*i; y:=35*j;
r1:=sqrt((x-x1)*(x-x1)+(y-y1)*(y-y1));
r2:=sqrt((x-x2)*(x-x2)+(y-y2)*(y-y2));
r3:=sqrt((x-x3)*(x-x3)+(y-y3)*(y-y3));
if (r1=0)or(r2=0)or(r3=0) then goto metka;
cosa1:=(x-x1)/r1; sina1:=(y-y1)/r1; 
cosa2:=(x-x2)/r2; sina2:=(y-y2)/r2;
cosa3:=(x-x3)/r3; sina3:=(y-y3)/r3;
Gx:=m1*cosa1/(r1*r1)+m2*cosa2/(r2*r2)+m3*cosa3/(r3*r3);
Gy:=m1*sina1/(r1*r1)+m2*sina2/(r2*r2)+m3*sina3/(r3*r3);
if Gx<>0 then a:=arctan(Gy/Gx) else a:=pi/2;
line(35*i-round(12*cos(a)),35*j-round(12*sin(a)),
                 35*i+round(12*cos(a)),35*j+round(12*sin(a)));
line(35*i-round(12*cos(a))+1,35*j-round(12*sin(a)),
               35*i+round(12*cos(a))+1,35*j+round(12*sin(a)));
line(35*i-round(12*cos(a)),35*j-round(12*sin(a))+1,
               35*i+round(12*cos(a)),35*j+round(12*sin(a))+1);
line(35*i-round(12*cos(a)),35*j-round(12*sin(a))-1,
               35*i+round(12*cos(a)),35*j+round(12*sin(a))-1);
metka: end; Repeat until Keypressed; CloseGraph;
END.

Задача 5.4. Рассчитайте силовые линии гравитационного поля, созданного несколькими материальными точками в безграничной среде. Используйте метод покоординатного спуска.

 ===== Программа ПР -- 5.4. 
uses crt, graph;
var EC,D,DrV,MV,i,j,m1,m2,m3,x1,y1,x2,y2,x3,y3,k : integer;
x0,y0,amax,max,fi1,fi,a,r1,r2,r3,x,y,pi: real;
Label metka;
Procedure Raschet;
begin
Repeat r1:=sqrt((x-x1)*(x-x1)+(y-y1)*(y-y1));
r2:=sqrt((x-x2)*(x-x2)+(y-y2)*(y-y2)); 
r3:=sqrt((x-x3)*(x-x3)+(y-y3)*(y-y3));
fi:=-(m1/r1)-(m2/r2)-(m3/r3); max:=0; x0:=x; y0:=y;
for i:=1 to 90 do begin a:=2*pi*i/90; x:=x0+cos(a); y:=y0+sin(a);
r1:=sqrt((x-x1)*(x-x1)+(y-y1)*(y-y1)); 
r2:=sqrt((x-x2)*(x-x2)+(y-y2)*(y-y2));
r3:=sqrt((x-x3)*(x-x3)+(y-y3)*(y-y3)); 
fi1:=-(m1/r1)-(m2/r2)-(m3/r3);
if fi1-fi>max then begin max:=fi1-fi; amax:=a; end;
end; k:=k+1; x:=x0+cos(amax); y:=y0+sin(amax);
circle(round(x),round(y),1);
until k>500;
end;
BEGIN  DrV:=Detect; InitGraph(DrV,MV,'c:\bp\bgi');
       EC:=GraphResult; if EC<>grOK then Halt(1);
pi:=arctan(1)*4; x1:=250; y1:=240; m1:=10;
x2:=300; y2:=100; m2:=20; x3:=400; y3:=300; m3:=10;
circle(x1,y1,2);circle(x2,y2,2);circle(x3,y3,2);
for j:=1 to 20 do begin
x:=250+1*cos(0.314*j); y:=240+1*sin(0.314*j); Raschet; k:=0;
end; Repeat until Keypressed; CloseGraph;
END.

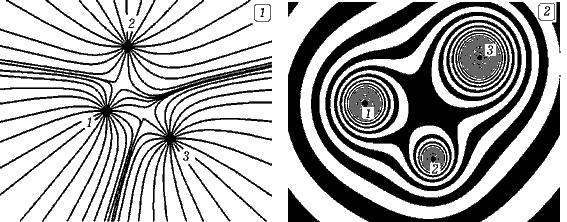
Задача 5.5. Рассчитайте распределение потенциала гравитационного поля нескольких МТ на плоскости, содержащей эти МТ.

 ===== Программа ПР -- 5.5. 
uses crt, graph;                                  'PASCAL
var r1,r2,r3,x1,x2,x3,y1,y2,y3,fi,m1,m2,m3 :real; 
Gd,Gm,i,j :integer;
BEGIN
Gd:= Detect; InitGraph(Gd, Gm, 'c:\bp\bgi\');
if GraphResult <> grOk then Halt(1);
m1:=15; m2:=23; m3:=8; { m1:=8; m2:=46;}
x1:=180.5; y1:=180.5; x2:=400.5; 
y2:=220.5; x3:=240.5; y3:=340.5;
For i:=0 to 640 do For j:=0 to 480 do
begin 
r1:=sqrt(sqr(x1-i)+sqr(y1-j)); r2:=sqrt(sqr(x2-i)+sqr(y2-j));
r3:=sqrt(sqr(x3-i)+sqr(y3-j)); fi:=m1/r1+m2/r2+m3/r3;
{putpixel(i,j,round((fi+1)*20));} 
if round(fi/0.05)-fi/0.05<0.002 then putpixel(i,j,15);
end; 
Repeat until Keypressed; CloseGraph;
END.

7. АНАЛИТИЧЕСКАЯ ДИНАМИКА

Задача 7.1. Промоделируйте расползание пятна в фазовом пространстве в случае свободных незатухающих, затухающих, а также вынужденных колебаний математического маятника.

 ===== Программа ПР -- 7.1. 
uses crt, graph;                                  'PASCAL
Const m= 1; k = 4; r = 0.5; dt = 0.002; pi = 3.1415926; 
var i,j,Gd,Gm: integer; 
x,y,z,v,a,f,zz,zzz,t,dx,dy,dz,vx,vy,vz: real;
BEGIN Gd := Detect;  InitGraph(Gd, Gm, 'c:\bp\bgi');
      if GraphResult <> grOk then Halt(1);
line(180,0,180,480);  line(0,280,640,280);
For i:=1 to 40 do For j:=1 to 40 do begin
x:=1+0.04*i; v:=0.04*j; t:=0;
Repeat t:= t + dt; 
a:=(f-k*sin(x)-r*v)/m; v:=v+a*dt; x:=x+v*dt;
until t>5;
putpixel(round(50*x)+180,280-round(50*v),15);
circle(round(50*x)+180,280-round(50*v),1);
end; Repeat until KeyPressed; CloseGraph;
END.

Программа рассчитывает состояние ансамбля осцилляторов и позволяет изучить изменение формы фазового объема в случае свободных незатухающих, затухающих и вынужденных колебаний математического маятника.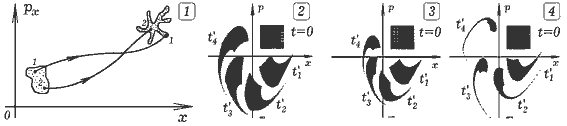

Расползание фазового пятна в случае незатухающих колебаний математического маятника: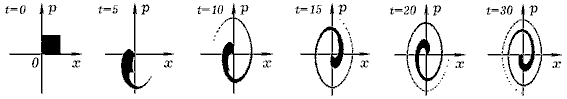

Сжатие фазового пятна в случае затухающих колебаний: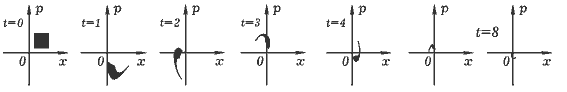

Задача 7.2. Камень брошен вертикально вверх со скоростью v=10 м/c так, что в момент t₁=0 его координата y₁=0, а в момент t₂=1 c она равна y₂=5 м. Численным методом найдите действие S для действительного пути. Варьируя коэффициенты в уравнении движения y=C₁t²/2+C₂t+C₃, определите действие S' при движении по окольным путям, и убедитесь в том, что оно всегда больше.

 ===== Программа ПР -- 7.2. 
uses crt, graph;                                  'PASCAL
const m=1; dt=0.00005; g=10;
var y,vy,s,ds,ds1,t,C1,c2,c3,c4:real; Gd,Gm,i : integer;
BEGIN  
Gd:= Detect; InitGraph(Gd, Gm, 'c:\bp\bgi');
if GraphResult <> grOk then Halt(1);
line(0,0,640,0); line(0,0,0,480);
For i:=1 to 70 do
begin S:=0; t:=0; C1:=-13+i*0.2; C2:=5-C1/2;
Repeat y:=C2*t+C1*t*t/2; vy:=C2+C1*t;
dS:=m*(vy*vy/2-g*y)*dt; s:=s+ds; t:=t+dt;
until t>1; circle(round(C1*40)+500,round(-S*20),1);
end; Repeat until keypressed;
END.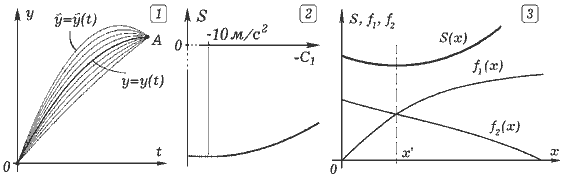

Задача 7.3. Электрон движется из точки A области с потенциалом φ₁ в точку B другой области с потенциалом φ₂. При переходе плоской границы раздела областей происходит "преломление" траектории в точке C. Задавшись скоростью v₁ в первой области, рассчитать действие S при различных положениях точки C, если время движения из A в B фиксировано.

 ===== Программа ПР -- 7.3. 
uses crt, graph;                                  'PASCAL
var h2,h1,pi,t,alpha,sinusA,sinusB,x,v1,v2,
                 k,z,q,s,ds,t1,t2,dx: real;
    i: integer; Gd, Gm : integer; x1,x2,y1,y2: integer;
const m=0.1; h=0.1; g=10; a=2;
BEGIN 
Gd:= Detect;  InitGraph(Gd, Gm, 'c:\bp\bgi\');
if GraphResult <> grOk then Halt(1);
pi:=3.1415; h1:=1; v1:=1; alpha:=0.5;
v2:=sqrt(v1*v1+2*g*h); sinusB:=v1*sin(alpha)/v2;
x:=h1*sin(alpha)/cos(alpha);
h2:=(a-x)*sqrt(1-sinusB*sinusB)/sinusB;
t1:=sqrt(h1*h1+sqr(x))/v1; t2:=sqrt(h2*h2+sqr(a-x))/v2;
t:=t1+t2; line(round(x*230+35),150,round(x*230+35),380);
line(10,450,600,450); line(35,50,35,470); x:=0; dx:= 0.01;
For i:=0 to 200 do
begin x:=x+dx; t1:=sqrt(h1*h1+x*x)/v1; t2:=t-t1;
v2:=sqrt(h2*h2+(a-x)*(a-x))/t2;
s:=(m*v1*v1/2-m*g*h)*t1+m*v2*v2/2*t2;
circle(round(x*230+35),round(-S*1500+800),2);
sinusA:=x/sqrt(h1*h1+x*x);
sinusB:=(a-x)/sqrt(h2*h2+(a-x)*(a-x));
circle(round(x*230+35),round(-250*sinusA*v1+450),1);
circle(round(x*230+35),round(-250*sinusB*v2+450),1);
end; Repeat until keypressed; CloseGraph;
END.

8. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ

Задача 8.1. Колебательная система состоит из тела массой m, находящегося на пружине с жесткостью k в вязкой среде с коэффициентом сопротивления r. Систему вывели из состояния равновесия и предоставили самой себе. Изучите возникающие колебания.

 ===== Программа ПР -- 8.1. 
SCREEN 12                                         'QBASIC
m = .1: k = 10: r = .1: w = 9.5: dt = .001: x = 15      
WHILE INKEY$ = ""
t = t + dt : F = 0: REM F = 10 * SIN(w * t)
a = (F - k * x - r * v) / m : v = v + a * dt 
x = x + v * dt
CIRCLE (100 * t + 10, 240 - 5 * x), 1 
CIRCLE (100 * t + 10, 240 - 1 * v), 2
CIRCLE (100 * t + 10, 100 - 1 * F), 1 
'CIRCLE (320 + 10 * x, 240 - 1 * v), 1
WEND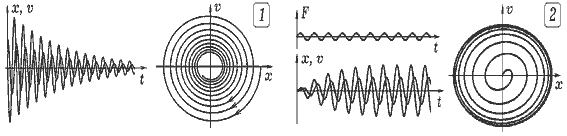

Задача 8.2. На пружинный маятник, состоящий из тела на пружине, действует внешняя гармоническая сила. Получите графики зависимостей x(t), v_x(t), a_x(t), постройте фазовый портрет системы.

Задача 8.3. Исследуйте автоколебательную систему, которая посредством положительной обратной связи сама регулирует поступление энергии от источника. Пусть вблизи положения равновесия, когда -b < x < b и тело движется в направлении оси OX, на него действует постоянная сила F_m. Постройте графики x(t), v_x(t), a_x(t), и фазовый портрет системы.

 ===== Программа ПР -- 8.3. 
SCREEN 12                                        'QBASIC
m = 1: k = 1: r = .03: dt = .001: x = 0: v = .01  
LINE (0, 240)-(640, 240): LINE (0, 241)-(640, 241)
WHILE INKEY$ = ""
IF (.3 - ABS(x) > 0) AND (v > 0) THEN F = 3 ELSE F = 0
t = t + dt : a = (F - k * x - r * v) / m 
v = v + a * dt : x = x + v * dt
CIRCLE (15 * t + 10, 240 - 15 * x), 2 
CIRCLE (15 * t + 10, 240 - 40 * v), 1
'CIRCLE (320 + 50 * x, 240 - 40 * v), 1
WEND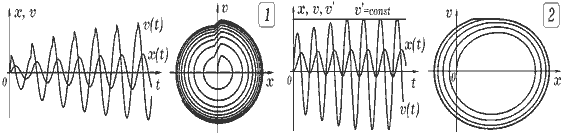

Задача 8.4. Промоделируйте фрикционный маятник Фроуда, состоящий из физического маятника, висящего на вращающемся валу. Сила трения между валом и маятником убывает по экспоненциальному закону F_тр=F₀e^{-β |v - x'_t|}. Постройте график φ(t), ω(t) и фазовую кривую.

 ===== Программа ПР -- 8.4. 
SCREEN 12                                         'QBASIC
m = 1: k = 1: r = .05: dt = .005: vv = 2: x = 0: v = .01
LINE (10, 0)-(10, 480): LINE (0, 240)-(640, 240)
WHILE INKEY$ = ""
IF ((vv - v) > 0) THEN z = 1 ELSE z = -1
F = 1.6 * z * EXP(-.1 * ABS(v - vv))
t = t + dt: a = (F - k * x - r * v) / m
v = v + a * dt: x = x + v * dt
CIRCLE (10 * t + 10, 240 - 20 * x), 2
CIRCLE (10 * t + 10, 240 - 100 * v), 1
CIRCLE (10 * t + 10, 240 - 100 * vv), 1
CIRCLE (180 + 100 * x, 240 - 100 * v), 2
WEND: END

9. ВОЛНОВОЕ ДВИЖЕНИЕ

Задача 9.1. Промоделируйте распространение одиночного импульса в одномерной упругой среде, его отражение и прохождение границы раздела двух сред.

 ===== Программа ПР -- 9.1. 
uses crt, graph; const n=200; h=1; dt=0.05;       'PASCAL
var  i, j, DriverVar,ModeVar, ErrorCode : integer;
eta,xi,xxii : array[1..N] of real; t, vv : real;
Procedure Graph_Init;
begin {- Инициализация графики -}
DriverVar:=Detect;   
InitGraph(DriverVar,ModeVar,'c:\bp\bgi');
ErrorCode:=GraphResult; if ErrorCode<>grOK then Halt(1);
end;
Procedure Raschet; {Расчет смещения}
  begin for i:=2 to N-1 do begin xxii[i]:=xi[i];
  if i<N/2 then vv:=4 else vv:=0.5;
  eta[i]:=eta[i]+vv*(xi[i+1]-2*xi[i]+xi[i-1])/(h*h)*dt;  
  end;
  for i:=2 to N-1 do xi[i]:=xi[i]+eta[i]*dt;
  xi[N]:=0;      { Конец закреплен}
{ xi[N]:=xi[N-1];}{ незакрепленный}  end;
Procedure Draw; 
  begin        {- Вывод на экран -}
  setcolor(black); line(i*3-3,240-round(xxii[i-1]*50),
                           i*3,240-round(xxii[i]*50));
    setcolor(white); line(i*3-3,240-round(xi[i-1]*50),
                       i*3,240-round(xi[i]*50));  end;
BEGIN      {- Основная программа -}
  Graph_Init;  Repeat t:=t+dt;
    if t<6.28 then xi[1]:=2*sin(t) else xi[1]:=0;
    Raschet; For i:=1 to N do Draw;
  until KeyPressed; CloseGraph;
END.

Задача 9.2. Имеется прямоугольная пластина, некоторые элементы которой совершает колебания, а другие --- не способны колебаться. Края пластины закреплены. Изучите распространение, отражение, интерференцию и дифракцию упругой волны в двумерной среде.

Задача 9.3. Рассчитайте интерференционную картину от двух источников, удаленных друг от друга на расстоянии 2d, в плоскости, содержащей источники. Интенсивности волн равны I, длина волны λ.

 ===== Программа ПР -- 9.2. 
SCREEN 12: pi = 3.1415: Lambda = 60: d = 60       'QBASIC
x1 = 320 - d: x2 = 320 + d: y1 = 340
FOR x = 1 TO 640 STEP 2
FOR y = 1 TO 480 STEP 2
l1 = SQR((x - x1) * (x - x1) + (y - y1) * (y - y1))
l2 = SQR((x - x2) * (x - x2) + (y - y1) * (y - y1))
I1 = 5000 / (l1 * l1): I2 = 5000 / (l2 * l2)
I = I1 + I2 + 2 * SQR(I1 * I2) * COS(2 * pi * (l1 - l2) / Lambda)
IF I > .2 THEN PSET (x, y)
IF I > 2 THEN CIRCLE (x, y), 1
NEXT
NEXT

10. МЕХАНИКА ЖИДКОСТИ И ГАЗА

Задача 10.1. Рассчитайте установившееся потенциальное течение идеальной жидкости по трубе прямоугольного сечения. Внутри трубы имеются выступы и различные препятствия. Постройте линии тока.

 ===== Программа ПР -- 10.1. 
uses crt, graph; const n=140; m=50;               'PASCAL
var i,ii,j,jj,k,DriverVar, ModeVar, ErrorCode : integer;
psi: array[1..N, 1..M] of real;
procedure Raschet; {---- Расчет потенциала ----}
begin 
psi[i,j]:=(psi[i+1,j]+psi[i-1,j]+psi[i,j+1]+psi[i,j-1])/4;
end;
procedure Gran_usl; {---- Граничные условия ----}
begin for i:=1 to N do
begin psi[i,2]:=-200; psi[i,M-1]:=200; 
      psi[i,1]:=-200; psi[i,M]:=200;
end;
for j:=1 to M do begin psi[N-1,j]:=-204+8*j; 
                         psi[N,j]:=-204+8*j; end;
for j:=1 to 25 do begin
psi[2,j]:=-204+16*j; psi[N-1,j]:=-204+8*j;
psi[1,j]:=-204+16*j; psi[N,j]:=-204+8*j; end;
for i:=1 to N do for j:=1 to M do
if (j>25)and((i-60)*(i-60)+(j-25)*(j-25)<200) 
                                then psi[i,j]:=0;
for i:=1 to N do for j:=1 to M do
if (abs(j-25)<15)and(abs(i-110)<5) then psi[i,j]:=0;
for i:=1 to N do for j:=1 to M do
if (j>25)and(i<30) then psi[i,j]:=200;
end;
procedure Draw; {---- Вывод на экран ----}
begin
if psi[i,j]>-200 then setcolor(14);
if psi[i,j]>-150 then setcolor(0);
if psi[i,j]>-100 then setcolor(2);  
if psi[i,j]>-50 then setcolor(4);
if psi[i,j]>0  then setcolor(6);    
if psi[i,j]>50  then setcolor(8);
if psi[i,j]>100  then setcolor(10); 
if psi[i,j]>150 then setcolor(12);
{setcolor(round((psi[i,j]+200)/35));}
{if round(psi[i,j]/75)25)and((i-60)*(i-60)+(j-25)*(j-25)<200) 
                then setcolor(0);
if (j>25)and(i<30) then setcolor(0);
if (abs(j-25)<15)and(abs(i-110)<5) then setcolor(0);
rectangle(i*4+50,j*4,i*4+53,j*4+3);
rectangle(i*4+51,j*4+1,i*4+52,j*4+2);
end;
BEGIN             {---- Основная программа ----}
begin DriverVar:=Detect; 
InitGraph(DriverVar,ModeVar,'c:\bp\bgi');
ErrorCode:=GraphResult; 
if ErrorCode <> grOK then Halt(1); end;
Repeat inc(k);
Gran_usl; For i:=2 to N-1 do For j:=2 to M-1 do Raschet;
Gran_usl; For j:=2 to M-1 do For i:=2 to N-1 do Raschet;
Gran_usl; For i:=2 to N-1 do For jj:=2 to M-1 do
                          begin j:=M+1-jj; Raschet; end;
Gran_usl; For j:=2 to M-1 do For ii:=2 to N-1 do
                          begin i:=N+1-ii; Raschet; end;
if k/50=round(k/50) then begin cleardevice;
For i:=2 to N-1 do For j:=2 to M-1 do Draw; end;
until KeyPressed; CloseGraph;
END.

Задача 10.2. Исследуйте установившееся безвихревое течение вязкой жидкости в бесконечно длинной трубе (канале) постоянного сечения, внутри которой движется бесконечно длинное тело.

 ===== Программа ПР -- 10.2. 
uses crt, graph;                                  'PASCAL
const n= 90; m=58; h=1; dt=0.02;                  
var  i,j,ii,jj,kk,DV,MV,EC : integer;
vv, v: array[1..N, 1..M] of real; 
procedure Gr_usl; {---- Граничные условия ----}
begin
for i:=1 to N do for j:=1 to M do v[i,j]:=vv[i,j];
for i:=2 to N-1 do for j:=2 to M-1 do begin
if (j<5)and(abs(5-i)<5) then v[i,j]:=0;
if (j<40)and(abs(i-50)<1+20*sqr(cos(j/25))) then v[i,j]:=300;
end; for i:=1 to N do v[i,M]:=0;
for j:=1 to M do begin v[1,j]:=0; v[N,j]:=0; end;
end;                                    
procedure Raschet; {---- Расчет скорости ----}
begin vv[i,j]:=v[i,j]+(v[i,j+1]-2*v[i,j]+v[i,j-1])*dt/(h*h)
+(v[i+1,j]-2*v[i,j]+v[i-1,j])*dt/(h*h); end;
procedure Draw;{---- Вывод на экран ----}
begin
setcolor(round(v[i,j]/40));
if v[i,j]<1 then setcolor(9);
{if round(v[i,j]/60) grOK then Halt(1);
Repeat Gr_usl; 
       For i:=1 to N-1 do For j:=2 to M-1 do Raschet;
       Gr_usl; For jj:=2 to M-1 do For ii:=1 to N-1 do
               begin i:=N+1-ii; j:=M+1-jj; Raschet; end;
       For i:=1 to N do vv[i,1]:=vv[i,2];
       kk:=kk+1; if kk/30=round(kk/30) then
       For i:=2 to N-1 do For j:=2 to M-1 do Draw;
until KeyPressed; CloseGraph;
END.

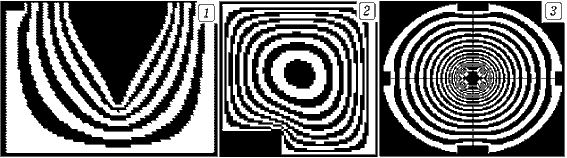
Задача 10.3. Рассчитайте течение вязкой жидкости в бесконечно длинной трубе произвольного сечения при наличии разности давлений на концах трубы.

11. ОСНОВЫ НЕРЕГУЛЯРНОЙ ДИНАМИКИ

Задача 11.1. Изучите движение шарика в биллиарде Синная прямоугольной формы, имеющем наклонные стенки и конус в центре.

 ===== Программа ПР -- 11.1. 
uses dos, crt, graph;                             'PASCAL
const dt=0.03;
var m,Fx,Fy,x,y,vx,vy,xx,yy,x1,y1 : real;
    Gd,Gm,i,j :integer; ax,ay,F,l : real;
BEGIN
Gd:=Detect; InitGraph(Gd, Gm, 'c:\bp\bgi');
if GraphResult <> grOk then Halt(1);
m:=0.001; x1:=150; y1:=150; x:=100; 
y:=100; vx:=30; vy:=10;
Repeat
 Fx:=0; Fy:=0; l:=sqrt(sqr(x1-x)+sqr(y1-y)); 
 if l<10 then F:=-0.03;
 if x<80 then Fx:=0.05; if x>220 then Fx:=-0.05;
 if y<80 then Fy:=0.05; if y>220 then Fy:=-0.05;
 Fx:=Fx+F*(x1-x)/l; Fy:=Fy+F*(y1-y)/l; ax:=Fx/m; ay:=Fy/m;
 xx:=x; yy:=y; vx:=vx+ax*dt; vy:=vy+ay*dt;  
 x:=x+vx*dt; y:=y+vy*dt; 
 delay(50); circle(50+round(x),240-round(vx),1);
{setcolor(8);  circle(round(xx),round(yy),2);}
 setcolor(15); circle(round(x),round(y),2);
until KeyPressed; 
Repeat until keypressed; CloseGraph;
END.

Задача 11.2. Логистическое отображение задается рекурсивной процедурой: x_i+1=ax_i(1-x_i). Изменяя бифуркационный параметр a, исследуйте процесс перехода в хаотический режим. Как ведет себя показатель устойчивости Ляпунова?

 ===== Программа ПР -- 11.2. 
uses crt, graph;                                  'PASCAL
const N=500; dt=0.001;
var ErrorCode,Detect,DriverVar,ModeVar, i, j : integer;
l,a,x,e,y,z,delta: real;
BEGIN
  DriverVar:=Detect; InitGraph(DriverVar,ModeVar,'c:\bp\bgi');
  ErrorCode:=GraphResult; if ErrorCode<>grOK then Halt(1);
  line(0,460,640,460); line(0,50,640,50); a:=2; e:=0.0001;
Repeat x:=0.05; y:=x+e; z:=x-e; a:=a+0.001; delta:=0;
for i:=1 to 600 do if abs(a*x*(1-x))<10 then begin
x:=a*x*(1-x); y:=a*y*(1-y); z:=a*z*(1-z);
if i>300 then delta:=delta+abs(y-x+z-x);
if i>100 then putpixel(round(300*a)-600,460-round(300*x),15); 
end;
l:=ln(0.0000000000000000000001+(delta/2/e/300));
circle(round(300*a)-600,50-round(2*l),1);
until (a>4) or (Keypressed);
Repeat until Keypressed; CloseGraph;
END.

Задача 11.3. Промоделируйте колебания маятника в потенциальной яме, у которой на месте одного постепенно появляется два углубления, разделенные плавно увеличивающимся потенциальным барьером. Изучите бифуркацию типа "вил".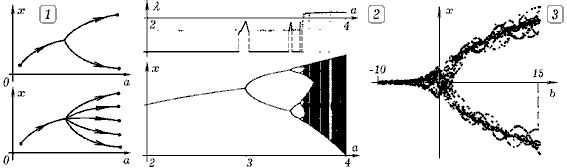

 ===== Программа ПР -- 11.3. 
uses crt, graph;                                  'PASCAL
const pi = 3.1415926; dt = 0.001; m= 1; 
      k = 4; r = 0.9; w = 2.3;
var i,j,Gd,Gm: integer; b,f,fi,t,z,zz,x,v,a: real;
BEGIN Randomize;
Gd := Detect; InitGraph(Gd, Gm, 'c:\bp\bgi');
if GraphResult <> grOk then Halt(1);
for j:=0 to 1000 do begin
b:=-10+0.025*j; x:= 0; v:= 0; t:=0; fi:=random(10);
for i:=0 to 10000 do begin t:= t + dt; f:=2*sin(w*t+fi);
a:=(f-k*(x*x*x-b*x)-r*v)/m; v:=v+a*dt; x:=x+v*dt; z:=SIN(w*t);
IF (z>0)and(zz<0)and(t>1) THEN 
                 circle(round(20*b)+200, 240-round(50*x),1);
IF (z>0)and(zz<0)and(t>1) THEN 
                 circle(round(20*b)+200, 240-round(50*x),2);
zz:= z;
end; end; Repeat until KeyPressed; CloseGraph;
END.

Задача 11.4. Промоделируйте перемешивание фазового объема в случае свободных незатухающих колебаний маятника Дафинга.

 ===== Программа ПР -- 11.4. 
uses crt, graph;                                  'PASCAL
Const m= 1; k = 4; dt = 0.002; pi = 3.1415926;
var i,j, Gd, Gm: integer; 
v,a,f,zz,zzz,t, x,y,z,dx,dy,dz,vx,vy,vz: real;
BEGIN Gd := Detect;  InitGraph(Gd, Gm, 'c:\bp\bgi');
if GraphResult <> grOk then Halt(1);
line(200,0,200,480); line(0,280,640,280);
For i:=1 to 40 do For j:=1 to 40 do begin
x:=0.04*i; v:=0.04*j; t:=0;
Repeat t:=t+dt; a:=-(x*x*x-x)/m; v:=v+a*dt; x:=x+v*dt;
until t>2; circle(round(50*x)+200,280-round(50*v),1);
end; Repeat until KeyPressed; CloseGraph;
END.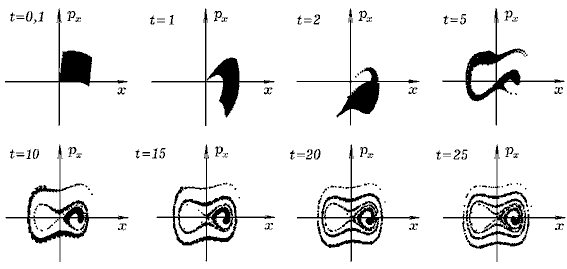

Задача 11.5. Получите сечения Пуанкаре для маятника Дафинга.

 ===== Программа ПР -- 11.5. 
uses crt, graph;                                  'PASCAL
const m = 1; k = 4; r = 0.5; w = 2.3;
      dt = 0.002; pi = 3.1415926;
var  Gd, Gm: integer; f,t,x,v,a,z,zz: real;
BEGIN x:= 0; v:= 0;
  Gd := Detect; InitGraph(Gd, Gm, 'c:\bp\bgi');
  if GraphResult <> grOk then Halt(1);
  line(200,0,200,480); line(0,280,640,280);
Repeat t:= t + dt; f:=1*sin(w*t);
a:=(f-k*(x*x*x-x)-r*v)/m; v:=v+a*dt; 
x:=x+v*dt; z:=SIN(w*t+3*pi/4);
IF (z>0)and(zz < 0) 
  THEN circle(round(100*x) + 200, 280 - round(100*v),1);
zz:= z; until (t>10000);
Repeat until KeyPressed; CloseGraph;
END.

Задача 11.6. Исследуйте странный аттрактор Реслера, задаваемый системой уравнений:

x' = - (y + z), y' = x + y/5, z' = 1/5 + z( x - μ).

 ===== Программа ПР -- 11.6. 
uses crt, Graph;                                 'PASCAL
Const a=15; b=30; c=2.2; dt=0.001; m=4.9;
var Gd,Gm: integer; t,x,y,z,dx,dy,dz,vx,vy,vz: real;
BEGIN Gd := Detect; InitGraph(Gd, Gm, 'c:\bp\bgi');
if GraphResult <> grOk then Halt(1); x:=2; y:=2; z:=1;
line(300,0,300,480); line(0,220,640,220);
Repeat t:=t+dt; dx:=-(y+z)*dt; x:=x+dx; vx:=dx/dt;
dy:=(x+y/5)*dt; y:=y+dy; vy:=dy/dt;
dz:=(0.2+z*(x-m))*dt; z:=z+dz; vz:=dz/dt;
if t>20 then putpixel(300+round(14*x),220-round(13*y),15);
until KeyPressed;
CloseGraph;
END.

Задача 11.7. Промоделируйте странный аттрактор Лоренца, уравнения которого имеют вид:

x' = a ( - x + y), y' = bx - y - xz, z' = - cz + xy.

 ===== Программа ПР -- 11.7. 
uses crt, graph;                                  'PASCAL
const a=15; b=30; c=2.2; dt=0.0001;                    
var  Gd, Gm: integer;
zz,zzz,t, x,y,z,dx,dy,dz,vx,vy,vz: real;
BEGIN  Gd:=Detect; InitGraph(Gd,Gm,'c:\bp\bgi');
       if GraphResult <> grOk then Halt(1);
  x:=20; y:=20; z:=5;
  Repeat t:=t+dt; dx:=a*(-x+y)*dt; x:=x+dx; vx:=dx/dt;
  dy:=(b*x-y-x*z)*dt; y:=y+dy; vy:=dy/dt;
  dz:=(-c*z+x*y)*dt; z:=z+dz;  vz:=dz/dt;
  putpixel(220+round(10*x),220-round(1*vx),15);
{ putpixel(220+round(10*y),220-round(1*vy),15);}
{ putpixel(100+round(10*z),220-round(1*vz),15);}
until KeyPressed; CloseGraph;
END.

12. НЕКОТОРЫЕ ЗАДАЧИ МЕХАНИКИ

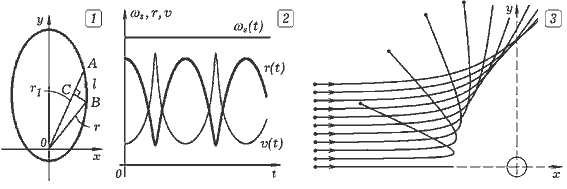
Задача 12.1. Рассчитайте траекторию тела в гравитационном поле Земли при различных начальных скоростях движения.

 ===== Программа ПР -- 12.1. 
SCREEN 12                                         'QBASIC
m1 = 10: m2 = 1000: dt = .0005:
LINE (0, 240)-(640, 240): LINE (320, 0)-(320, 480)
CIRCLE (320, 240), 100: CIRCLE (320, 240), 102
FOR i = 0 TO 5
x = 0: y = 20: vy = 0: vx = 2 * i + 1
FOR t = 0 TO 10 STEP dt
r = SQR(x * x + y * y): F = m1 * m2 / (r * r)
Fx = -F * x / r: Fy = -F * y / r: ax = Fx / m1: ay = Fy / m1
vx = vx + ax * dt: x = x + vx * dt
vy = vy + ay * dt: y = y + vy * dt
CIRCLE (320 + 10 * x, 240 - 10 * y), 1
NEXT: NEXT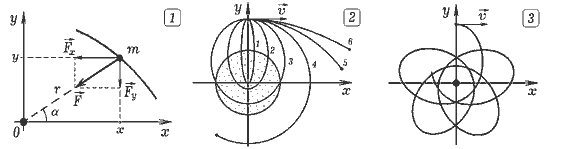

Задача 12.2. Промоделируйте движение тела в центрально симметричном поле, напряженность которого обратно пропорциональна r^2/3. Убедитесь в том, что траекторией является незамкнутая кривая.

 ===== Программа ПР -- 12.2. 
SCREEN 12                                         'QBASIC
m1 = 10: m2 = 1000: dt = .0002 
x = 0: y = 10: vx = 10: vy = 0 
LINE (0, 240)-(640, 240): LINE (320, 0)-(320, 480)
WHILE t < 50: t = t + dt
r = SQR(x * x + y * y): F = m1 * m2 / SQR(r * r * r)
Fx = -F * x / r: Fy = -F * y / r: ax = Fx / m1: ay = Fy / m1
vx = vx + ax * dt: x = x + vx * dt
vy = vy + ay * dt: y = y + vy * dt
CIRCLE (320 + 15 * x, 240 - 15 * y), 1
WEND

Задача 12.3. Планета вращается вокруг Солнца по эллиптической орбите. Постройте графики зависимости расстояния, линейной скорости и секториальной скорости планеты от времени. Подтвердите второй закон Кеплера, согласно которому секториальная скорость планеты остается постоянной.

 ===== Программа ПР -- 12.3. 
SCREEN 12: m1 = 10: m2 = 1000: dt = .002          'QBASIC
LINE (0, 400)-(640, 400): LINE (20, 0)-(20, 480)
x = 0: y = 20: vy = 0: vx = 4: r1 = SQR(x * x + y * y)
FOR t = 0 TO 30 STEP dt
r = SQR(x * x + y * y): F = m1 * m2 / (r * r)
Fx = -F * x / r: Fy = -F * y / r
ax = Fx / m1: ay = Fy / m1
vx = vx + ax * dt: x = x + vx * dt
vy = vy + ay * dt: y = y + vy * dt
dl = SQR((x - x1) * (x - x1) + (y - y1) * 
                      (y - y1) - (r - r1) * (r - r1))
dS = dl * r / 2: w = dS / (10 * dt)
x1 = x: y1 = y: r1 = r: v = SQR(vx * vx + vy * vy)
CIRCLE (20 + 20 * t, 400 - 60 * w), 1
CIRCLE (20 + 20 * t, 400 - 10 * r), 2
CIRCLE (20 + 20 * t, 400 - 10 * v), 1
NEXT

Задача 12.4. По направлению к массивному положительно заряженному ядру движутся альфа--частицы (опыт Резерфорда). Постройте траектории движения частиц при различных значениях прицельного параметра ρ.

 ===== Программа ПР -- 12.4. 
SCREEN 12: m1 = 1: m2 = 200: dt = .001            'QBASIC
LINE (0, 400)-(640, 400): LINE (320, 0)-(320, 480)
FOR i = 0 TO 30 STEP 3
x = -80: y = i: vx = 5: vy = 0
FOR t = 0 TO 30 STEP dt
r = SQR(x * x + y * y): F = -m1 * m2 / (r * r)
Fx = -F * x / r: Fy = -F * y / r: ax = Fx / m1: ay = Fy / m1
vx = vx + ax * dt: x = x + vx * dt
vy = vy + ay * dt: y = y + vy * dt
CIRCLE (320 + 5 * x, 400 - 5 * y), 1
NEXT: NEXT

Задача 12.5. Изучите затухающие колебания двух одинаковых маятников, каждый из которых состоит из тела массой m и пружины жесткостью k, связанных между собой упругой связью жесткостью q.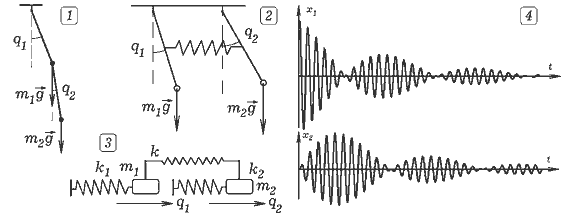

 ===== Программа ПР -- 12.5. 
SCREEN 12                                         'QBASIC
dt = .001: r = .2: k = 100: q = 8
t = 0: v = 15: x1 = .4: m = 1
DO
F = -q * (x1 - x2): a1 = (-F - r * v1 - k * x1) / m
x1 = x1 + v1 * dt
v1 = v1 + a1 * dt: a2 = (F - r * v2 - k * x2) / m
x2 = x2 + v2 * dt: 
v2 = v2 + a2 * dt: t = t + dt
CIRCLE (10 + 20 * t, 150 - 100 * x1), 1
CIRCLE (10 + 20 * t, 350 - 100 * x2), 1
LOOP UNTIL t > 40
END

13. ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ

Задача 13.1. В точке с координатами (x₁, 0, 0) в момент времени t (инерциальная система отсчета ИСО K₁) произошло событие A. Определите пространственную и временную координаты события A в ИСО K₂, движущейся со скоростью v=0,6c в направлении оси Ox. Вычислите и сравните пространственно--временные интервалы между событиями O и A в ИСО K и K'.

 ===== Программа ПР -- 13.1. 
CLS                                               'QBASIC
x1 = 2: x0 = 1: beta = .6: gamma = 1 / SQR(1 - beta * beta)
x11 = (x1 + beta * x0) * gamma: x01 = (x0 + beta * x1) * gamma
ss = SQR(x1 * x1 - x0 * x0): ss1 = SQR(x11 * x11 - x01 * x01)
PRINT x1, x0, x11, x01: PRINT "Интервал", ss, ss1
END

Майер Р.В. Математические начала современной теории механического движения: Учебное пособие. --- Глазов: ГГПИ, 2007. --- 164 с.

ВВЕРХ