"Физика как наука о наиболее общих законах природы, выступая в качестве учебного предмета в школе, вносит существенный вклад в систему знаний об окружающем мире. Она раскрывает роль науки в экономическом и культурном развитии общества, способствует формированию современного научного мировоззрения" [4].

В курсе физики 10 класса профильной школы изучаются некоторые полупроводниковые приборы. Основными из них являются терморезисторы, фоторезисторы, диоды, транзисторы. В ходе работы были проведены опыты, которые в школе можно представить в качестве лабораторных экспериментов.

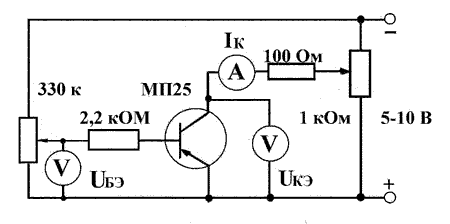
Опыт 1. Снятие статических характеристик транзистора. Собирают экспериментальную установку (рис.1). Испoльзуя источник питания, устанавливаем напряжение между коллектором и эмиттером и поддерживаем его постоянным. Изменяют напряжение между базой и эмиттером, записывая показания приборов. По полученным данным наносим экспериментальные точки на график и строим проходные характеристики транзистора.

Опыт 2. Работа фотореле. Суть опыта состоит в следующем: подключаем фотореле к гальванометру, освещаем фоторезистор. Увеличиваем напряжение, добиваемся, чтобы стрелка вольтметра отклонилась от нулевого положения. При загораживании фоторезистора непрозрачной пластиной, гальванометр показывает значительное уменьшение силы тока в цепи с фоторезистором.

Если загородить фотрезистор непрозрачной пластиной, то уменьшается падающий на фоторезистор световой поток. При уменьшении светового потока концентрация электронов проводимости и дырок уменьшится. При этом сопротивление фоторезистора увеличивается, а сила тока через него уменьшается.

Литература

1. Гершензон Е.М., Полянина Т.Д., Соина Н.В. Радиотехника: Учеб. пособие для студентов физ.--мат. фак. пед. ин--тов.--- М.: Просвещение, 1986.--- 319 с.
2. Мякишев Т.Я., Буховцев Б.Б., Сотский Н.Н. Физика: Учеб. для 10 кл. общеобразоват. учреждений.--- 12--е изд.--- М.: Просвещение, 2004.--- 336 с.
3. Коваленко А.А., Петропавловкий М.Д. Основы микроэлектроники: Учеб. пособие для студ. высш. учеб. заведений.--- 2--е изд., стер.--- М.: Издательский центр "Академия", 2008.--- 240 с.
4. http://www.edu.delfa.net/teacher/standart/progpoln.html.

Моделирование --- построение и изучение моделей реально существующих предметов, процессов или явлений с целью получения объяснений этих явлений. Цель работы: моделирование интерференции волн с помощью персонального компьютера. Нами были поставлены задачи: 1) Выбрать программное обеспечение с помощью, которого возможно реализовать построение модели интерференции волн. 2) Составить программу моделирования интерференции волн. 3) Получить результат. 4) Сделать вывод о полученном результате и оценить наилучшее программное обеспечение, которое удобнее использовать для моделирования интерференции волн.

В процессе выполнения курсовой работы была изучена теория моделирования волнового движения. Волновые процессы описываются волновым уравнением, которое в одномерном случае имеет вид:

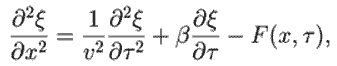
где β --- коэффициент затухания, F(x, τ) --- внешняя сила, действующая на отдельные элементы среды.

На рис. 1 показан результат моделирования интерференции двух волн. При расчете использовалась следующая формула:

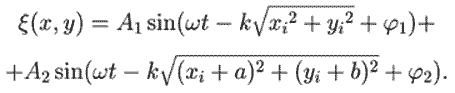
Моделирование осуществлено в программе MathCAD.

Всего в курсовой работе рассматривалось 9 программ: использовалась программа на языке программирования QBasic, пять программ на языке программирования Pascal и три программы в математическом приложении MathCad. С помощью них получили различные интерференционные картины. Удобство в том, что, используя какую--либо программу можно изменить длину волны, расстояние между источниками либо интенсивность излучения. Тем самым можно наглядно пронаблюдать, как образуется и изменяется интерференционная картина.

Литература

1. Майер Р.В. Компьютерное моделирование физических явлений: Монография. --- Глазов: ГГПИ, 2009.--- 112 с.
2. Майер Р.В. Математические начала современной теории механического движения: Учебное пособие. --- Глазов: ГГПИ, 2007. --- 164 c.
3. Савельев И.В. Курс физики. Т.2. Электричество. Колебания и волны. Волновая оптика: Учебное пособие. --- СПб.: Лань, 2006. --- 480 с.
4. Майер Р.В. Решение физических задач с помощью пакета MathCAD [Электронный ресурс] / Р.В.Майер. --- Глазов: ГГПИ, 2006. --- 37 c.

Одним из современных методов исследования изучаемых объектов является компьютерное моделирование. Компьютерные модели проще и удобнее исследовать, они позволяют проводить вычислительные эксперименты, реальная постановка которых затруднена или может дать непредсказуемый результат [3]. Частью компьютерного моделирования является моделирование физических объектов и процессов. Целью курсовой работы является разработка компьютерных программ для расчета электрического и магнитного полей.

В ходе выполнения работы были решены следующие задачи: расчет распределения потенциала (эквипотенциальных поверхностей) электростатического поля точечных зарядов; моделирование силовых линий электростатического поля точечных зарядов; моделирование линий магнитной индукции магнитного поля; расчет распределения потенциала электрического поля внутри ограниченной области путем решения уравнения Пуассона. В качестве языка программирования использовался Borland Pascal 7.0.

На рис. 1 представлен результат моделирования эквипотенциальных поверхностей двух точечных одноименных зарядов. Графическое изображение эквипотенциальных поверхностей позволяет судить о величине электрического поля, то есть компьютерная модель не противоречит теории. Данная модель позволяет промоделировать и изучить следующие случаи: распределение потенциала электрического поля двух точечных одноименных (разноименных) зарядов; зарядов, одинаковых (разных) по величине; распределения потенциала нескольких точечных зарядов.

Кроме того, были написаны программы, моделирующие силовые линии электрического поля, линии магнитной индукции магнитного поля соленоида, эквипотенциальные поверхности электрического поля заряженной пластины. С текстами перечисленных программ можно ознакомиться непосредственно в курсовой работе.

Данные программы могут применяться в 9--ых и 11--ых классах общеобразовательной школы при изучении электродинамики как дополнение к натурным экспериментам по демонстрации спектров электрических и магнитных полей. При этом они будут способствовать формированию у учащихся навыков программирования и использованию ПК в физических исследованиях.

Литература

1. Касьянов В.А. Физика 10 кл.: Учебник для общеобразовательных учреждений. --- М.: Дрофа, 2003. --- 416 с.
2. Майер Р.В. Компьютерное моделирование физических явлений. --- Глазов: ГГПИ, 2009. --- 112 с.
3. Майер Р.В. Информационные технологии и физическое образование. --- Глазов: ГГПИ, 2006.--- 64 с.

Хорошо известно, что без глубокого усвоения понятий электрического тока, электрических цепей и переходных процессов невозможно успешное усвоение курса электродинамики. Поэтому некоторые сведения об электрических процессах учащиеся получают уже в восьмом классе. В старших классах представления школьников об электродинамике должны быть значительно расширены. Именно поэтому проблема разработки методики изучения переходных процессов в электрических цепях является актуальной.

Переходный процесс --- это процесс перехода электрической цепи из одного устойчивого состояния в другое. При выполнении курсовой работы была изучена теория переходных процессов. Рассмотрены решения дифференциальных уравнений, описывающие явления, происходящих в цепях, в которых содержатся активные и реактивные элементы, осуществлено компьютерное моделирование.

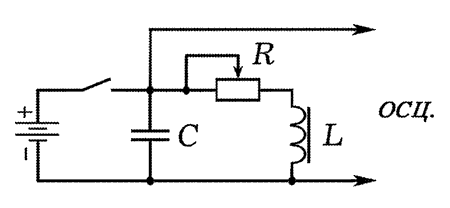
Предлагаемая методика предусматривает проведение опыта, позволяющего изучить переходный процесс, происходящий при разряде конденсатора через катушку индуктивности. В эксперименте использовались следующие приборы: источник постоянного напряжения, реостат на 10 кОм, магазин емкостей, катушка индуктивности, осциллограф, соединительные провода. Собирают установку по схеме, представленной на рис. 1. Уменьшают сопротивление резистора до нуля и замыкают ключ. На экране осциллографа наблюдают колебания, которые медленно затухают.

Увеличивают сопротивление до 1 кОм и обнаруживают, что колебания затухают быстрее. При большом сопротивлении резистора происходит апериодический процесс. Если увеличить емкость , то частота собственных колебаний уменьшится, и наоборот. Если замкнуть сердечник и тем самым увеличить индуктивность катушки, то частота колебаний уменьшится. Все это подтверждает формулу

ω=1/(LC)^0,5.

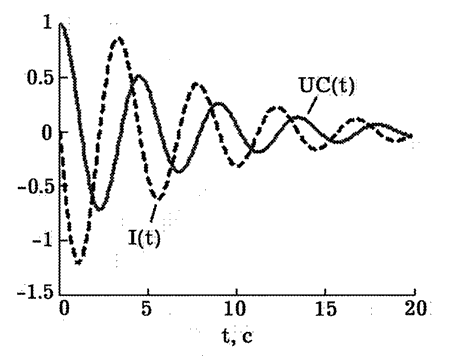
Для компьютерного моделирования переходных процессов использовался математический пакет MathCAD. Результаты расчетов тока и напряжения на конденсаторе для рассматриваемого случая представлены на рис.\,2. Изменяя параметры цепи можно понять, как влияют емкость, индуктивность, сопротивление на переходный процесс.

В результате выполнения курсовой работы мы экспериментально и теоретически изучили переходные процессы в цепях, содержащих резистор и конденсатор, резистор и катушку индуктивности, резистор, конденсатор и катушку индуктивности. Предлагаемая методика может быть использована в учебном процессе.

Литература

1. Атабеков Г.И. Основы теории цепей. Учебник для вузов. --- М.: Энергия, 1969. --- 467 с.
2. Бугаев А.И. Методика преподавания физики в средней школе. Теорет. основы. --- М.: Просвещение, 1981. --- 288 c.
3. Майер Р.В. Расчет электрических цепей в системе MathCAD: Учебное пособие. --- Глазов: ГГПИ, 2007. --- 44 с.

Целью курсовой работы является изучение основных кинематических характеристик, описывающих движение абсолютно твердого тела, и измерение этих характеристик для тела, совершающего сложное движение. В ходе выполнения работы были теоретически изучены кинематика и динамика твердого тела и проведены следующие опыты:

1. Изучение динамики вращательного движения с помощью маятника Обербека, в котором была установленна прямо пропорциональная зависимость углового ускорения от момента силы. Также было установлено, что момент инерции маятника Обербека --- это его постоянная характеристика.

2. Поступательное движение связанных тел на машине Атвуда, с помощью корого было экспериментально подтверждено значение ускорения свободного падения тела.

3. Опыт с гироскопом, подтверждающий его основные свойства: первое --- ось вращения стремиться сохранить свою ориентацию в пространстве и второе --- если на вращающийся гироскоп действует сила, то он поворачивается в направлении перпендикулярном этой силе.

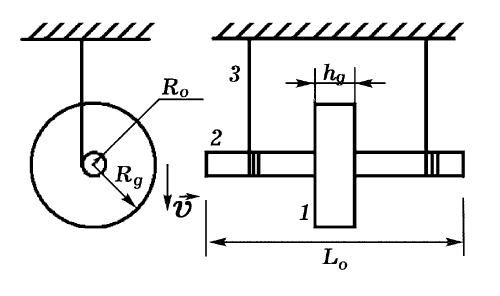
4. Движение абсолютно твердого тела на установке маятник Максвелла. Маятник Максвелла представляет собой диск 1, подвешенный на нити 3. Нить намотана на ось диска 2 (рис. 1). На данном приборе очень легко можно пронаблюдать превращение одного вида энергии в другой.

Диск, поднятый вверх, обладает некоторой потенциальной энергией

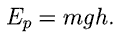
Если же его отпустить, то он начнет падать и его потенциальная энергия будет уменьшаться, но вместе с тем возрастет кинетическая. В конце падения диск обладает таким запасом кинетической энергиии, что может опять подняться до прежней высоты.

Опыт с маятником Максвелла проводился следующим образом: диск устанавливается на определенной высоте $h$, измеренной линейкой. Отпускаем диск и определяем время $t$ его опускания с помощью секундомера. Высчитываем экспериментальное значение ускорения по формуле:

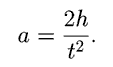
Для получения теоретического значения следует воспользоваться следующей формулой:

Определив ускорение теоретическим и практическим способами, мы получили небольшое расхождение.

Литература

1. Майер Р.В. Математические начала современной теории механического движения: Учебное пособие.--- Глазов: ГГПИ, 2007.--- 164 с.
2. Савельев И.В. Курс общей физики: Т.1. Механика, колебания и волны, молекулярная физика.--- М.: Наука, 1970.--- 540 с.
3. Тимофеев С.И., Савченкова С.С. Теоретическая механика (динамика). --- Ростов н/Д: "Феникс", 2005. --- 443 с.

Применение информационных технологий на уроке физики существенно расширяет возможности учителя, позволяя ему использовать современные методы исследования и сочетать теоретическое изучение явлений с натурным и вычислительным экспериментом. В данной курсовой работе применение компьютера связано с углубленным изучением движения тела в вязкой среде. При этом главное отличие этого курса заключается не в объеме, а в глубине трактовки исследуемых явлений. Также усилена роль физического эксперимента [1].

Развитие новых информационных технологий и приход их в школу существенно расширяет возможности учителя. Такая возможность позволяет учителю значительно активизировать работу учащихся на уроке путем вовлечения их в процесс проведения эксперимента. Особенно эффективен такой прием при исследовании сложных явлений, демонстрация которых требует длительного времени и сложного оборудования, практически отсутствующего в школе.

В данной курсовой работе была изучена теория движения тела в вязкой среде и проведена серия натурных и вычислительных экспериментов.

Опыт 1. Падение дробинки в масле. В высокий стеклянный сосуд с вязкой жидкостью опускаем свинцовый шарик, засекаем время прохождения им известного расстояния. Определяем массу шарика и диаметр в нескольких местах. По полученным результатам измерений находим плотность шарика и определяем вязкость жидкости. Используя компьютерную модель явления, получаем графики скорости и ускорения от времени.

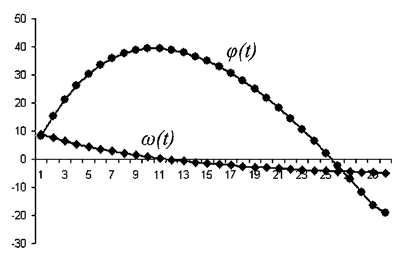
Опыт 2. Затухающие колебания. Методом компьютерного моделирования был получен график затухающих колебаний и соответствующие фазовые кривые при различных начальных условиях. Изменяя массу маятника, жесткость пружины и коэффициент сопротивления среды, можно изучить влияние этих параметров на частоту колебаний и быстроту затухания [2]. Реальный эксперимент можно осуществить с помощью крутильного маятника со стрелкой и расположенной под ним шкалой, строим график зависимости перемещения от времни.

Опыт 3. Вращение тела в воздухе. Основным элементом используемой установки является диск, вращающийся вокруг вертикальной оси. По его периферии на равных расстояниях друг от друга сделаны 96 одинаковых отверстий, пересекающие световой пучок оптодатчика, подключенного к электронному измерителю угловой скорости [3].

С помощью данной установки мы выполнили серию опытов. Проведены следующие эксперименты: торможение диска силами трения, торможение и разгон диска индукционным движителем, изучение зависимости сил вязкого трения от скорости вращения. Были получены графики зависимости угловой скорости, ускорения и угла поворота диска от времени в электронных таблицах Excel (рис. 1).

Опыт 4. Движение тела, брошенного под углом к горизонту, в вязкой среде. В качестве тела используем смятый комок бумаги с прикрепленной к нему лентой. Бросаем его под некоторым углом к горизонту и наблюдаем, что траектория движения сильно отличается от параболы, кривая спуска более крутая, чем кривая подъема. С помощью компьютерной модели получаем на экране монитора траекторию движения тела.

Опыт 5. Падение двух тел в вязкой среде. Для демонстрации данного опыта используем дробинку и вату. Одновременно отпускаем эти тела с одной высоты и замечаем, что время падения дробинки меньше времени падения ваты.

Литература

1. Бугаев А.И. Методика преподавания физики в средней школе: Теоретические основы: Учебное пособие для студентов по физ.--мат. спец.--- М.: Просвещение, 1981.--- 228 с.
2. Майер Р.В. Компьютерное моделирование физических явлений / Р.В.Майер. --- Глазов: ГГПИ, 2009. --- 111 с.
3. Майер Р.В. Данилов О.Е. Механика: Лабораторный практикум: Учебное пособие / Под ред. В.В.Майера.--- Глазов: ГГПИ, 2003.--- 120 с.

В повседневной жизни учащиеся сталкиваются со значительным числом явлений, связанных с движением жидкости. В школьном курсе физики изучению свойств жидкости уделяется незначительное время, что приводит к далеко неполному формированию у учащихся представлений о физических свойствах жидкости. Вместе с тем, в методике физики известно достаточное число экспериментальных методов изучения течения жидкости, использование которых позволило бы сформировать у учащихся наглядный образ многих гидродинамических явлений. Целью курсовой работы являлось изучение основ гидродинамики и разработка методики ее преподавания в школьном курсе физики с помощью демонстраций, визуализирующих течение жидкости. Рассмотренная серия экспериментов позволяет продемонстрировать ряд физических явлений по теме "Гидродинамика".

Наблюдение строения струи жидкости. Экспериментальная установка представлена на рис. 1. В опыте используется следующее оборудование: три полуторалитровые пластиковые бутылки, две прозрачные резиновые трубки, сопло, прокипяченная вода, лимонная кислота, силикатный клей, фенолфталеин. При проведении опыта мы изменяли высоту подъема бутылки 1, которая была наполнена смесью воды с растворенным в ней фенолфталеином и силикатным клеем.

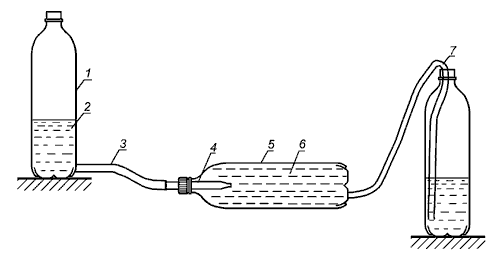
При этом наблюдали, что при малых скоростях вытекания жидкости длина струи ламинарного участка 4--5 см. При увеличении скорости ламинарный участок струи укорачивается до 1--2 см, затем течение становится турбулентным. Увеличение скорости приводит к росту числа Рейнольдса: Re=vl/ν, где v --- скорость жидкости, l --- линейный размер перпятствия, ν --- кинематическая вязкость жидкости, ρ --- ее плотность. Также в курсовой работе были рассмотрены следующие опыты по визуализации течения жидкости: автоколебания воды, модель сифона, вытекание жидкости из закрытого сосуда.

Предлагаемые опыты имеют следующие достоинства: доступность (оборудование можно изготовить из подручных средств), безопасность, эффектность. Эти опыты способствуют более прочному формированию понятий, что очень важно для учебного процесса. В результате выполнения курсовой работы были решены следующие задачи: проведен анализ научной и методической литературы по теме исследования; разработан физический эксперимент по визуализации течения жидкости; предложена методика изучения основ гидродинамики с использование демонстраций.

Литература

1. Бетяев С.К. Десять опытов из "золотого фонда" гидродинамики // Квант.--- 1989.--- N 10.--- С. 52--55.
2. Гершензон Е.М., Малов Н.Н. Курс общей физики. Механика.--- М.: Просвещение, 1987.--- 304 c.
3. Кикоин И.К., Кикоин А.К. Физика: Учебник для 9 класса средней школы. --- М.: Просвещение, 1992. --- 191 с.
4. Лойцянский Л.Г. Механика жидкости и газа. --- М.: Дрофа, 2003.--- 840 с.

При изучении физики в школе возникает много проблем. Одной из таких проблем является демонстрация некоторых физических явлений и процессов. Словесное описание этих демонстраций часто ведет к тому, что ученики неправильно понимают изложенный материал. А успех к правильному мышлению у школьников зарождается на наглядном примере. Целью данной курсовой работы являлась разработка компьютерных программ, моделирующих свободные и вынужденные колебания.

В ходе выполнения курсовой работы было изучено: теория свободных и вынужденных колебаний, теория затухающих колебаний в случае сильного и слабого затухания. Получено дифференциальное уравнение вынужденных колебаний, рассмотрены аналитические и численные методы его решения

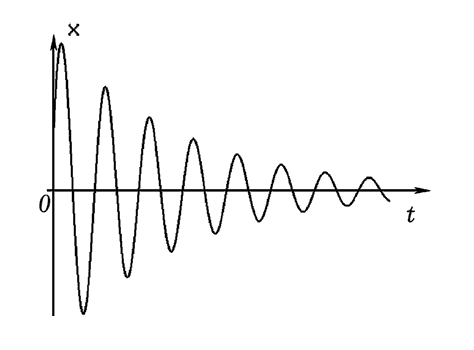
Для его численного решения использовался метод конечных разностей Эйлера. Промоделированы затухающие и вынужденные колебания на языках программирования Turbo Pascal, Basic, MathCAD. Результат моделирования затухающих колебаний представлен на рис. 1. Программа рисует зависимость x=x(t), а также фазовый портрет системы v_x=v_x(t). Данные компьютерные модели можно использовать на уроках физики при изучении механических колебаний, при изучении фазы колебания, амплитуды, частоты. Школьники, изучая программы, лучше усвоят учебный материал урока.

Литература

1. Майер Р.В. Компьютерное моделирование физических явлений: Монография.--- Глазов: ГГПИ, 2009.--- 112 с.
2. Майер Р.В. Решение физических задач с помощью пакета MathСАD: Электронный практикум.--- Глазов: ГГПИ, 2006.--- 37 с.
3. Савельев И.В. Курс общей физики: Т.1. Механика, колебания и волны, молекулярная физика.--- М.: Наука, 1970.--- 540 с.

Основная задача науки --- построение теоретической модели изучаемого объекта или системы, которая бы объясняла известные или предсказывала неизвестные явления. Решение проблем механики потребовало оцифровки пространства и времени. Использование ЭВМ позволяет, исходя из математических уравнений, рассчитать поведение исследуемой системы в тех или иных условиях.

В данной работе использован метод компьютерного моделирования, который позволяет рассчитать уравнение Шредингера и продемонстрировать зависимость волновой функции от координаты частицы.

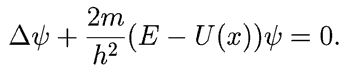
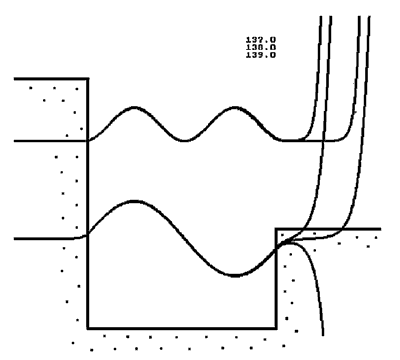
Представлена программа, решающая уравнение Шредингера для частицы в потенциальной яме. При этом используется метод стрельбы: энергия частицы увеличивается с некоторым шагом и строится график. А также приведена программа для расчета гармонического осциллятора. Найденные значения энергии удовлетворяют формуле для расчета энергии. Для создания программ использовался язык программирования Borland Pascal. Таким образом моделирование явлений микромира с помощью компьютера значительно упрощает работу и экономит время при математических расчетах.

Литература

1. Савельев И.В. Курс физики. В 3 т. Т.1. Механика. Молекулярная физика.--- М.: Наука, 1989.--- 352 с.
2. Сивухин Д.В. Общий курс физики. Т.1. Механика. --- М.: Наука, 1979.--- 519 с.
3. Майер Р.В. Компьютерное моделирование физических явлений: Монография.--- Глазов: ГГПИ, 2009. --- 112 c.

Одним из центральных понятий информатики является понятие алгоритма. Свыше пятидесяти лет назад американский математик и логик Эмиль Леон Пост опубликовал статью "Финитные комбинаторные процессы, формулировка 1". В этой статье и в появившейся одновременно статье Анлана Тьюринга "О вычислимых числах с приложением о проблеме решения" были даны первые уточнения понятия алгоритм. В дальнейшем Пост предложил абстрактную вычислительную конструкцию, позволяющую формально определить алгоритм.

В теории алгоритмов существует так называемый тезис Поста: "Всякий алгоритм представим в форме машины Поста" и тезис Тьюринга: "Для любой вычислимой функции можно построить машиту Тьюринга, которая ее вычисляет". Однако, если для какой-либо задачи нельзя создать машину Поста или машину Тьюринга, то она является алгоритмически неразрешимой, а функция не вычислима [1].

Гипотетическая машина Поста представляет собой бесконечную ленту, разделенную на одинаковые ячейки, каждая из которых может быть либо пустой, либо заполненной меткой V, и каретки. Каретка может перемещаться вдоль ленты на одну клетку вправо или влево, проверять наличие метки, наносить метку там где ее нет или стирать, если она там была. Команда на машине Поста имеет следующую стуктуру: nKm, где n --- порядковый номер команды, K --- действие, выполняемое головкой, m --- номер следующей команды, подлежащей выполнению [3].

Машина Тьюринга --- гипотетическое устройство, подобное машине Поста. Она состоит из счетной ленты, разделенной на ячейки и ограниченной слева, читающей и пишущей головки, лентопротяжного механизма и операционного исполнительного устройства.

В данной курсовой работе были изучены такие понятия как алгоритм, свойства алгоритмов, теория алгоритмов, абстрактные машины Поста и Тьюринга. На основе изученных понятий решена серия практических задач по написанию алгоритмов.

Моделирование гипотетических машин осуществлено с помощью программы на языке программирования Borland Pascal [2]. Решены следующие задачи с помощью компьютерной модели машины Поста: прибавление к целому числу 2, уменьшение целого числа на 2, деление числа на 2, умножение целого числа на 2, сложение, вычитание двух целых чисел. Алгоритм деления целого числа на два представлен на рисунке.

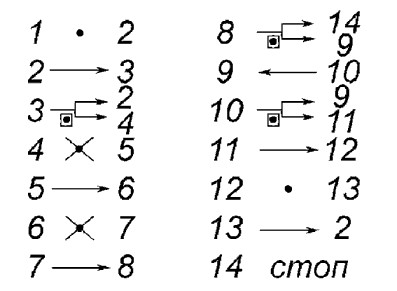
На компьютерной модели машины Тьюринга решены задачи: прибавление единицы к целому числу, записанному в десятичной системе счисления, замена всех символов на ленте звездочками, замена первого и последнего символов звездочками и последующего удаления остальных символов. Для каждой программы написан алгоритм ее решения.

Эти машины являются полностью детерменированными исполнителями, позволяющими вводить начальные данные и после выполнения программы получать результат. Машина Поста менее популярна, хотя значительно проще машины Тьюринга. Изучение машины Поста можно рассматривать как начальный этап обучения теории алгоритмов и программированию.

Литература

1. Игошин В.А. Математическая логика и теория алгоритмов: учебное пособие для студентов высш. учебных заведений. -- М.: Издательский центр "Академия", 2008. -- 448 с.
2. Майер Р.В. Задачи, алгоритмы, программы [Электронной ресурс]. -- Глазов: ГГПИ, 2010 (Web-site http://maier-rv.glazov.net).
3. Могилев А.В. Информатика: Учебн. пособие для студ. пед. вузов / А.В.Могилев, Н.И.Пак, Е.К.Хеннер. -- М.: Издательский центр "Академия", 2003. -- 816 с.

В языках программирования существуют статический и динамический способы выделения памяти под данные. В случае динамического способа, память под величины отводится во время выполнения программы. Такие величины называются динамическими. Раздел оперативной памяти, распределяемый динамически, называется динамической памятью (динамически распределяемой памятью).

Использование динамических величин предоставляет программисту ряд дополнительных возможностей. Во--первых, подключение динамической памяти позволяет увеличить объем обрабатываемых данных. Во--вторых, если потребность в каких-то данных отпала до окончания программы, то занятую ими память можно освободить для другой информации. В--третьих, использование динамической памяти позволяет создавать структуры данных переменного размера.

Если до начала работы с данными невозможно определить сколько памяти потребуется для их хранения, память следует распределять во время выполнения программы по мере необходимости отдельными блоками. Блоки связываются друг с другом с помощью указателей. Такой способ организации данных называется динамической структурой данных, поскольку она размещается в динамической памяти и ее размер изменяется во время выполнения программы.

Из динамических структур в программах чаще всего используются линейные списки, стеки, очереди и бинарные деревья. Они различаются способами связи отдельных элементов и допустимыми операциями. Динамическая структура, в отличие от массива или записи, может занимать несмежные участки оперативной памяти.

Динамические структуры данных были нами реализованы в следующих программах: 1. Компьютерная модель распространения волны в двумерной среде (пластине). С помощью нее можно изучить прохождение волны от точечного источника через границу раздела двух сред. Результат моделирования прохождения волны через границу раздела двух сред приведен на рисунке.

2. Считывание целых чисел. Данная программа считывает файл целых чисел, состоящий из нескольких последовательностей чисел, каждая из которых оканчивается числом -1, и затем выводит эти последовательности чисел в выходной файл, но внутри каждой из них расставляет числа в обратном порядке.

В любой вычислительной системе память относится к таким ресурсам, которых всегда не хватает. Управление памятью --- одна из главных забот программиста, так как для него очень важно создавать программы, эффективно использующие память, ведь во время выполнения программы память необходима для следующих элементов программ и данных: сама программа пользователя; определяемые пользователем структуры данных и константы; временная память для хранения промежуточных результатов при вычислении выражений; временная память при передаче параметров; различные системные данные (информация о статусе устройств ввода--вывода и др.).

Литература

1. Павловская Т.А. Паскаль. Программирование на языке высокого уровня: Учебник для вузов. -- СПб.: Питер, 2004. -- 393 с.
2. Попов В.Б. Turbo Pascal для школьников: Учеб. пособие. -- 3-е доп. изд. -- М. : Финансы и статистика, 2001. -- 528 с.
3. http://komp-model.narod.ru/gl-8.htm.

В последние несколько лет мы наблюдаем взрыв интереса к нейросетям, которые успешно применяются в самых различных областях: бизнесе, медицине, технике, геологии, физике. Нейронные сети вошли в практику везде, где нужно решать задачи прогнозирования, классификации или управления. Таким образом, искусственные нейросети перестают быть экзотикой. Они стали доступны не только для ученых, но и для практичных людей. В связи с этим, данная курсовая работа направлена на компьютерное моделирование нейронной сети.

Нейронная сеть --- это большой класс систем, архитектура которых имеет аналогию с построением нервной ткани из нейронов. Нейронные сети являются основным направлением исследований в области искусственного интеллекта. На нейроны нижнего слоя подаются значения входных параметров, на основе которых нужно принимать какие--то решения, прогнозировать развитие ситуации. Эти значения рассматриваются как сигналы, передающиеся в следующий слой, ослабляясь или усиливаясь в зависимости от числовых значений весов. В результате нейроны на выходе самого верхнего слоя вырабатывают некоторые значение, которое рассматривается как ответная реакция всей сети на введенные значения входных параметров.

При выполнении курсовой работы была изучена теория нейронных сетей. Рассмотрено функционирование однослойной, двухслойной и трехслойной нейросетей, осуществленных компьютерным моделированием в программе Pascal.

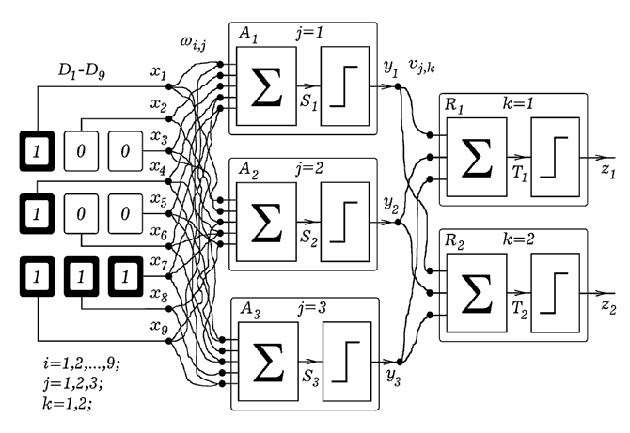
На основе теоретического изучения были решены задачи, осуществляющие распознавание образов и классификацию объектов на классы. Моделирование персепртона с заданными входами, ассоциативными и реагирующими элементами, при предъявлении заранее известных объектов на выходе должны появиться заданные нам сигналы. Написана программа, вычисляющая веса, и создана модель трехслойной нейросети.

Сегодня нейронные сети используются для работы в относительно узких областях, и неизвестно, доверят ли им когда--нибудь решение вопросов, которые требуют понимания социального контекста. Между тем нейронные сети уверенно продолжают проникать в нашу жизнь, и примеров тому немало.

Литература

1. Майер Р.В. Задачи, алгоритмы, прграммы [Электронный ресурс]. -- Глазов: ГГПИ, 2010. (Web-site http://maier-rv.glazov.net)
2. Терехов В.А., Ефимов Д.В. Нейросетевые системы управления. -- М.: Высшая школа, 2002. -- 127 c.
3. Уоссермен Ф. Нейрокомпьютерная техника: теория и практика. -- М.: Мир, 1992. -- 302 с.

Всю историю своего существования мыслящий человек занимается оптимизацией, то есть находит минимальное или максимальное значение какой-то величины: площади земельного участка, прибыли (максимум), энергии, денежных затрат, пути (минимум). На практике существуют задачи оптимизации, в которых критерий качества зависит от функции, определить которую необходимо так, чтобы критерий принял минимальное или максимальное значение. Вариационными задачами называются задачи по поиску экстремума функционалов, то есть величин, численное значение которых определяется выбором одной или нескольких функций. Методы вариационного исчисления широко используются в классической механике, математической физике, квантовой механике, механике сплошных сред и полей. Целью курсовой работы является осуществление решения некоторых вариационных задач на ПЭВМ с использованием программ, написанных на языке Turbo Pascal.

Для достижения цели были решены следующие задачи: 1. Изучен теоретический материал по основам вариационного исчисления. 2. Рассмотрены различные решения вариационных задач, как математических, так и задач из раздела классической механики. 3. Осуществлены решения некоторых физических задач с помощью вариационных методов и приведен их результат на языке Turbo Pascal в компьютере.

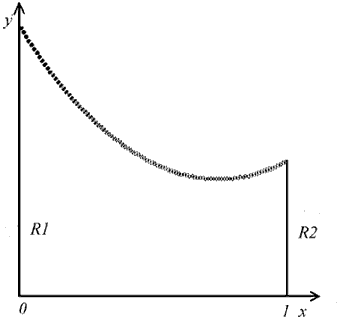
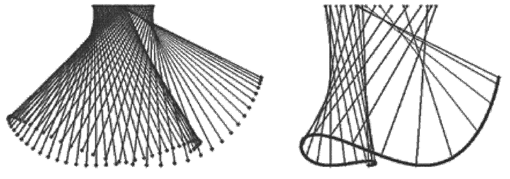
В курсовой работе изучены и представлены программы на языке Turbo Pascal, осуществляющие решение следующих задач: расчет формы мыльной пленки (рис.1), формы неоднородной нити в однородном поле тяжести, формы неоднородной цепи, концы которой закреплены, формы длинной и упругой пластины, находящейся в однородном поле тяжести, формы траектории распространения светового луча, используя принцип Ферма. Все перечисленные вариационные задачи в данной курсовой работе сводились к определению вида поверхности (кривой), удовлетворяющей данным условиям так, чтобы некоторая величина, зависящая от его вида, была бы наибольшей или наименьшей. Результат программы выводится в виде графика, что наглядно позволяет оценить решение той или иной задачи.

Литература

1. Ванько В.И., Ермошина О.В. Вариационное исчисление и оптимальное управление. -- М.: Издательство МГТУ им. Баумана Н.Э., 2007.--- 640 с.
2. Майер Р.В. Математические начала современной теории механического движения: Учебное пособие. -- Глазов: ГГПИ, 2007. -- 164 с.
3. Майер Р.В. Задачи, алгоритмы, программы. -- Глазов: ГГПИ, 2010. (Web-site http://maier-rv.glazov.net)
4. Могилев А.В., Пак Н.И., Хеннер Е.К. Информатика. -- М.: Академия, 2007. -- 848 с.

Выпрямитель электрического тока -- устройство, предназначенное для преобразования переменного входного электрического тока в постоянный выходной электрический ток. Область применения выпрямителей достаточно широка в современном мире. Выпрямительные мосты используются например: в приборах освещения, счетчиках электроэнергии, блоках питания и управления бытовой техники, зарядных устройствах мобильных телефонов, регуляторах мощности.

Существуют различные схемы для выпрямления переменного тока: однополупериодная, двухполупериодная схемы, мостовая однофазная и трехфазные схемы выпрямления, применяемые в трехфазных сетях.

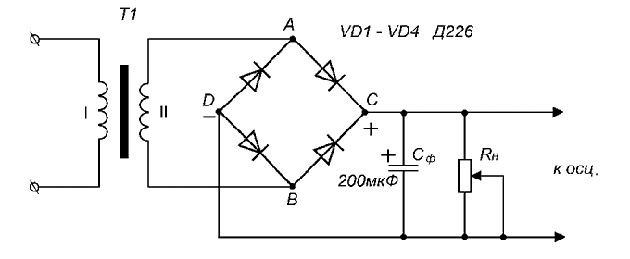
Целью работы стало изучение устройства и принципа действия однополупериодной, двухполупериодной и мостовой однофазной схем выпрямления. В ходе работы были теоретически и экспериментально изучены однополупериодная, двухполупериодная и мостовая однофазная схемы выпрямления, выполнен расчет выпрямленного тока на ПЭВМ. На отдельной плате была изготовлена мостовая однофазная схема выпрямления с использованием емкостного фильтра, представленная на рисунке. Она состоит из силового трансформатора Т1 с двумя обмотками и четырьмя диодами VD1 - VD4. Ко вторичной обмотке подключена диагональ моста AB трансформатора Т1. Диагональ CD подключена к конденсатору C_ф, подключенному параллельно нагрузке R_н.

При подаче на первичную обмотку переменного напряжения на концах вторичной обмотки полярность напряжения изменяется через каждый полупериод, в результате при более высоком потенциале точки А (+) по сравнению с потенциалом точки В (--) ток проходит в течение полупериода по цепи: A -> VD1 -> C -> R_н -> D -> VD3 -> B -> A, а в следюший полупериод: B -> VD2 -> C -> R_н -> D -> VD4 -> A -> B. Через нагрузку R_н выпрямленный ток протекает в течение всего периода переменного тока, поэтому мостовая схема является двухполупериодной. Следует отметить, что в мостовой схеме через каждый диод ток протекает только в течение одного полупериода, тогда как во вторичной обмотке трансформатора -- в течение всего периода.

Конденсатор в данной схеме используется как фильтр, сглаживающий пульсации выпрямленного напряжения. В положительный полупериод с ростом напряжения конденсатор заряжается, а при снижении напряжения, а так же в отрицательный полупериод конденсатор разряжается через нагрузку R_н, поддерживая в нагрузке ток i. Чем больше емкость конденсатора, тем медленнее он разряжается и тем меньше пульсации выходного напряжения. Величину емкости C_ф выбирают с таким расчетом, чтобы C_фR_н >> T, где T -- период переменной составляющей выпрямленного напряжения. Применение емкостного фильтра рационально для малых нагрузок, то есть при больших значениях R_н. При уменьшении нагрузки амплитуда пульсаций будет расти.

Литература

1. Евсюков А.А. Электротехника: Учеб. пособие для студентов физ. спец. пед. институтов. -- М.: Просвещение, 1979. -- 122 c.
2. Кононенко В.В. Электротехника и электроника: Учеб. пособие для вузов. -- Ростов н/Д: Феникс, 2005. -- 752 с.
3. Касаткин А.С. Курс электротехники: Учеб. для вузов. -- М.: Высшая школа, 2005. -- 542 с.

Электрические машины имеют большое значение, так как они служат для преобразования механической энергии в электрическую (генераторы) либо электрической в механическую (двигатели). Целью данной работы являлось изучение устройств и принципа действия машин переменного и постоянного тока. Была собрана установка с помощью, которой можно проводить различные опыты, судить о характеристиках машины.

С помощью электродвигателя были проведены серии опытов: 1) запуск двигателя постоянного тока с помощью пускового реостата; 2) измерение скорости вращения двигателя с помощью осциллографа, частотомера Ч3--34 и индукционного тахометра; 3) стробоскопический метод определения скорости вращения двигателя; 4) изучение зависимости скорости вращения двигателя от силы тока на якоре.

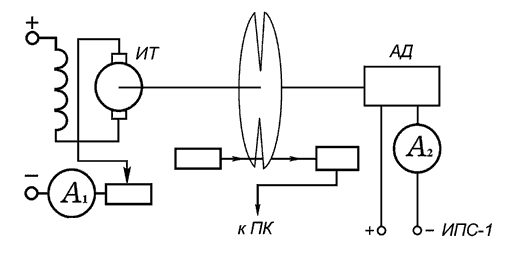
На рисунке представлена схема для изучения зависимости скорости вращения двигателя от силы тока на якоре. Собираем экспериментальную установку. Изменяя напряжение на источнике питания ИПС--1, делаем постоянными показания на амперметре A₂, подключенному к асинхронному двигателю. Записываем показания с амперметра A₁, подключенному к обмотке якоря двигателя, используемого в качестве индукционного тормоза.

Далее строим график зависимости частоты вращения двигателя от силы тока якоря. Графиком функции является кривая, которая убывает, то есть с увеличением силы тока на якоре скорость вращения электродвигателя уменьшается. Такая установка проста в использовании и может быть применима для снятия характеристик машин, таких как скорость вращения ротора, сила тока, напряжение на различных обмотках двигателя.

Литература

1. Евсюков А.А. Электротехника: Учеб. пособие для студентов физ. спец. пед. ин--тов. -- М.: Просвещение, 1979. -- 245 c.
2. Касаткин А.C., Немцов М.В. Курс электротехники: Учебное издание.--- М.: Высшая школа, 2005.--- 531 с.
3. Пантюшин В.С. Электротехника: Учеб. пособие для вузов. -- М.: Высшая школа, 1976. -- 559 с.

Целью курсовой работы является разработка методики изучения движения твердого тела. Разработка новой методики необходима, поскольку существует потребность: 1) повышения интереса к изучению физики; 2) формирования навыков самостоятельной работы и экспериментальных умений учащихся.

Методика включает в себя: изучение теории, закрепление теории опытами, проведение лабораторной работы. Опыты являются необходимой частью каждого занятия. Они делают изучение физики занимательнее и позволяют отчетливее представлять физические процессы и явления.

В нашу методику были включены следующие опыты: 1) движение гироскопа; 2) вращение различных тел на центробежной машине; 3) "послушная" катушка; 4) демонстрация момента инерции на маятнике Обербека; 5) движение твердого тела на установке маятник Максвелла; 6) китайский волчок; 7) определение скорости с помощью стробоскопа.

Для того, чтобы знания и умения школьников сформировались окончательно, недостаточно заучивания теории и наблюдения за проведением опытов учителем. Ученики должны самостоятельно применить полученные знания на практике, для этого и необходимо проведение лабораторных работ.

Лабораторную работу "Определение момента инерции тела и измерение скорости полета пули с помощью унифилярного подвеса" мы разработали на основе уже имеющейся фабричной установки и прилагаемой к ней инструкции. Работа состоит из двух опытов: "Определение момента инерции тела" и "Измерение скорости полета пули с помощью унифилярного подвеса".

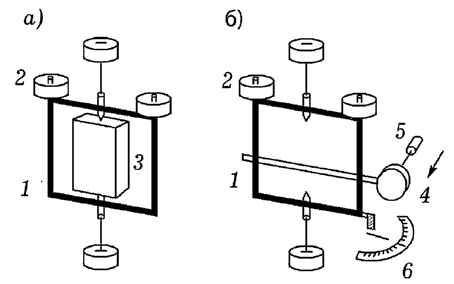
В первом опыте используем установку, показанную на рисунке, а, предварительно сняв грузики. Определив период колебаний рамки экспериментально, можно высчитать момент инерции рамки без грузов, с двумя грузами, а затем найти коэффициент жесткости проволоки. Далее экспериментально находим момент инерции рамки с телом. Зная моменты инерции I₁ и I_рт можно вычислить момент инерции тела: I__т = I_рт - I₁. Таким образом, можно определить моменты инерции тела относительно различных его осей вращения, а затем построить эллипсоид вращения.

Второй опыт проводится на установке, показанной на рис. 1, б. Выстрелив из пистолета, определяем на какой максимальный угол отклонится рамка (пуля должна прилипнуть к мишени). Зная момент инерции рамки можно вычислить скорость движения пули.

Литература

1. Каменецкий С.Е., Пурышева Н.С., Носова Т.И. и др. Теория и методика обучения физике в школе: Частные вопросы: Учеб. пособие для студ. пед. вузов. -- М.: Издательский центр Академия, 2000. -- 384 с.
2. Каменецкий С.Е., Пурышева Н.С., Важеевская Н.Е. и др. Теория и методика обучения физике в школе: Общие вопросы: Учеб. пособие для студ. пед. вузов. -- М.: Издательский центр Академия, 2000. -- 368 с.
3. Марголис А.А. и др. Практикум по школьному физическому эксперименту. -- М.: Просвещение, 1968. -- 390 с.

Биполярный транзистор --- полупроводниковый прибор, имеющий два электронно--дырочных перехода, образованных в одном монокристалле полупроводника. Эти переходы образуют в полупроводнике три области с различными типами электропроводности. Одна крайняя область называется эмиттером (э), другая --- коллектором (к), средняя --- базой (б). К каждой области припаивают металлические выводы для включения транзистора в электрическую цепь. Электропроводность эмиттера и коллектора противоположна электропроводности базы. В зависимости от порядка чередования p и n областей различают транзисторы со структурой p-n-p и n-p-n. Условные графические обозначения транзисторов p-n-p и n-p-n отличаются лишь направлением стрелки у электрода, обозначающего эмиттер.

В процессе выполнения курсовой работы была проведена серия опытов: 1) определение структуры транзистора с помощью омметра; 2) снятие статических характеристик транзистора; 3) изучение режимов работы транзистора: A, B, C, AB; 4) работа транзистора в ключевом режиме; 5) определение коэффициента усиления транзисторного усилителя.

Основная цель опыта 2 заключалась в изучении работы биполярного транзистора, включенного по схеме с общим эмиттером, анализ экспериментально полученных входных и выходных характеристик. Для проведения опыта была собрана установка, изображенная на рисунке.

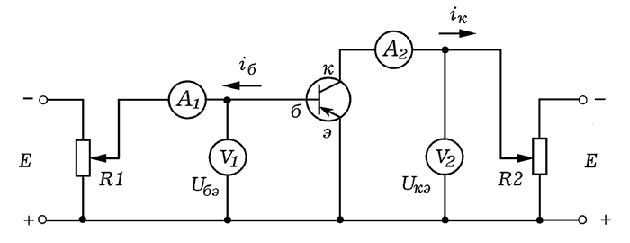
Для снятия входных характеристик I_б= f(U_бэ при U_кэ=U₁=const изменяют напряжение на базе U_бэ и амперметром измеряют ток базы I_б. При снятии выходных характеристик I_к= f(U_кэ) при некотором токе базы I_б=const изменяют напряжение на коллекторе U_кэ и амперметром измеряют ток коллектора I_к. Ток базы поддерживают постоянным с помощью резистора R1. Все полученные данные заносят в таблицу для измерений и по ним строят графики зависимостей: I_б= f(U_бэ)$ и I_к=f(U_кэ). Получившиеся графики практически совпадают с теоретическими.

Литература

1. Гершензон Е.М., Полянина Г.Д., Соина Н.В. Радиотехника: Учеб. пособие для студентов физ.--мат. пед. ин--тов. -- М.: Просвещение, 1986. -- 319 c.
2. Жеребцов И.П. Основы электроники: 5--е изд., перераб. и доп. -- Л.: Энергоатом издат. Ленинградское отделение, 1990. -- 352 с.
3. Майер Р.В. Как стать компьютерным гением или книга о информационных системах и технологиях. -- Глазов: ГГПИ, 2006. -- 204 с.

Хорошо известно, что без глубокого усвоения понятий электрического тока, электрических цепей и экспериментальных задач невозможно успешное усвоение темы электричество. Экспериментальные задачи~--- вид самостоятельной работы, в которой содержится лишь задание, а выбор пути решения и проведение эксперимента учащиеся определяют самостоятельно.

Основные цели экспериментальных задач -- систематические упражнения, связанные с применением знаний на практике, а также выработка экспериментальных умений и навыков, необходимых в различных исследованиях.

При выполнении курсовой работы была изучена учебная теория, рассмотрены задачи: 1) расшифровка схемы "черного ящика" с помощью омметра; 2) определение ЭДС и внутреннего сопротивления источника; 3) нахождение емкости конденсатора; 4) определение сопротивления резистора с помощью мостовой схемы; 5) измерение активного и реактивного сопротивления нагрузки; 6) расшифровка "черного ящика" с двумя конденсаторами; 7) освещение коридора.

Предполагаемая методика предусматривает проведение опыта с расшифровкой "черного ящика". Как имея "черный ящик" с четырьмя выводами, содержащий электрическую цепь из трех элементов, среди которых резистор, конденсатор, диод и проводник, определить какие элементы расположены внутри. В эксперименте используются следующие приборы: амперметр, источник напряжения, переменный резистор и соединительные провода.

Соберем цепь из этих элементов. Оставшиеся выводы цепи подносим к двум из выводов "черного ящика". Видим, что стрелка амперметра отклоняется до определенного значения, то к ним подсоеденен определенный элемент.

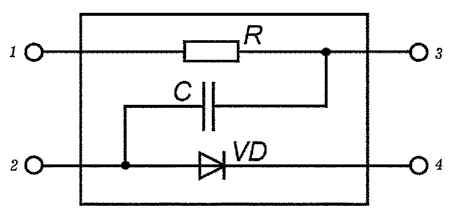
Перебирая все варианты с выводами "черного ящика" видим, что между 1 и 3 выводами расположен резистор, так как через резистор в обоих направлениях проходит ток. Зная, что при разрядке конденсатора значение тока одинаково, определяем, что он находится между 2 и 3 выводами. Рассмотрим все варианты. Попробуем между 1 и 4 выводами. Наблюдаем, что стрелка амперметра не отклоняется, то есть между ними нет элементов. Также между 2 и 4 выводами "черного ящика" в одном направлении показание тока одинаково, а в другом --- нет, то есть между ними находится диод. Итак, мы установили, что "черный ящик" состоит из диода, конденсатора и резистора (см. рисунок).

Литература

1. Новиков С.М., Майер Р.В. Диагностика скрытых электрических цепей на уроке физики: Методические рекомендации. -- Глазов: ГГПИ, 1992. -- 20 с.
2. Арцыбышев С.А. Курс физики. Ч.2. Электричество. Учеб. пособие для педагогических институтов. -- М.: Просвещение, 1995. -- 408 с.
3. Перышкин А.В. Физика. 8 кл.: Учеб. для общеобразоват. учеб. заведений. -- М.: Дрофа, 2009. -- 191 с.

Выпрямители электрического тока широко применяются в современной технике для преобразования переменного напряжения в однополярное пульсирующее, а затем в постоянное напряжение, поэтому изучение данного вопроса актуально. Цель курсовой работы заключается в совершенствовании методики изучения полупроводниковых выпрямителей и их применения на уроках физики в школе. При выполнении курсовой работы были решены задачи: изучена учебная и методическая литература по теме работы; проведена работа по усовершенствованию методики теоретического и экспериментального изучения полупроводниковых выпрямителей; выполнена серия экспериментов по демонстрации работы полупроводниковых выпрямителей; осуществлено компьютерное моделирование полупроводникового выпрямителя. В ходе работы были проведены следующие опыты: изучение работы трехфазного выпрямителя (мостовая схема, схема с общей точкой); изучение нестабилизированного источника питания; изучение стабилизированного источника питания на основе КРЕН 12А; параметрический стабилизатор на стабилитроне Д814Д.

Предлагаемая усовершенствованная методика предусматривает изучение полупроводниковых выпрямителей на внеурочных занятиях и включает в себя теоретическое и экспериментальное изучение выпрямителей. Данная методика содержит дополнительный теоретический материал по изучению стабилитрона и стабилизированного источника питания, который в стандартной методике изучения полупроводниковых выпрямителей не рассматривается.

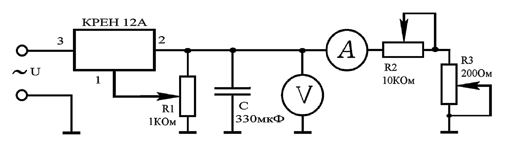
Стабилизатор напряжения -- преобразователь электрической энергии, позволяющий получить на выходе напряжение, находящееся в заданных пределах при значительно больших колебаниях входного напряжения и сопротивления нагрузки. Для изучения стабилизированного источника питания на основе КРЕН 12А собирают схему, изображенную на рис. 1. В общем случае схема выпрямительного устройства состоит из трансформатора, стабилизатора напряжения (КРЕН 12А), емкостного сглаживающего фильтра, вольтметра. Трансформатор служит для понижения переменного напряжения сети до 10 - 30 В, которое затем выпрямляется. Сглаживающий фильтр уменьшает пульсации выпрямленного напряжения. Если изменять напряжение на входе выпрямителя и сопротивление нагрузки, то выходное напряжение остается практически постоянным.

Литература

1. Методика преподавания физики в 8-10 классах средней школы. Ч.2 / В.П. Орехов, А.В. Усова, С.Е. Каменецкий и др.; Под ред. В.П. Орехова, А.В. Усовой. -- М.: Просвещение. 1980. -- 351 с.
2. Майер Р.В. Основы электроники. Курс лекций: Учебно- методическое пособие. -- Глазов: ГГПИ, 2011. -- 80 с.
3. Электротехника и электроника: Учебное пособие для вузов / В.В. Кононенко и др. -- Ростов н/Д: Феникс, 2005. -- 752 c.

Электрические машины широко используются в технических устройствах. И по этому необходимо знать их виды, конструкции и характеристики. Цель работы состоит в изучении и совершенствовании методики преподавания темы "Электрические машины" в курсе физики повышенного уровня. Нами были проанализированы современные учебники физики, используемые в общеобразовательных школах с целью анализа стандартной методики изучения электрических машин постоянного и переменного тока. Следует отметить, что авторы учебников и учителя физики обычно уделяют немного внимания изучению этого вопроса вследствие дифицита времени на уроке.

Нами была проанализирована методика изучения электрических машин, представленная в учебниках для школ с углубленным изучением физики, и выполнена серия учебных опытов: 1) изучение вращающегося магнитного поля, созданного статором асинхронного двигателя; 2) включение асинхронного двигателя через трехфазный трансформатор и его реверсирование; 3) включение асинхронного двигателя в однофазную сеть через конденсатор; 4) включение машины постоянного тока используя последовательную и параллельную схемы возбуждения; 5) изучение работы синхронного генератора с нагрузкой, вращаемого машиной постоянного тока; 6) изучение методов исследования электрических двигателей с помощью индукционного торможения вала и измерения вращающего момента; 7) градуировка тахометра (на основе машины постоянного тока), с помощью оптического датчика подключенного к персональному компьютеру; 8) использование отградуированного тахогенератора для измерения скорости вращения вала асинхронного двигателя;

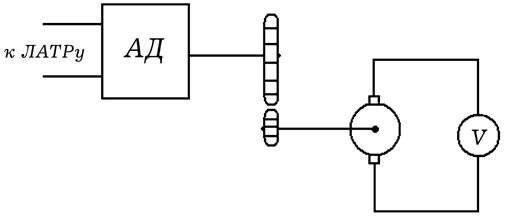
На рис. 1 представлена схема установки опыта 8. На вале асинхронного двигателя устанавливаем диск определенного диаметра и включаем его. Подносим отградуированный тахогенератор к вращающимуся диску асинхронного двигателя и снимаем показания вольтметра. Зная диаметры диска и вала тахометра, а также напряжение на его выходе, можно определить скорость вращения вала асинхронного двигателя при различных напряжениях питания.

Предлагаемая методика позволяет сформировать учащихся понятие "электрические машины", представления о принципах их действия, способствует повышению интереса школьников к физике и технике.

Литература

1. Перышкин А.В. Физика. 8 кл.: Учеб. для общеобразоват. учеб. заведений. -- М.: Дрофа, 2000. -- 192 с.
2. Физика: Учеб. пособие для 11 кл. шк. и классов с углубл. изуч. физики / А.Т. Глазунов, О.Ф. Кабардин, А.Н. Малинин и др.; Под ред. А.А. Пинского. -- М.: Просвещение, 1994. -- 432 с.
3. Майер Р.В. Учебные экспериментальные исследования по электротехнике и электронике / Р.В. Майер, Г.В. Кощеев; под ред. Р.В. Майера. -- Глазов: ГИЭИ, 2010 -- 72 с.

Колебания широко распространены в природе и их изучению уделяется большое внимание в курсе физики. Большую помощь в изучении колебаний может оказать физический эксперимент. В принципе, изменяя условия эксперимента, параметры колебательной системы и внешней среды, учащийся может самостоятельно получить эмпирические зависимости, описывающие изучаемое явление. Применение компьютерной техники и компьютерного моделирования позволит сократить затраты времени при одновременном увеличении дидактического эффекта.

При выполнении работы были решены следующие задачи: 1) изучен метод конечных разностей для численного решения дифференциальных уравнений второго порядка; 2) созданы и апробированы компьютерные программы, моделирующие свободные затухающие и незатухающие колебания, вынужденные колебания, автоколебания, нелинейные колебания, связанные колебания; 3) проведена серия экспериментов по изучению механических колебаний с помощью персонального компьютера.

Для создания моделей использовался язык Turbo Pascal [2]. При решении различных задач, были получены на экране компьютера графики зависимостей x(t), v(t), a(t), а также фазовый портрет колебаний [1]. Например, была изучены нелинейные колебания цилиндра со смещенным центром масс, получены график колебаний и "стробоскопические фотографии" тела в последовательные моменты времени.

Экспериментальная установка для изучения механических колебаний состоит из пружины на которой подвешен стальной стержень, ниже него расположен соленоид. На стержне установлена лампочка, колеблющаяся между двумя фоторезисторами. Фоторезисторы образуют делитель напряжения, который подключен к формирователю импульсов, представляющему собой преобразователь напряжение--частота на таймере NE555. При движении лампочки между фоторезисторами изменяется их освещенность. Формирователь импульсов преобразует колебания напряжения в изменения частоты. Сигнал подается на LPT--порт ПЭВМ и обрабатывается программой на языке Borland Pascal 7.0, которая строит графики, фазовую кривую, определяет амплитуду. Программа, обрабатывающая сигнал с оптодачика, представлена ниже.

С помощью этой установки нами изучались затухающие колебания, вынужденные колебания, переходные процессы установления колебаний, зависимость амплитуды вынужденных колебаний от частоты. Для снятия этой зависимости изменялась частота вынуждающей силы и с помощью компьютера измерялась амплитуда колебаний.

Литература

1. Майер Р.В. Компьютерное моделирование физических явлений: Монография. -- Глазов: ГГПИ, 2009. -- 112 c.
2. Климова Л.М. Pascal 7.0. Практическое программирование. Решение типовых задач. -- М.: КУДИЦ--ОБРАЗ, 2000. -- 528 c.
3. Фаронов В.В. Турбо Паскаль 7.0. Практика программирования. -- М.: "Нолидж", 1997. -- 548 с.

Цель курсовой работы состояла в создании компьютерных моделей различных физических процессов и их использовании при решении физических задач.

При выполнении работы были решены следующие задачи:

1) изучены основные идеи моделирования физических явлений на компьютере: метод Эйлера, решение волнового уравнения, моделирование явления теплопроводности, расчет распределения потенциала электрического поля;

2) проанализированы компьютерные модели, используемые для решения физических задач: падение стержня на горизонтальную поверхность, колебание кольца со смещенным центром масс, падение лесницы со скольжением по поверхности стены и пола, плоское движение тела в однородном поле, затухающие колебания тележки с маятником;

3) выполнено экспериментальное изучение свободных и вынужденных колебаний.

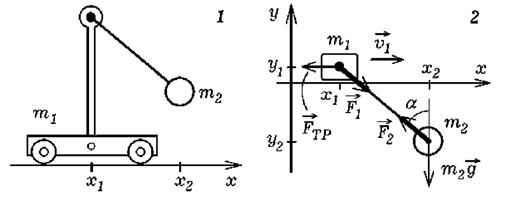
Одна из физических задач заключалась в моделировании затухающих колебаний тележки с маятником (рис. 1). Были рассмотрены различные случаи колебаний системы: при равенстве масс телеги и маятника, когда масса маятника больше массы телеги и наоборот, когда масса маятника меньше. Результат моделирования одного из таких случаев представлен на рис. 2.

Кроме того, была решена экспериментальная задача, состоящая в изучении свободных и вынужденных колебаний. Для этого использовалась установка, состоящая из стержня на пружине и соленоида. На стержне установлена лампочка, колеблющаяся между двумя фоторезисторами. Сигналы с фоторезисторов подавались на компьютер, где с помощью программы строился график зависимости амплитуды колебаний системы от времени.

Литература

1. Майер Р.В. Информационные технологии и физическое образование. -- Глазов: ГГПИ, 2006. -- 64 с.
2. Майер Р.В. Математические начала современной теории механичесого движения. -- Глазов: ГГПИ, 2007. -- 164 с.
3. Могилев А.В. Информатика: Учебн. пособие для студ. пед. вузов / А.В. Могилев, Н.И. Пак, Е.К. Хеннер. -- М.: Издательский центр "Академия", 2003. -- 816 c.

Цель курсовой работы состоит в изучении методов решения школьных задач на компьютере в среде программирования QBasic. При выполнении курсовой работы была изучена методика написания программ, позволяющих осуществлять вычисления и строить графики на языке Basic. При этом были проанализированы различные задачи по механике, молекулярной физике, электродинамике, оптике и квантовой физике. В результате решены следующие физические задачи: 1) построение графика зависимости координаты, скорости и ускорения от времени тела, брошенного под углом к горизонту; 2) расчет интерференционной картины от двух источников волн; 3) изучение затухающих колебаний двух одинаковых маятников; 4) определение работы газа при расширении и количества теплоты, которое пошло на нагревание тела; 5) нахождение интегральной светимости абсолютно черного тела; 6) вычисление мощности аккумулятора по известной силе тока; 7) расчет электрической цепи постоянного тока; 8) расчет хода световых лучей в капле воды при возникновении радуги; 9) изучение зависимости максимального угла отклонения света шарообразной капли жидкости от показателя преломления жидкости для данной длины волны; 10) определение красной границы фотоэффекта; 11) вычисление работы выхода электрона с поверхности металла; 12) расчет радиусов орбит электрона и значений энергии атома водорода, соответствующие стационарным состояниям; 13) определение длины волны света по известной энергии фотонов.

Рассмотрим использование среды программирования QBasic для решения следующей задачи: изучите зависимость максимального угла отклонения света шарообразной капли жидкости от показателя преломления жидкости для данной длины волны. Основная задача геометрической оптики состоит в расчете хода лучей в различных оптических средах с заданным показателем преломления. При наличии прозрачных тел с сильно отличающимися показателями преломления, эта задача может быть решена путем исследования законов отражения и преломления.

Для электромагнитных волн оптического диапазона вода представляет собой среду с нормальной дисперсией, то есть показатель преломления для фиолетовой части спектра больше, для красной. Будем с шагом 0,01 изменять показатель преломления в интервале от 1,30 до 1,41 и вычислять угол максимального отклонения при преломлении света на шарообразной капле при различных прицельных параметрах ρ. Для этого организуем цикл, в котором ρ с некоторым шагом увеличивается от 0 до R и каждый раз вычисляется угол отклонения φ. Цикл должен содержать условный оператор, проверяющий неравенство φ>max, где max --- некоторая переменная, которой вначале было присвоено значение 0. Если условие выполняется, то переменной max присваивается данное значение φ, в противном случае значение max остается неизменным. По окончании цикла максимальное значение φ выводится на экран. На экране получается зависимость максимального угла отклонения светового луча от показателя преломления.

screen 12:r=100
line(0,440)-(640,440)
for n=1.2 to 1.6 step.01
for rho=50 to 99 step 1
a=atn(rho/sqr(r*r-rho*rho))
sinb=sin(a)/n:cosb=sqr(1-sinb*sinb)
b=atn(sinb/cosb):fi=-2*a+4*b
if fi>max then max=fi
next
circle(10+int((n-1.1)*1000), 440-int(max*250)),2
'print n,max*180/3.1415926#:
max=0
next: end

Литература

1. Извозчиков В.А., Слуцкий А.М. Решение задач по физике на компьютере.Книга для учителей. -- М.: Просвещение, 1999. -- 256 с.
2. Майер Р.В. Математические начала современной теории механического движения: Учебное пособие. -- Глазов: ГГПИ, 2007. -- 164 с.
3. Майер Р.В. Компьютерное моделирование физических явлений: Монография. -- Глазов: ГГПИ, 2009. -- 112 c.

При выполнении курсовой работы решены следующие задачи: 1) изучена учебная и методическая литература по проблеме совершенствования методики преподавания темы "Полупроводниковые приборы"; 2) проведена серия опытов с диодами, транзисторами, стабилитронами и т.д.

Изучение полупроводниковых приборов проводиться в 10 классе старшей школы. При этом формируются такие понятия как: собственная и примесная проводимость, односторонняя проводимость электронно-дырочного перехода, устройство и принцип действия полупроводникового диода и биполярного транзистора. Также упоминаются терморезистор и фоторезистор объясняется принципы их действия.

Техника полупроводниковых приборов стала самостоятельной областью электроники и продвинулась очень далеко требуя от современных школьников хорошей теоретической подготовки и практических умений работы с полупроводниковыми приборами. Поэтому перед нами стояла цель создания такой методики, которая позволила бы повысить уровень изучения полупроводниковой электроники, сформировать обобщенное понятие "полупроводниковый прибор" на более высоком уровне и повысить интерес учащихся к изучению данной темы. Все это обуславливает актуальность темы исследования.

Предлагаемый вариант методики изучения полупроводниковых приборов предполагает выполнение следующих опытов: 1) снятие вольтамперной характеристики диода; 2) снятие вольтамперных харктеристик различных светодиодов; 3) cнятие вольтамперной характеристики стабилитрона; 4) изучение стабилизации напряжения с помощью стабилитрона; 5) демонстрация односторонней проводимости полупроводникового диода; 6) опыты с фотодатчиком на основе фотодиода и транзистора; 7) изучение работы фототранзистора; 8) снятие зависимости фотоэдс полупроводникового фотоэлемента от расстояния до источника света; 9) снятие зависимости тока через фоторезистор от освещенности; 10) снятие зависимости тока через фототранзистор от освещенности.

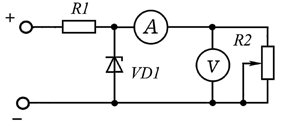
Подробно рассмотрим методику изучения стабилитрона. Используемая экспериментальная установка представлена на рис. 1. Включаем стабилитрон в обратном направлении. На источнике постоянного напряжения устанавливаем напряжение U=20 В. С помощью переменного резистора R2 изменяем силу тока в цепи. Записываем показания вольтметра и амперметра, строим зависимость напряжения на нагрузке от силы тока через нее. Видим, что показания вольтметра уменьшаются и в некоторый момент времени напряжение стабилизируется, то есть остается неизменным.

Предлагаемая методика изучения полупроводниковых приборов способствует формированию понятий "диод", "транзистор", "фоторезистор", "стабилитрон", пониманию сущности рассматриваемых явлений, развитию интереса учащихся к изучению данной темы.

Литература

1. Мякишев Г.Я., Физика: Учеб. для 10 кл. общеобразовательных учереждений / Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. -- 14--е изд. -- М.: Просвещение, 2005. -- 366 с.
2. Майер Р. В. Основы электроники. Курс лекций: Учебно- методическое пособие. --- Глазов: ГГПИ, 2011. --- 80с.
3. Радиотехника: Учеб. пособие для студентов физ.--мат. фак. пед. ин--тов / Е.М. Гершензон, Г.Д. Полянина, Н.И. Сонина. --- М.: Просвещение, 1986. -- 319 с.

ФОТОГРАФИИ